Introduction to Statistical Learning
with Applications in Python
7 Moving Beyond Linearity
So far in this book, we have mostly focused on linear models. Linear models are relatively simple to describe and implement, and have advantages over other approaches in terms of interpretation and inference. However, standard linear regression can have signifcant limitations in terms of predictive power. This is because the linearity assumption is almost always an approximation, and sometimes a poor one. In Chapter 6 we see that we can improve upon least squares using ridge regression, the lasso, principal components regression, and other techniques. In that setting, the improvement is obtained by reducing the complexity of the linear model, and hence the variance of the estimates. But we are still using a linear model, which can only be improved so far! In this chapter we relax the linearity assumption while still attempting to maintain as much interpretability as possible. We do this by examining very simple extensions of linear models like polynomial regression and step functions, as well as more sophisticated approaches such as splines, local regression, and generalized additive models.
- Polynomial regression extends the linear model by adding extra predictors, obtained by raising each of the original predictors to a power. For example, a cubic regression uses three variables, X, X2, and X3, as predictors. This approach provides a simple way to provide a nonlinear ft to data.
- Step functions cut the range of a variable into K distinct regions in order to produce a qualitative variable. This has the efect of ftting a piecewise constant function.
- Regression splines are more fexible than polynomials and step functions, and in fact are an extension of the two. They involve dividing the range of X into K distinct regions. Within each region, a polynomial function is ft to the data. However, these polynomials are
© Springer Nature Switzerland AG 2023
constrained so that they join smoothly at the region boundaries, or knots. Provided that the interval is divided into enough regions, this can produce an extremely fexible ft.
- Smoothing splines are similar to regression splines, but arise in a slightly diferent situation. Smoothing splines result from minimizing a residual sum of squares criterion subject to a smoothness penalty.
- Local regression is similar to splines, but difers in an important way. The regions are allowed to overlap, and indeed they do so in a very smooth way.
- Generalized additive models allow us to extend the methods above to deal with multiple predictors.
In Sections 7.1–7.6, we present a number of approaches for modeling the relationship between a response Y and a single predictor X in a fexible way. In Section 7.7, we show that these approaches can be seamlessly integrated in order to model a response Y as a function of several predictors X1,…,Xp.
7.1 Polynomial Regression
Historically, the standard way to extend linear regression to settings in which the relationship between the predictors and the response is nonlinear has been to replace the standard linear model
\[y\_i = \beta\_0 + \beta\_1 x\_i + \epsilon\_i\]
with a polynomial function
\[y\_i = \beta\_0 + \beta\_1 x\_i + \beta\_2 x\_i^2 + \beta\_3 x\_i^3 + \dots + \beta\_d x\_i^d + \epsilon\_i,\tag{7.1}\]
where ϵi is the error term. This approach is known as polynomial regression, polynomial regression and in fact we saw an example of this method in Section 3.3.2. For large enough degree d, a polynomial regression allows us to produce an extremely non-linear curve. Notice that the coefcients in (7.1) can be easily estimated using least squares linear regression because this is just a standard linear model with predictors xi, x2 i , x3 i ,…,xd i . Generally speaking, it is unusual to use d greater than 3 or 4 because for large values of d, the polynomial curve can become overly fexible and can take on some very strange shapes. This is especially true near the boundary of the X variable.
The left-hand panel in Figure 7.1 is a plot of wage against age for the Wage data set, which contains income and demographic information for males who reside in the central Atlantic region of the United States. We see the results of ftting a degree-4 polynomial using least squares (solid blue curve). Even though this is a linear regression model like any other, the individual coefcients are not of particular interest. Instead, we look at the entire ftted function across a grid of 63 values for age from 18 to 80 in order to understand the relationship between age and wage.
Degree−4 Polynomial
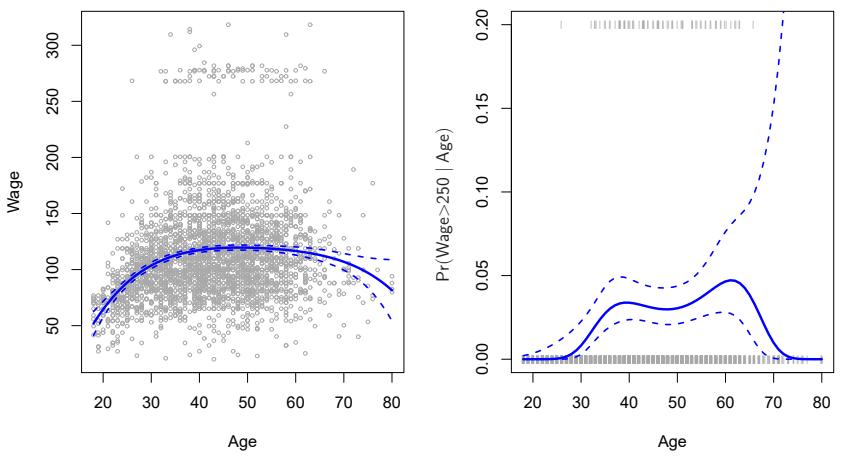
FIGURE 7.1. The Wage data. Left: The solid blue curve is a degree-4 polynomial of wage (in thousands of dollars) as a function of age, ft by least squares. The dashed curves indicate an estimated 95 % confdence interval. Right: We model the binary event wage>250 using logistic regression, again with a degree-4 polynomial. The ftted posterior probability of wage exceeding $250,000 is shown in blue, along with an estimated 95 % confdence interval.
In Figure 7.1, a pair of dashed curves accompanies the ft; these are (2×) standard error curves. Let’s see how these arise. Suppose we have computed the ft at a particular value of age, x0:
\[ \hat{f}(x\_0) = \hat{\beta}\_0 + \hat{\beta}\_1 x\_0 + \hat{\beta}\_2 x\_0^2 + \hat{\beta}\_3 x\_0^3 + \hat{\beta}\_4 x\_0^4. \tag{7.2} \]
What is the variance of the ft, i.e. Var ˆf(x0)? Least squares returns variance estimates for each of the ftted coefcients βˆj , as well as the covariances between pairs of coefcient estimates. We can use these to compute the estimated variance of ˆf(x0). 1 The estimated pointwise standard error of ˆf(x0) is the square-root of this variance. This computation is repeated at each reference point x0, and we plot the ftted curve, as well as twice the standard error on either side of the ftted curve. We plot twice the standard error because, for normally distributed error terms, this quantity corresponds to an approximate 95 % confdence interval.
It seems like the wages in Figure 7.1 are from two distinct populations: there appears to be a high earners group earning more than $250,000 per annum, as well as a low earners group. We can treat wage as a binary variable by splitting it into these two groups. Logistic regression can then be used to predict this binary response, using polynomial functions of age
1If Cˆ is the 5 × 5 covariance matrix of the βˆj , and if ℓT 0 = (1, x0, x2 0, x3 0, x4 0), then Var[f ˆ(x0)] = ℓT 0 Cˆ ℓ0.
292 7. Moving Beyond Linearity
as predictors. In other words, we ft the model
\[\Pr(y\_i > 250 | x\_i) = \frac{\exp(\beta\_0 + \beta\_1 x\_i + \beta\_2 x\_i^2 + \dots + \beta\_d x\_i^d)}{1 + \exp(\beta\_0 + \beta\_1 x\_i + \beta\_2 x\_i^2 + \dots + \beta\_d x\_i^d)}. \tag{7.3}\]
The result is shown in the right-hand panel of Figure 7.1. The gray marks on the top and bottom of the panel indicate the ages of the high earners and the low earners. The solid blue curve indicates the ftted probabilities of being a high earner, as a function of age. The estimated 95 % confdence interval is shown as well. We see that here the confdence intervals are fairly wide, especially on the right-hand side. Although the sample size for this data set is substantial (n = 3,000), there are only 79 high earners, which results in a high variance in the estimated coefcients and consequently wide confdence intervals.
7.2 Step Functions
Using polynomial functions of the features as predictors in a linear model imposes a global structure on the non-linear function of X. We can instead use step functions in order to avoid imposing such a global structure. Here step we break the range of X function into bins, and ft a diferent constant in each bin. This amounts to converting a continuous variable into an ordered categorical variable. ordered
In greater detail, we create cutpoints c1, c2,…,cK in the range of X, and then construct K + 1 new variables
categorical variable
\[\begin{array}{lcl}C\_0(X) &=& I(X < c\_1), \\ C\_1(X) &=& I(c\_1 \le X < c\_2), \\ C\_2(X) &=& I(c\_2 \le X < c\_3), \\ &\vdots & \\ C\_{K-1}(X) &=& I(c\_{K-1} \le X < c\_K), \\ C\_K(X) &=& I(c\_K \le X), \end{array} \tag{7.4}\]
where I(·) is an indicator function that returns a 1 if the condition is true, indicator function and returns a 0 otherwise. For example, I(cK ≤ X) equals 1 if cK ≤ X, and equals 0 otherwise. These are sometimes called dummy variables. Notice that for any value of X, C0(X) + C1(X) + ··· + CK(X)=1, since X must be in exactly one of the K + 1 intervals. We then use least squares to ft a linear model using C1(X), C2(X),…,CK(X) as predictors2:
\[y\_i = \beta\_0 + \beta\_1 C\_1(x\_i) + \beta\_2 C\_2(x\_i) + \dots + \beta\_K C\_K(x\_i) + \epsilon\_i. \tag{7.5}\]
For a given value of X, at most one of C1, C2,…,CK can be non-zero. Note that when X<c1, all of the predictors in (7.5) are zero, so β0 can
2We exclude C0(X) as a predictor in (7.5) because it is redundant with the intercept. This is similar to the fact that we need only two dummy variables to code a qualitative variable with three levels, provided that the model will contain an intercept. The decision to exclude C0(X) instead of some other Ck(X) in (7.5) is arbitrary. Alternatively, we could include C0(X), C1(X),…,CK(X), and exclude the intercept.
Piecewise Constant
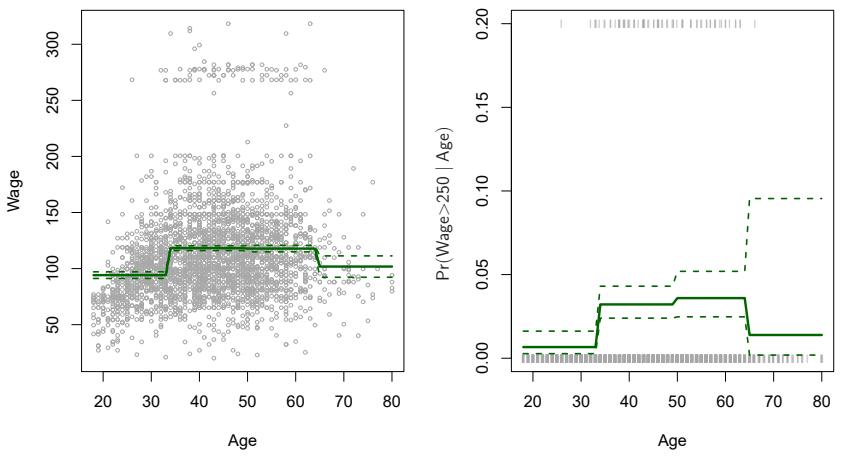
FIGURE 7.2. The Wage data. Left: The solid curve displays the ftted value from a least squares regression of wage (in thousands of dollars) using step functions of age. The dashed curves indicate an estimated 95 % confdence interval. Right: We model the binary event wage>250 using logistic regression, again using step functions of age. The ftted posterior probability of wage exceeding $250,000 is shown, along with an estimated 95 % confdence interval.
be interpreted as the mean value of Y for X<c1. By comparison, (7.5) predicts a response of β0+βj for cj ≤ X<cj+1, so βj represents the average increase in the response for X in cj ≤ X<cj+1 relative to X<c1.
An example of ftting step functions to the Wage data from Figure 7.1 is shown in the left-hand panel of Figure 7.2. We also ft the logistic regression model
\[\Pr(y\_i > 250 | x\_i) = \frac{\exp(\beta\_0 + \beta\_1 C\_1(x\_i) + \dots + \beta\_K C\_K(x\_i))}{1 + \exp(\beta\_0 + \beta\_1 C\_1(x\_i) + \dots + \beta\_K C\_K(x\_i))} \tag{7.6}\]
in order to predict the probability that an individual is a high earner on the basis of age. The right-hand panel of Figure 7.2 displays the ftted posterior probabilities obtained using this approach.
Unfortunately, unless there are natural breakpoints in the predictors, piecewise-constant functions can miss the action. For example, in the lefthand panel of Figure 7.2, the frst bin clearly misses the increasing trend of wage with age. Nevertheless, step function approaches are very popular in biostatistics and epidemiology, among other disciplines. For example, 5-year age groups are often used to defne the bins.
7.3 Basis Functions
Polynomial and piecewise-constant regression models are in fact special cases of a basis function approach. The idea is to have at hand a fam- basis
function
ily of functions or transformations that can be applied to a variable X: b1(X), b2(X),…,bK(X). Instead of ftting a linear model in X, we ft the model
\[y\_i = \beta\_0 + \beta\_1 b\_1(x\_i) + \beta\_2 b\_2(x\_i) + \beta\_3 b\_3(x\_i) + \dots + \beta\_K b\_K(x\_i) + \epsilon\_i. \tag{7.7}\]
Note that the basis functions b1(·), b2(·),…,bK(·) are fxed and known. (In other words, we choose the functions ahead of time.) For polynomial regression, the basis functions are bj (xi) = xj i , and for piecewise constant functions they are bj (xi) = I(cj ≤ xi < cj+1). We can think of (7.7) as a standard linear model with predictors b1(xi), b2(xi),…,bK(xi). Hence, we can use least squares to estimate the unknown regression coefcients in (7.7). Importantly, this means that all of the inference tools for linear models that are discussed in Chapter 3, such as standard errors for the coefcient estimates and F-statistics for the model’s overall signifcance, are available in this setting.
Thus far we have considered the use of polynomial functions and piecewise constant functions for our basis functions; however, many alternatives are possible. For instance, we can use wavelets or Fourier series to construct basis functions. In the next section, we investigate a very common choice for a basis function: regression splines. regression
spline
7.4 Regression Splines
Now we discuss a fexible class of basis functions that extends upon the polynomial regression and piecewise constant regression approaches that we have just seen.
7.4.1 Piecewise Polynomials
Instead of ftting a high-degree polynomial over the entire range of X, piecewise polynomial regression involves ftting separate low-degree polynomials piecewise over diferent regions of X. For example, a piecewise cubic polynomial works by ftting a cubic regression model of the form
polynomial regression
\[y\_i = \beta\_0 + \beta\_1 x\_i + \beta\_2 x\_i^2 + \beta\_3 x\_i^3 + \epsilon\_i,\tag{7.8}\]
where the coefcients β0, β1, β2, and β3 difer in diferent parts of the range
of X. The points where the coefcients change are called knots. knot For example, a piecewise cubic with no knots is just a standard cubic polynomial, as in (7.1) with d = 3. A piecewise cubic polynomial with a single knot at a point c takes the form
\[y\_i = \begin{cases} \beta\_{01} + \beta\_{11}x\_i + \beta\_{21}x\_i^2 + \beta\_{31}x\_i^3 + \epsilon\_i & \text{if } x\_i < c\\ \beta\_{02} + \beta\_{12}x\_i + \beta\_{22}x\_i^2 + \beta\_{32}x\_i^3 + \epsilon\_i & \text{if } x\_i \ge c. \end{cases}\]
In other words, we ft two diferent polynomial functions to the data, one on the subset of the observations with xi < c, and one on the subset of the observations with xi ≥ c. The frst polynomial function has coefcients
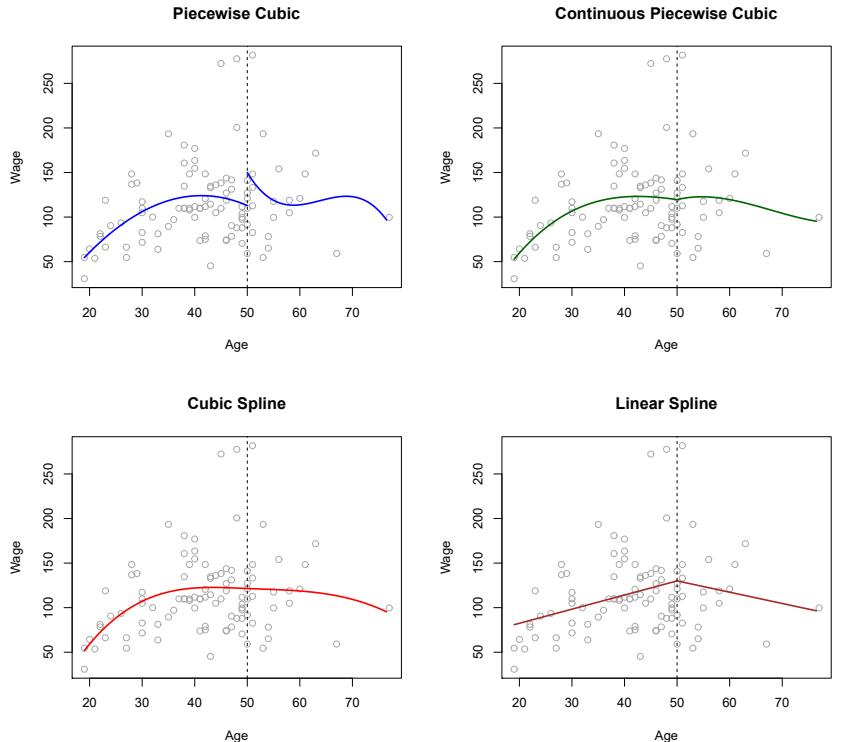
FIGURE 7.3. Various piecewise polynomials are ft to a subset of the Wage data, with a knot at age=50. Top Left: The cubic polynomials are unconstrained. Top Right: The cubic polynomials are constrained to be continuous at age=50. Bottom Left: The cubic polynomials are constrained to be continuous, and to have continuous frst and second derivatives. Bottom Right: A linear spline is shown, which is constrained to be continuous.
β01, β11, β21, and β31, and the second has coefcients β02, β12, β22, and β32. Each of these polynomial functions can be ft using least squares applied to simple functions of the original predictor.
Using more knots leads to a more fexible piecewise polynomial. In general, if we place K diferent knots throughout the range of X, then we will end up ftting K + 1 diferent cubic polynomials. Note that we do not need to use a cubic polynomial. For example, we can instead ft piecewise linear functions. In fact, our piecewise constant functions of Section 7.2 are piecewise polynomials of degree 0!
The top left panel of Figure 7.3 shows a piecewise cubic polynomial ft to a subset of the Wage data, with a single knot at age=50. We immediately see a problem: the function is discontinuous and looks ridiculous! Since each polynomial has four parameters, we are using a total of eight degrees of freedom in ftting this piecewise polynomial model. degrees of
freedom
7.4.2 Constraints and Splines
The top left panel of Figure 7.3 looks wrong because the ftted curve is just too fexible. To remedy this problem, we can ft a piecewise polynomial under the constraint that the ftted curve must be continuous. In other words, there cannot be a jump when age=50. The top right plot in Figure 7.3 shows the resulting ft. This looks better than the top left plot, but the Vshaped join looks unnatural.
In the lower left plot, we have added two additional constraints: now both the frst and second derivatives of the piecewise polynomials are continuous derivative at age=50. In other words, we are requiring that the piecewise polynomial be not only continuous when age=50, but also very smooth. Each constraint that we impose on the piecewise cubic polynomials efectively frees up one degree of freedom, by reducing the complexity of the resulting piecewise polynomial ft. So in the top left plot, we are using eight degrees of freedom, but in the bottom left plot we imposed three constraints (continuity, continuity of the frst derivative, and continuity of the second derivative) and so are left with fve degrees of freedom. The curve in the bottom left plot is called a cubic spline. 3 In general, a cubic spline with K knots uses cubic spline a total of 4 + K degrees of freedom.
In Figure 7.3, the lower right plot is a linear spline, which is continuous linear spline at age=50. The general defnition of a degree-d spline is that it is a piecewise degree-d polynomial, with continuity in derivatives up to degree d − 1 at each knot. Therefore, a linear spline is obtained by ftting a line in each region of the predictor space defned by the knots, requiring continuity at each knot.
In Figure 7.3, there is a single knot at age=50. Of course, we could add more knots, and impose continuity at each.
7.4.3 The Spline Basis Representation
The regression splines that we just saw in the previous section may have seemed somewhat complex: how can we ft a piecewise degree-d polynomial under the constraint that it (and possibly its frst d − 1 derivatives) be continuous? It turns out that we can use the basis model (7.7) to represent a regression spline. A cubic spline with K knots can be modeled as
\[y\_i = \beta\_0 + \beta\_1 b\_1(x\_i) + \beta\_2 b\_2(x\_i) + \dots + \beta\_{K+3} b\_{K+3}(x\_i) + \epsilon\_i,\tag{7.9}\]
for an appropriate choice of basis functions b1, b2,…,bK+3. The model (7.9) can then be ft using least squares.
Just as there were several ways to represent polynomials, there are also many equivalent ways to represent cubic splines using diferent choices of basis functions in (7.9). The most direct way to represent a cubic spline using (7.9) is to start of with a basis for a cubic polynomial—namely, x, x2, and x3—and then add one truncated power basis function per knot. truncated
power basis
3Cubic splines are popular because most human eyes cannot detect the discontinuity at the knots.
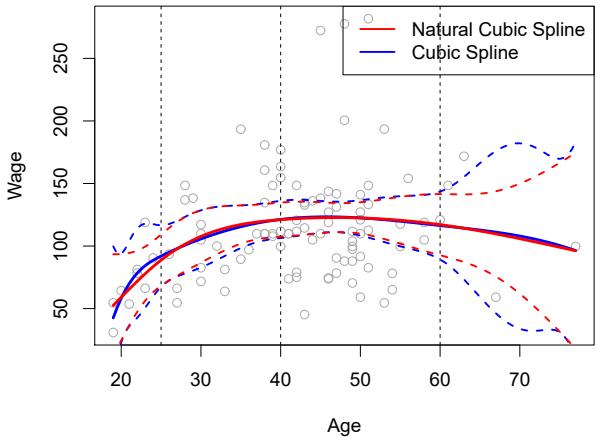
FIGURE 7.4. A cubic spline and a natural cubic spline, with three knots, ft to a subset of the Wage data. The dashed lines denote the knot locations.
A truncated power basis function is defned as
\[h(x,\xi) = (x-\xi)\_+^3 = \begin{cases} \ (x-\xi)^3 & \text{if } x > \xi \\ & 0 \quad \text{otherwise}, \end{cases} \tag{7.10}\]
where ξ is the knot. One can show that adding a term of the form β4h(x, ξ) to the model (7.8) for a cubic polynomial will lead to a discontinuity in only the third derivative at ξ; the function will remain continuous, with continuous frst and second derivatives, at each of the knots.
In other words, in order to ft a cubic spline to a data set with K knots, we perform least squares regression with an intercept and 3 + K predictors, of the form X, X2, X3, h(X, ξ1), h(X, ξ2),…,h(X, ξK), where ξ1,…, ξK are the knots. This amounts to estimating a total of K + 4 regression coefcients; for this reason, ftting a cubic spline with K knots uses K+4 degrees of freedom.
Unfortunately, splines can have high variance at the outer range of the predictors—that is, when X takes on either a very small or very large value. Figure 7.4 shows a ft to the Wage data with three knots. We see that the confdence bands in the boundary region appear fairly wild. A natural spline is a regression spline with additional boundary constraints: the natural spline function is required to be linear at the boundary (in the region where X is smaller than the smallest knot, or larger than the largest knot). This additional constraint means that natural splines generally produce more stable estimates at the boundaries. In Figure 7.4, a natural cubic spline is also displayed as a red line. Note that the corresponding confdence intervals are narrower.
7.4.4 Choosing the Number and Locations of the Knots
When we ft a spline, where should we place the knots? The regression spline is most fexible in regions that contain a lot of knots, because in those regions the polynomial coefcients can change rapidly. Hence, one
Natural Cubic Spline
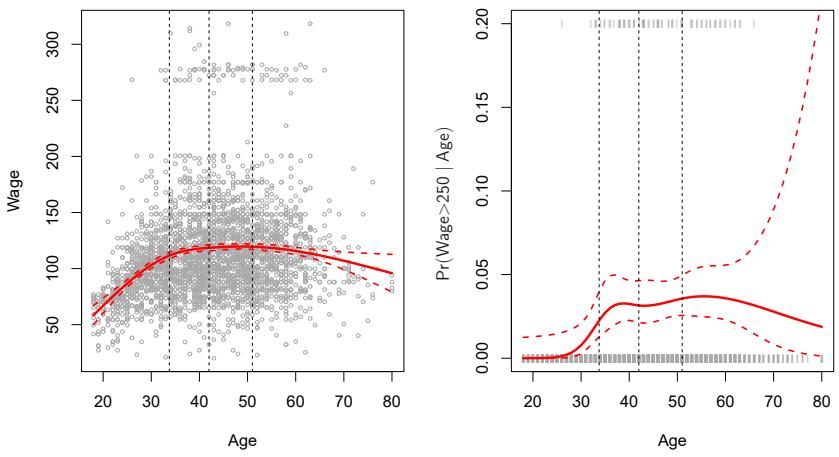
FIGURE 7.5. A natural cubic spline function with four degrees of freedom is ft to the Wage data. Left: A spline is ft to wage (in thousands of dollars) as a function of age. Right: Logistic regression is used to model the binary event wage>250 as a function of age. The ftted posterior probability of wage exceeding $250,000 is shown. The dashed lines denote the knot locations.
option is to place more knots in places where we feel the function might vary most rapidly, and to place fewer knots where it seems more stable. While this option can work well, in practice it is common to place knots in a uniform fashion. One way to do this is to specify the desired degrees of freedom, and then have the software automatically place the corresponding number of knots at uniform quantiles of the data.
Figure 7.5 shows an example on the Wage data. As in Figure 7.4, we have ft a natural cubic spline with three knots, except this time the knot locations were chosen automatically as the 25th, 50th, and 75th percentiles of age. This was specifed by requesting four degrees of freedom. The argument by which four degrees of freedom leads to three interior knots is somewhat technical.4
How many knots should we use, or equivalently how many degrees of freedom should our spline contain? One option is to try out diferent numbers of knots and see which produces the best looking curve. A somewhat more objective approach is to use cross-validation, as discussed in Chapters 5 and 6. With this method, we remove a portion of the data (say 10 %), ft a spline with a certain number of knots to the remaining data, and then use the spline to make predictions for the held-out portion. We repeat this process multiple times until each observation has been left out once, and
4There are actually fve knots, including the two boundary knots. A cubic spline with fve knots has nine degrees of freedom. But natural cubic splines have two additional natural constraints at each boundary to enforce linearity, resulting in 9 − 4=5 degrees of freedom. Since this includes a constant, which is absorbed in the intercept, we count it as four degrees of freedom.
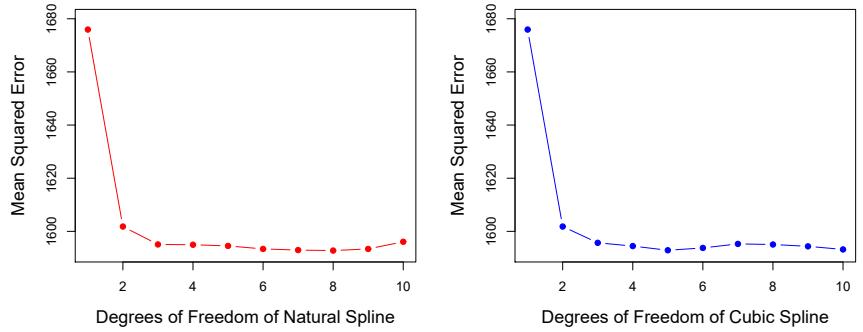
FIGURE 7.6. Ten-fold cross-validated mean squared errors for selecting the degrees of freedom when ftting splines to the Wage data. The response is wage and the predictor age. Left: A natural cubic spline. Right: A cubic spline.
then compute the overall cross-validated RSS. This procedure can be repeated for diferent numbers of knots K. Then the value of K giving the smallest RSS is chosen.
Figure 7.6 shows ten-fold cross-validated mean squared errors for splines with various degrees of freedom ft to the Wage data. The left-hand panel corresponds to a natural cubic spline and the right-hand panel to a cubic spline. The two methods produce almost identical results, with clear evidence that a one-degree ft (a linear regression) is not adequate. Both curves fatten out quickly, and it seems that three degrees of freedom for the natural spline and four degrees of freedom for the cubic spline are quite adequate.
In Section 7.7 we ft additive spline models simultaneously on several variables at a time. This could potentially require the selection of degrees of freedom for each variable. In cases like this we typically adopt a more pragmatic approach and set the degrees of freedom to a fxed number, say four, for all terms.
7.4.5 Comparison to Polynomial Regression
Figure 7.7 compares a natural cubic spline with 15 degrees of freedom to a degree-15 polynomial on the Wage data set. The extra fexibility in the polynomial produces undesirable results at the boundaries, while the natural cubic spline still provides a reasonable ft to the data. Regression splines often give superior results to polynomial regression. This is because unlike polynomials, which must use a high degree (exponent in the highest monomial term, e.g. X15) to produce fexible fts, splines introduce fexibility by increasing the number of knots but keeping the degree fxed. Generally, this approach produces more stable estimates. Splines also allow us to place more knots, and hence fexibility, over regions where the function f seems to be changing rapidly, and fewer knots where f appears more stable.
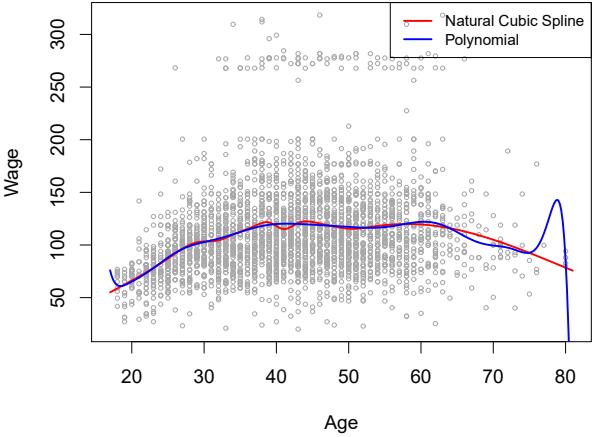
FIGURE 7.7. On the Wage data set, a natural cubic spline with 15 degrees of freedom is compared to a degree-15 polynomial. Polynomials can show wild behavior, especially near the tails.
7.5 Smoothing Splines
In the last section we discussed regression splines, which we create by specifying a set of knots, producing a sequence of basis functions, and then using least squares to estimate the spline coefcients. We now introduce a somewhat diferent approach that also produces a spline.
7.5.1 An Overview of Smoothing Splines
In ftting a smooth curve to a set of data, what we really want to do is fnd some function, say g(x), that fts the observed data well: that is, we want RSS = #n i=1(yi − g(xi))2 to be small. However, there is a problem with this approach. If we don’t put any constraints on g(xi), then we can always make RSS zero simply by choosing g such that it interpolates all of the yi. Such a function would woefully overft the data—it would be far too fexible. What we really want is a function g that makes RSS small, but that is also smooth.
How might we ensure that g is smooth? There are a number of ways to do this. A natural approach is to fnd the function g that minimizes
\[\sum\_{i=1}^{n} (y\_i - g(x\_i))^2 + \lambda \int g''(t)^2 dt\tag{7.11}\]
where λ is a nonnegative tuning parameter. The function g that minimizes
(7.11) is known as a smoothing spline. smoothing What does ( spline 7.11) mean? Equation 7.11 takes the “Loss+Penalty” formulation that we encounter in the context of ridge regression and the lasso in Chapter 6. The term #n i=1(yi − g(xi))2 is a loss function that encour- loss function ages g to ft the data well, and the term λ & g′′(t)2dt is a penalty term that penalizes the variability in g. The notation g′′(t) indicates the second derivative of the function g. The frst derivative g′ (t) measures the slope
of a function at t, and the second derivative corresponds to the amount by which the slope is changing. Hence, broadly speaking, the second derivative of a function is a measure of its roughness: it is large in absolute value if g(t) is very wiggly near t, and it is close to zero otherwise. (The second derivative of a straight line is zero; note that a line is perfectly smooth.) The & notation is an integral, which we can think of as a summation over the range of t. In other words, & g′′(t)2dt is simply a measure of the total change in the function g′ (t), over its entire range. If g is very smooth, then g′ (t) will be close to constant and & g′′(t)2dt will take on a small value. Conversely, if g is jumpy and variable then g′ (t) will vary signifcantly and & g′′(t)2dt will take on a large value. Therefore, in (7.11), λ & g′′(t)2dt encourages g to be smooth. The larger the value of λ, the smoother g will be.
When λ = 0, then the penalty term in (7.11) has no efect, and so the function g will be very jumpy and will exactly interpolate the training observations. When λ → ∞, g will be perfectly smooth—it will just be a straight line that passes as closely as possible to the training points. In fact, in this case, g will be the linear least squares line, since the loss function in (7.11) amounts to minimizing the residual sum of squares. For an intermediate value of λ, g will approximate the training observations but will be somewhat smooth. We see that λ controls the bias-variance trade-of of the smoothing spline.
The function g(x) that minimizes (7.11) can be shown to have some special properties: it is a piecewise cubic polynomial with knots at the unique values of x1,…,xn, and continuous frst and second derivatives at each knot. Furthermore, it is linear in the region outside of the extreme knots. In other words, the function g(x) that minimizes (7.11) is a natural cubic spline with knots at x1,…,xn! However, it is not the same natural cubic spline that one would get if one applied the basis function approach described in Section 7.4.3 with knots at x1,…,xn—rather, it is a shrunken version of such a natural cubic spline, where the value of the tuning parameter λ in (7.11) controls the level of shrinkage.
7.5.2 Choosing the Smoothing Parameter λ
We have seen that a smoothing spline is simply a natural cubic spline with knots at every unique value of xi. It might seem that a smoothing spline will have far too many degrees of freedom, since a knot at each data point allows a great deal of fexibility. But the tuning parameter λ controls the roughness of the smoothing spline, and hence the efective degrees of freedom. It is possible to show that as λ increases from 0 to ∞, the efective efective degrees of freedom, which we write dfλ, decrease from n to 2.
degrees of freedom
In the context of smoothing splines, why do we discuss efective degrees of freedom instead of degrees of freedom? Usually degrees of freedom refer to the number of free parameters, such as the number of coefcients ft in a polynomial or cubic spline. Although a smoothing spline has n parameters and hence n nominal degrees of freedom, these n parameters are heavily constrained or shrunk down. Hence dfλ is a measure of the fexibility of the smoothing spline—the higher it is, the more fexible (and the lower-bias but higher-variance) the smoothing spline. The defnition of efective degrees of freedom is somewhat technical. We can write
\[ \hat{\mathbf{g}}\_{\lambda} = \mathbf{S}\_{\lambda} \mathbf{y},\tag{7.12} \]
where gˆλ is the solution to (7.11) for a particular choice of λ—that is, it is an n-vector containing the ftted values of the smoothing spline at the training points x1,…,xn. Equation 7.12 indicates that the vector of ftted values when applying a smoothing spline to the data can be written as a n × n matrix Sλ (for which there is a formula) times the response vector y. Then the efective degrees of freedom is defned to be
\[df\_{\lambda} = \sum\_{i=1}^{n} \{ \mathbf{S}\_{\lambda} \}\_{ii},\tag{7.13}\]
the sum of the diagonal elements of the matrix Sλ.
In ftting a smoothing spline, we do not need to select the number or location of the knots—there will be a knot at each training observation, x1,…,xn. Instead, we have another problem: we need to choose the value of λ. It should come as no surprise that one possible solution to this problem is cross-validation. In other words, we can fnd the value of λ that makes the cross-validated RSS as small as possible. It turns out that the leaveone-out cross-validation error (LOOCV) can be computed very efciently for smoothing splines, with essentially the same cost as computing a single ft, using the following formula:
\[\text{RSS}\_{cv}(\lambda) = \sum\_{i=1}^{n} (y\_i - \hat{g}\_{\lambda}^{(-i)}(x\_i))^2 = \sum\_{i=1}^{n} \left[ \frac{y\_i - \hat{g}\_{\lambda}(x\_i)}{1 - \{\mathbf{S}\_{\lambda}\}\_{ii}} \right]^2 \cdot \mathbf{1}\]
The notation gˆ (−i) λ (xi) indicates the ftted value for this smoothing spline evaluated at xi, where the ft uses all of the training observations except for the ith observation (xi, yi). In contrast, gˆλ(xi) indicates the smoothing spline function ft to all of the training observations and evaluated at xi. This remarkable formula says that we can compute each of these leaveone-out fts using only gˆλ, the original ft to all of the data We have a very similar formula (5.2) on page 205 in Chapter 5 for least squares linear regression. Using (5.2), we can very quickly perform LOOCV for the regression splines discussed earlier in this chapter, as well as for least squares regression using arbitrary basis functions.
We have a very similar formula (5.2) on page 205 in Chapter 5 for least squares linear regression. Using (5.2), we can very quickly perform LOOCV for the regression splines discussed earlier in this chapter, as well as for least squares regression using arbitrary basis functions.
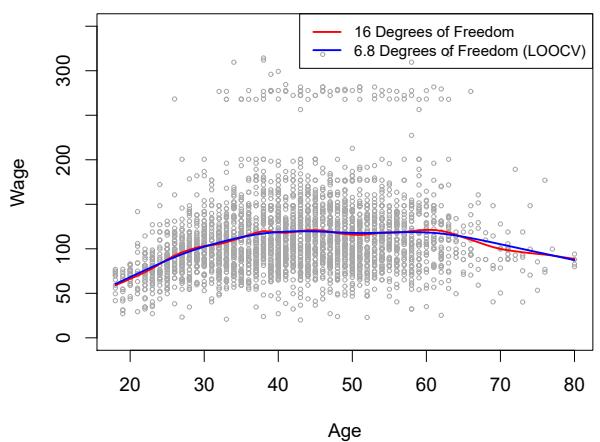
Figure 7.8 shows the results from ftting a smoothing spline to the Wage data. The red curve indicates the ft obtained from pre-specifying that we would like a smoothing spline with 16 efective degrees of freedom. The blue curve is the smoothing spline obtained when λ is chosen using LOOCV; in this case, the value of λ chosen results in 6.8 efective degrees of freedom (computed using (7.13)). For this data, there is little discernible diference between the two smoothing splines, beyond the fact that the one with 16 degrees of freedom seems slightly wigglier. Since there is little diference between the two fts, the smoothing spline ft with 6.8 degrees of freedom
5The exact formulas for computing gˆ(xi) and Sλ are very technical; however, efcient algorithms are available for computing these quantities.
Smoothing Spline
FIGURE 7.8. Smoothing spline fts to the Wage data. The red curve results from specifying 16 efective degrees of freedom. For the blue curve, λ was found automatically by leave-one-out cross-validation, which resulted in 6.8 efective degrees of freedom.
is preferable, since in general simpler models are better unless the data provides evidence in support of a more complex model.
7.6 Local Regression
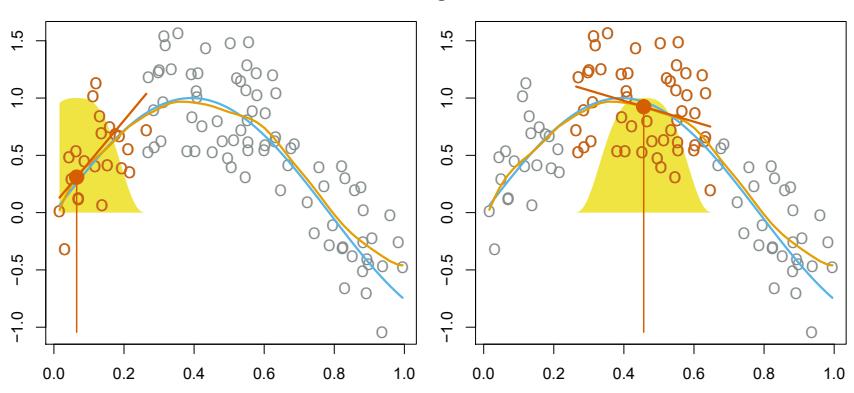
Local regression is a diferent approach for ftting fexible non-linear func- local regression tions, which involves computing the ft at a target point x0 using only the nearby training observations. Figure 7.9 illustrates the idea on some simulated data, with one target point near 0.4, and another near the boundary at 0.05. In this fgure the blue line represents the function f(x) from which the data were generated, and the light orange line corresponds to the local regression estimate ˆf(x). Local regression is described in Algorithm 7.1.
Note that in Step 3 of Algorithm 7.1, the weights Ki0 will difer for each value of x0. In other words, in order to obtain the local regression ft at a new point, we need to ft a new weighted least squares regression model by minimizing (7.14) for a new set of weights. Local regression is sometimes referred to as a memory-based procedure, because like nearest-neighbors, we need all the training data each time we wish to compute a prediction. We will avoid getting into the technical details of local regression here—there are books written on the topic.
In order to perform local regression, there are a number of choices to be made, such as how to defne the weighting function K, and whether to ft a linear, constant, or quadratic regression in Step 3. (Equation 7.14 corresponds to a linear regression.) While all of these choices make some diference, the most important choice is the span s, which is the proportion of points used to compute the local regression at x0, as defned in Step 1 above. The span plays a role like that of the tuning parameter λ in smooth-
Local Regression
FIGURE 7.9. Local regression illustrated on some simulated data, where the blue curve represents f(x) from which the data were generated, and the light orange curve corresponds to the local regression estimate ˆf(x). The orange colored points are local to the target point x0, represented by the orange vertical line. The yellow bell-shape superimposed on the plot indicates weights assigned to each point, decreasing to zero with distance from the target point. The ft ˆf(x0) at x0 is obtained by ftting a weighted linear regression (orange line segment), and using the ftted value at x0 (orange solid dot) as the estimate ˆf(x0).
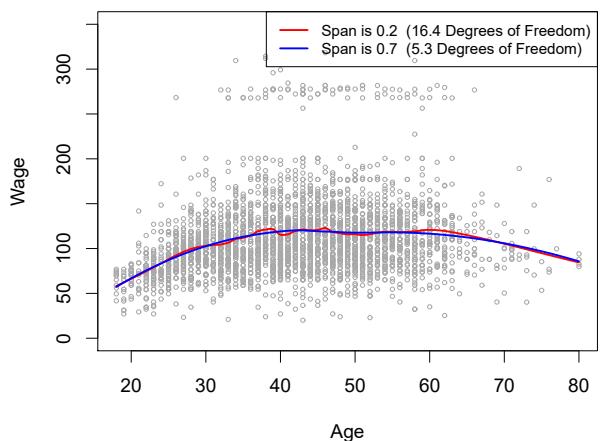
ing splines: it controls the fexibility of the non-linear ft. The smaller the value of s, the more local and wiggly will be our ft; alternatively, a very large value of s will lead to a global ft to the data using all of the training observations. We can again use cross-validation to choose s, or we can specify it directly. Figure 7.10 displays local linear regression fts on the Wage data, using two values of s: 0.7 and 0.2. As expected, the ft obtained using s = 0.7 is smoother than that obtained using s = 0.2.
The idea of local regression can be generalized in many diferent ways. In a setting with multiple features X1, X2,…,Xp, one very useful generalization involves ftting a multiple linear regression model that is global in some variables, but local in another, such as time. Such varying coefcient models are a useful way of adapting a model to the most recently gathered varying data. Local regression also generalizes very naturally when we want to ft models that are local in a pair of variables X1 and X2, rather than one. We can simply use two-dimensional neighborhoods, and ft bivariate linear regression models using the observations that are near each target point in two-dimensional space. Theoretically the same approach can be implemented in higher dimensions, using linear regressions ft to p-dimensional neighborhoods. However, local regression can perform poorly if p is much larger than about 3 or 4 because there will generally be very few training observations close to x0. Nearest-neighbors regression, discussed in Chapter 3, sufers from a similar problem in high dimensions.
coefcient model
Algorithm 7.1 Local Regression At X = x0
- Gather the fraction s = k/n of training points whose xi are closest to x0.
- Assign a weight Ki0 = K(xi, x0) to each point in this neighborhood, so that the point furthest from x0 has weight zero, and the closest has the highest weight. All but these k nearest neighbors get weight zero.
- Fit a weighted least squares regression of the yi on the xi using the aforementioned weights, by fnding βˆ0 and βˆ1 that minimize
\[\sum\_{i=1}^{n} K\_{i0} (y\_i - \beta\_0 - \beta\_1 x\_i)^2. \tag{7.14}\]
- The ftted value at x0 is given by ˆf(x0) = βˆ0 + βˆ1x0.
Local Linear Regression
FIGURE 7.10. Local linear fts to the Wage data. The span specifes the fraction of the data used to compute the ft at each target point.
7.7 Generalized Additive Models
In Sections 7.1–7.6, we present a number of approaches for fexibly predicting a response Y on the basis of a single predictor X. These approaches can be seen as extensions of simple linear regression. Here we explore the problem of fexibly predicting Y on the basis of several predictors, X1,…,Xp. This amounts to an extension of multiple linear regression.
Generalized additive models (GAMs) provide a general framework for generalized extending a standard linear model by allowing non-linear functions of each of the variables, while maintaining additivity. Just like linear models, GAMs can be applied with both quantitative and qualitative responses. We frst additivity
additive model
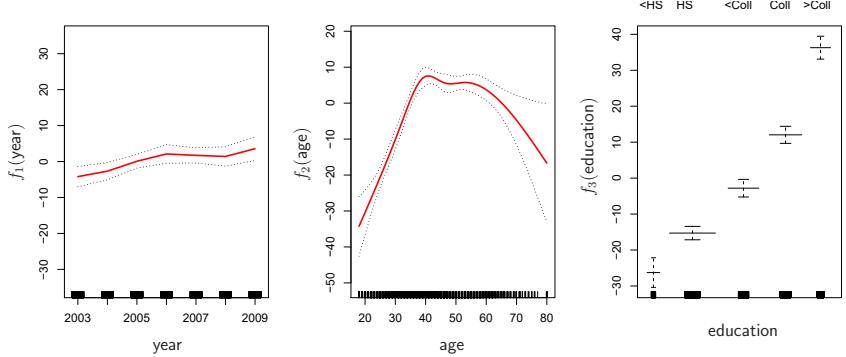
FIGURE 7.11. For the Wage data, plots of the relationship between each feature and the response, wage, in the ftted model (7.16). Each plot displays the ftted function and pointwise standard errors. The frst two functions are natural splines in year and age, with four and fve degrees of freedom, respectively. The third function is a step function, ft to the qualitative variable education.
examine GAMs for a quantitative response in Section 7.7.1, and then for a qualitative response in Section 7.7.2.
7.7.1 GAMs for Regression Problems
A natural way to extend the multiple linear regression model
\[y\_i = \beta\_0 + \beta\_1 x\_{i1} + \beta\_2 x\_{i2} + \dots + \beta\_p x\_{ip} + \epsilon\_i\]
in order to allow for non-linear relationships between each feature and the response is to replace each linear component βjxij with a (smooth) nonlinear function fj (xij ). We would then write the model as
\[\begin{aligned} y\_i &= \beta\_0 + \sum\_{j=1}^p f\_j(x\_{ij}) + \epsilon\_i \\ &= \beta\_0 + f\_1(x\_{i1}) + f\_2(x\_{i2}) + \dots + f\_p(x\_{ip}) + \epsilon\_i. \end{aligned} \tag{7.15}\]
This is an example of a GAM. It is called an additive model because we calculate a separate fj for each Xj , and then add together all of their contributions.
In Sections 7.1–7.6, we discuss many methods for ftting functions to a single variable. The beauty of GAMs is that we can use these methods as building blocks for ftting an additive model. In fact, for most of the methods that we have seen so far in this chapter, this can be done fairly trivially. Take, for example, natural splines, and consider the task of ftting the model
\[\text{wage} = \beta\_0 + f\_1(\text{year}) + f\_2(\text{age}) + f\_3(\text{education}) + \epsilon \tag{7.16}\]
on the Wage data. Here year and age are quantitative variables, while the variable education is qualitative with fve levels: <HS, HS, <Coll, Coll, >Coll, referring to the amount of high school or college education that an individual has completed. We ft the frst two functions using natural splines. We
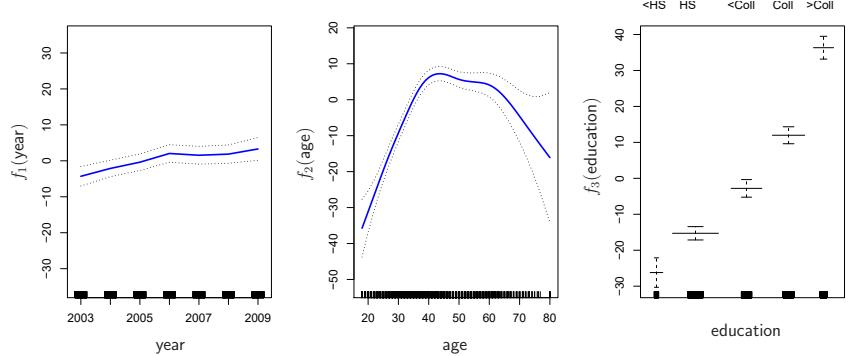
FIGURE 7.12. Details are as in Figure 7.11, but now f1 and f2 are smoothing splines with four and fve degrees of freedom, respectively.
ft the third function using a separate constant for each level, via the usual dummy variable approach of Section 3.3.1.
Figure 7.11 shows the results of ftting the model (7.16) using least squares. This is easy to do, since as discussed in Section 7.4, natural splines can be constructed using an appropriately chosen set of basis functions. Hence the entire model is just a big regression onto spline basis variables and dummy variables, all packed into one big regression matrix.
Figure 7.11 can be easily interpreted. The left-hand panel indicates that holding age and education fxed, wage tends to increase slightly with year; this may be due to infation. The center panel indicates that holding education and year fxed, wage tends to be highest for intermediate values of age, and lowest for the very young and very old. The right-hand panel indicates that holding year and age fxed, wage tends to increase with education: the more educated a person is, the higher their salary, on average. All of these fndings are intuitive.
Figure 7.12 shows a similar triple of plots, but this time f1 and f2 are smoothing splines with four and fve degrees of freedom, respectively. Fitting a GAM with a smoothing spline is not quite as simple as ftting a GAM with a natural spline, since in the case of smoothing splines, least squares cannot be used. However, standard software such as the Python package pygam can be used to ft GAMs using smoothing splines, via an approach pygam known as backftting. This method fts a model involving multiple predic- backftting tors by repeatedly updating the ft for each predictor in turn, holding the others fxed. The beauty of this approach is that each time we update a function, we simply apply the ftting method for that variable to a partial residual. 6
The ftted functions in Figures 7.11 and 7.12 look rather similar. In most situations, the diferences in the GAMs obtained using smoothing splines versus natural splines are small.
6A partial residual for X3, for example, has the form ri = yi −f1(xi1)−f2(xi2). If we know f1 and f2, then we can ft f3 by treating this residual as a response in a non-linear regression on X3.
We do not have to use splines as the building blocks for GAMs: we can just as well use local regression, polynomial regression, or any combination of the approaches seen earlier in this chapter in order to create a GAM. GAMs are investigated in further detail in the lab at the end of this chapter.
Pros and Cons of GAMs
Before we move on, let us summarize the advantages and limitations of a GAM.
- ▲ GAMs allow us to ft a non-linear fj to each Xj , so that we can automatically model non-linear relationships that standard linear regression will miss. This means that we do not need to manually try out many diferent transformations on each variable individually.
- ▲ The non-linear fts can potentially make more accurate predictions for the response Y .
- ▲ Because the model is additive, we can examine the efect of each Xj on Y individually while holding all of the other variables fxed.
- ▲ The smoothness of the function fj for the variable Xj can be summarized via degrees of freedom.
- ◆ The main limitation of GAMs is that the model is restricted to be additive. With many variables, important interactions can be missed. However, as with linear regression, we can manually add interaction terms to the GAM model by including additional predictors of the form Xj × Xk. In addition we can add low-dimensional interaction functions of the form fjk(Xj , Xk) into the model; such terms can be ft using two-dimensional smoothers such as local regression, or two-dimensional splines (not covered here).
For fully general models, we have to look for even more fexible approaches such as random forests and boosting, described in Chapter 8. GAMs provide a useful compromise between linear and fully nonparametric models.
7.7.2 GAMs for Classifcation Problems
GAMs can also be used in situations where Y is qualitative. For simplicity, here we assume Y takes on values 0 or 1, and let p(X) = Pr(Y = 1|X) be the conditional probability (given the predictors) that the response equals one. Recall the logistic regression model (4.6):
\[\log\left(\frac{p(X)}{1 - p(X)}\right) = \beta\_0 + \beta\_1 X\_1 + \beta\_2 X\_2 + \dots + \beta\_p X\_p. \tag{7.17}\]
The left-hand side is the log of the odds of P(Y = 1|X) versus P(Y = 0|X), which (7.17) represents as a linear function of the predictors. A natural way to extend (7.17) to allow for non-linear relationships is to use the model
\[\log\left(\frac{p(X)}{1 - p(X)}\right) = \beta\_0 + f\_1(X\_1) + f\_2(X\_2) + \dots + f\_p(X\_p). \tag{7.18}\]
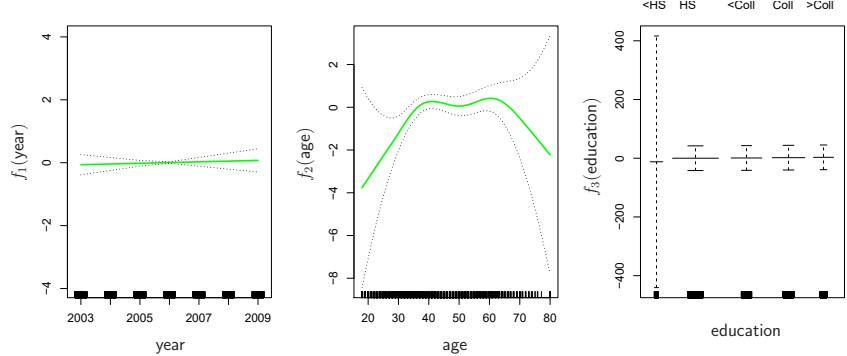
FIGURE 7.13. For the Wage data, the logistic regression GAM given in (7.19) is ft to the binary response I(wage>250). Each plot displays the ftted function and pointwise standard errors. The frst function is linear in year, the second function a smoothing spline with fve degrees of freedom in age, and the third a step function for education. There are very wide standard errors for the frst level <HS of education.
Equation 7.18 is a logistic regression GAM. It has all the same pros and cons as discussed in the previous section for quantitative responses.
We ft a GAM to the Wage data in order to predict the probability that an individual’s income exceeds $250,000 per year. The GAM that we ft takes the form
\[\log\left(\frac{p(X)}{1-p(X)}\right) = \beta\_0 + \beta\_1 \times \text{year} + f\_2(\text{age}) + f\_3(\text{education}), \quad (7.19)\]
where
\[p(X) = \Pr(\text{wage} > 250 | \text{year}, \text{age}, \text{education}).\]
Once again f2 is ft using a smoothing spline with fve degrees of freedom, and f3 is ft as a step function, by creating dummy variables for each of the levels of education. The resulting ft is shown in Figure 7.13. The last panel looks suspicious, with very wide confdence intervals for level <HS. In fact, no response values equal one for that category: no individuals with less than a high school education make more than $250,000 per year. Hence we reft the GAM, excluding the individuals with less than a high school education. The resulting model is shown in Figure 7.14. As in Figures 7.11 and 7.12, all three panels have similar vertical scales. This allows us to visually assess the relative contributions of each of the variables. We observe that age and education have a much larger efect than year on the probability of being a high earner.
7.8 Lab: Non-Linear Modeling
In this lab, we demonstrate some of the nonlinear models discussed in this chapter. We use the Wage data as a running example, and show that many of the complex non-linear ftting procedures discussed can easily be implemented in Python.
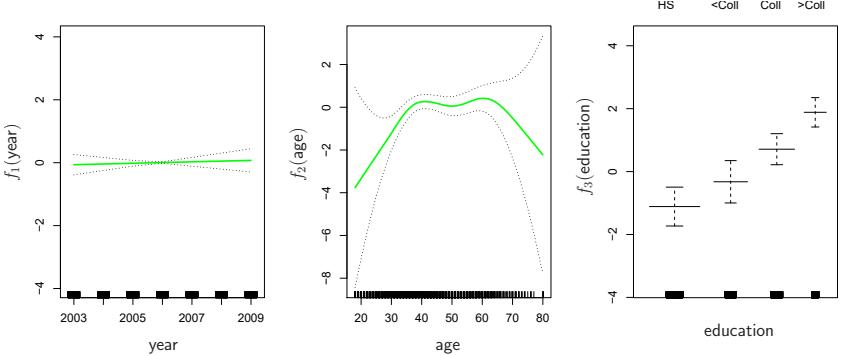
FIGURE 7.14. The same model is ft as in Figure 7.13, this time excluding the observations for which education is <HS. Now we see that increased education tends to be associated with higher salaries.
As usual, we start with some of our standard imports.
In [1]: import numpy as np, pandas as pd
from matplotlib.pyplot import subplots
import statsmodels.api as sm
from ISLP import load_data
from ISLP.models import (summarize,
poly,
ModelSpec as MS)
from statsmodels.stats.anova import anova_lmWe again collect the new imports needed for this lab. Many of these are developed specifcally for the ISLP package.
In [2]: from pygam import (s as s_gam,
l as l_gam,
f as f_gam,
LinearGAM,
LogisticGAM)
from ISLP.transforms import (BSpline,
NaturalSpline)
from ISLP.models import bs, ns
from ISLP.pygam import (approx_lam,
degrees_of_freedom,
plot as plot_gam,
anova as anova_gam)7.8.1 Polynomial Regression and Step Functions
We start by demonstrating how Figure 7.1 can be reproduced. Let’s begin by loading the data.
In [3]: Wage = load_data(‘Wage’) y = Wage[‘wage’] age = Wage[‘age’]
Throughout most of this lab, our response is Wage[‘wage’], which we have stored as y above. As in Section 3.6.6, we will use the poly() function to create a model matrix that will ft a 4th degree polynomial in age.
In [4]: poly_age = MS([poly('age', degree=4)]).fit(Wage)
M = sm.OLS(y, poly_age.transform(Wage)).fit()
summarize(M)Out[4]: coef std err t P>|t|
intercept 111.7036 0.729 153.283 0.000
poly(age, degree=4)[0] 447.0679 39.915 11.201 0.000
poly(age, degree=4)[1] -478.3158 39.915 -11.983 0.000
poly(age, degree=4)[2] 125.5217 39.915 3.145 0.002
poly(age, degree=4)[3] -77.9112 39.915 -1.952 0.051This polynomial is constructed using the function poly(), which creates a special transformer Poly() (using sklearn terminology for feature transformer transformations such as PCA() seen in Section 6.5.3) which allows for easy evaluation of the polynomial at new data points. Here poly() is referred to as a helper function, and sets up the transformation; Poly() is the ac- helper tual workhorse that computes the transformation. See also the discussion of transformations on page 118.
In the code above, the frst line executes the fit() method using the dataframe Wage. This recomputes and stores as attributes any parameters needed by Poly() on the training data, and these will be used on all subsequent evaluations of the transform() method. For example, it is used on the second line, as well as in the plotting function developed below.
We now create a grid of values for age at which we want predictions.
In [5]: age_grid = np.linspace(age.min(),
age.max(),
100)
age_df = pd.DataFrame({'age': age_grid})Finally, we wish to plot the data and add the ft from the fourth-degree polynomial. As we will make several similar plots below, we frst write a function to create all the ingredients and produce the plot. Our function takes in a model specifcation (here a basis specifed by a transform), as well as a grid of age values. The function produces a ftted curve as well as 95% confdence bands. By using an argument for basis we can produce and plot the results with several diferent transforms, such as the splines we will see shortly.
In [6]: def plot_wage_fit(age_df,basis,
title):
X = basis.transform(Wage)
Xnew = basis.transform(age_df)
M = sm.OLS(y, X).fit()
preds = M.get_prediction(Xnew)
bands = preds.conf_int(alpha=0.05)
fig, ax = subplots(figsize=(8,8))
ax.scatter(age,
y,facecolor='gray',
alpha=0.5)
for val, ls in zip([preds.predicted_mean ,
bands[:,0],
bands[:,1]],
['b','r--','r--']):
ax.plot(age_df.values, val, ls, linewidth=3)
ax.set_title(title, fontsize=20)
ax.set_xlabel('Age', fontsize=20)
ax.set_ylabel('Wage', fontsize=20);
return axWe include an argument alpha to ax.scatter() to add some transparency to the points. This provides a visual indication of density. Notice the use of the zip() function in the for loop above (see Section 2.3.8). We have three lines to plot, each with diferent colors and line types. Here zip() conveniently bundles these together as iterators in the loop.7
iterator We now plot the ft of the fourth-degree polynomial using this function.
In [7]: plot_wage_fit(age_df,poly_age,
'Degree-4 Polynomial');With polynomial regression we must decide on the degree of the polynomial to use. Sometimes we just wing it, and decide to use second or third degree polynomials, simply to obtain a nonlinear ft. But we can make such a decision in a more systematic way. One way to do this is through hypothesis tests, which we demonstrate here. We now ft a series of models ranging from linear (degree-one) to degree-fve polynomials, and look to determine the simplest model that is sufcient to explain the relationship between wage and age. We use the anova_lm() function, which performs a series of ANOVA tests. An analysis of variance or ANOVA tests the null hypothesis analysis of variance that a model M1 is sufcient to explain the data against the alternative hypothesis that a more complex model M2 is required. The determination is based on an F-test. To perform the test, the models M1 and M2 must be nested: the space spanned by the predictors in M1 must be a subspace of the space spanned by the predictors in M2. In this case, we ft fve different polynomial models and sequentially compare the simpler model to the more complex model.
In [8]: models = [MS([poly('age', degree=d)])
for d in range(1, 6)]
Xs = [model.fit_transform(Wage) for model in models]
anova_lm(*[sm.OLS(y, X_).fit()
for X_ in Xs])| Out[8]: | df_resid | ssr | df_diff | ss_diff | F | Pr(>F) | |
|---|---|---|---|---|---|---|---|
| 0 | 2998.0 | 5.022e+06 | 0.0 | NaN | NaN | NaN | |
| 1 | 2997.0 | 4.793e+06 | 1.0 | 228786.010 | 143.593 | 2.364e-32 | |
| 2 | 2996.0 | 4.778e+06 | 1.0 | 15755.694 | 9.889 | 1.679e-03 | |
| 3 | 2995.0 | 4.772e+06 | 1.0 | 6070.152 | 3.810 | 5.105e-02 |
7In Python speak, an “iterator” is an object with a fnite number of values, that can be iterated on, as in a loop.
4 2994.0 4.770e+06 1.0 1282.563 0.805 3.697e-01
Notice the * in the anova_lm() line above. This function takes a variable number of non-keyword arguments, in this case ftted models. When these models are provided as a list (as is done here), it must be prefxed by *.
The p-value comparing the linear models[0] to the quadratic models[1] is essentially zero, indicating that a linear ft is not sufcient.8 Similarly the p-value comparing the quadratic models[1] to the cubic models[2] is very low (0.0017), so the quadratic ft is also insufcient. The p-value comparing the cubic and degree-four polynomials, models[2] and models[3], is approximately 5%, while the degree-fve polynomial models[4] seems unnecessary because its p-value is 0.37. Hence, either a cubic or a quartic polynomial appear to provide a reasonable ft to the data, but lower- or higher-order models are not justifed.
In this case, instead of using the anova() function, we could have obtained these p-values more succinctly by exploiting the fact that poly() creates orthogonal polynomials.
In [9]: summarize(M)Out[9]: coef std err t P>|t|
intercept 111.7036 0.729 153.283 0.000
poly(age, degree=4)[0] 447.0679 39.915 11.201 0.000
poly(age, degree=4)[1] -478.3158 39.915 -11.983 0.000
poly(age, degree=4)[2] 125.5217 39.915 3.145 0.002
poly(age, degree=4)[3] -77.9112 39.915 -1.952 0.051Notice that the p-values are the same, and in fact the square of the t-statistics are equal to the F-statistics from the anova_lm() function; for example:
In [10]: (-11.983)**2
Out[10]: 143.59228
However, the ANOVA method works whether or not we used orthogonal polynomials, provided the models are nested. For example, we can use anova_lm() to compare the following three models, which all have a linear term in education and a polynomial in age of diferent degrees:
In [11]: models = [MS(['education', poly('age', degree=d)])
for d in range(1, 4)]
XEs = [model.fit_transform(Wage)
for model in models]
anova_lm(*[sm.OLS(y, X_).fit() for X_ in XEs])| Out[11]: | df_resid | ssr | df_diff | ss_diff | F | Pr(>F) | |
|---|---|---|---|---|---|---|---|
| 0 | 2997.0 | 3.902e+06 | 0.0 | NaN | NaN | NaN | |
| 1 | 2996.0 | 3.759e+06 | 1.0 | 142862.701 | 113.992 | 3.838e-26 | |
| 2 | 2995.0 | 3.754e+06 | 1.0 | 5926.207 | 4.729 | 2.974e-02 |
8Indexing starting at zero is confusing for the polynomial degree example, since models[1] is quadratic rather than linear!
As an alternative to using hypothesis tests and ANOVA, we could choose the polynomial degree using cross-validation, as discussed in Chapter 5.
Next we consider the task of predicting whether an individual earns more than $250,000 per year. We proceed much as before, except that frst we create the appropriate response vector, and then apply the glm() function using the binomial family in order to ft a polynomial logistic regression model.
In [12]: X = poly_age.transform(Wage)
high_earn = Wage['high_earn'] = y > 250 # shorthand
glm = sm.GLM(y > 250,
X,
family=sm.families.Binomial())
B = glm.fit()
summarize(B)Out[12]: coef std err z P>|z| intercept -4.3012 0.345 -12.457 0.000 poly(age, degree=4)[0] 71.9642 26.133 2.754 0.006 poly(age, degree=4)[1] -85.7729 35.929 -2.387 0.017 poly(age, degree=4)[2] 34.1626 19.697 1.734 0.083 poly(age, degree=4)[3] -47.4008 24.105 -1.966 0.049
Once again, we make predictions using the get_prediction() method.
In [13]: newX = poly_age.transform(age_df)
preds = B.get_prediction(newX)
bands = preds.conf_int(alpha=0.05)We now plot the estimated relationship.
In [14]: fig, ax = subplots(figsize=(8,8))
rng = np.random.default_rng(0)
ax.scatter(age +
0.2 * rng.uniform(size=y.shape[0]),
np.where(high_earn, 0.198, 0.002),
fc='gray',
marker='|')
for val, ls in zip([preds.predicted_mean ,
bands[:,0],
bands[:,1]],
['b','r--','r--']):
ax.plot(age_df.values, val, ls, linewidth=3)
ax.set_title('Degree-4 Polynomial', fontsize=20)
ax.set_xlabel('Age', fontsize=20)
ax.set_ylim([0,0.2])
ax.set_ylabel('P(Wage > 250)', fontsize=20);We have drawn the age values corresponding to the observations with wage values above 250 as gray marks on the top of the plot, and those with wage values below 250 are shown as gray marks on the bottom of the plot. We added a small amount of noise to jitter the age values a bit so that observations with the same age value do not cover each other up. This type
of plot is often called a rug plot. rug plot In order to ft a step function, as discussed in Section 7.2, we frst use the pd.qcut() function to discretize age based on quantiles. Then we use pd.qcut()
pd.get_dummies() to create the columns of the model matrix for this catedummies() gorical variable. Note that this function will include all columns for a given categorical, rather than the usual approach which drops one of the levels.
pd.get_
| In [15]: | cut_age = pd.qcut(age, 4) summarize(sm.OLS(y, pd.get_dummies(cut_age)).fit()) |
|||||||
|---|---|---|---|---|---|---|---|---|
| Out[15]: | coef | std err |
t | P> t | ||||
| (17.999, 33.75] |
94.1584 | 1.478 | 63.692 | 0.0 | ||||
| (33.75, 42.0] |
116.6608 | 1.470 | 79.385 | 0.0 | ||||
| (42.0, 51.0] |
119.1887 | 1.416 | 84.147 | 0.0 | ||||
| (51.0, 80.0] |
116.5717 | 1.559 | 74.751 | 0.0 |
Here pd.qcut() automatically picked the cutpoints based on the quantiles 25%, 50% and 75%, which results in four regions. We could also have specifed our own quantiles directly instead of the argument 4. For cuts not based on quantiles we would use the pd.cut() function. The function pd.cut() pd.qcut() (and pd.cut()) returns an ordered categorical variable. The regression model then creates a set of dummy variables for use in the regression. Since age is the only variable in the model, the value $94,158.40 is the average salary for those under 33.75 years of age, and the other coefcients are the average salary for those in the other age groups. We can produce predictions and plots just as we did in the case of the polynomial ft.
7.8.2 Splines
In order to ft regression splines, we use transforms from the ISLP package. The actual spline evaluation functions are in the scipy.interpolate package; we have simply wrapped them as transforms similar to Poly() and PCA().
In Section 7.4, we saw that regression splines can be ft by constructing an appropriate matrix of basis functions. The BSpline() function generates BSpline() the entire matrix of basis functions for splines with the specifed set of knots. By default, the B-splines produced are cubic. To change the degree, use the argument degree.
In [16]: bs_ = BSpline(internal_knots=[25,40,60], intercept=True).fit(age)
bs_age = bs_.transform(age)
bs_age.shapeOut[16]: (3000, 7)
This results in a seven-column matrix, which is what is expected for a cubicspline basis with 3 interior knots. We can form this same matrix using the bs() object, which facilitates adding this to a model-matrix builder (as in poly() versus its workhorse Poly()) described in Section 7.8.1.
We now ft a cubic spline model to the Wage data.
In [17]: bs_age = MS([bs('age', internal_knots=[25,40,60])])
Xbs = bs_age.fit_transform(Wage)
M = sm.OLS(y, Xbs).fit()
summarize(M)316 7. Moving Beyond Linearity
Out[17]: coef std err ...
intercept 60.494 9.460 ...
bs(age, internal_knots=[25, 40, 60])[0] 3.980 12.538 ...
bs(age, internal_knots=[25, 40, 60])[1] 44.631 9.626 ...
bs(age, internal_knots=[25, 40, 60])[2] 62.839 10.755 ...
bs(age, internal_knots=[25, 40, 60])[3] 55.991 10.706 ...
bs(age, internal_knots=[25, 40, 60])[4] 50.688 14.402 ...
bs(age, internal_knots=[25, 40, 60])[5] 16.606 19.126 ...The column names are a little cumbersome, and have caused us to truncate the printed summary. They can be set on construction using the name argument as follows.
In [18]: bs_age = MS([bs('age',
internal_knots=[25,40,60],
name='bs(age)')])
Xbs = bs_age.fit_transform(Wage)
M = sm.OLS(y, Xbs).fit()
summarize(M)| Out[18]: | coef | std err |
t | P> t | ||
|---|---|---|---|---|---|---|
| intercept | 60.494 | 9.460 | 6.394 | 0.000 | ||
| bs(age, | knots)[0] | 3.981 | 12.538 | 0.317 | 0.751 | |
| bs(age, | knots)[1] | 44.631 | 9.626 | 4.636 | 0.000 | |
| bs(age, | knots)[2] | 62.839 | 10.755 | 5.843 | 0.000 | |
| bs(age, | knots)[3] | 55.991 | 10.706 | 5.230 | 0.000 | |
| bs(age, | knots)[4] | 50.688 | 14.402 | 3.520 | 0.000 | |
| bs(age, | knots)[5] | 16.606 | 19.126 | 0.868 | 0.385 | |
Notice that there are 6 spline coefcients rather than 7. This is because, by default, bs() assumes intercept=False, since we typically have an overall intercept in the model. So it generates the spline basis with the given knots, and then discards one of the basis functions to account for the intercept.
We could also use the df (degrees of freedom) option to specify the complexity of the spline. We see above that with 3 knots, the spline basis has 6 columns or degrees of freedom. When we specify df=6 rather than the actual knots, bs() will produce a spline with 3 knots chosen at uniform quantiles of the training data. We can see these chosen knots most easily using Bspline() directly:
In [19]: BSpline(df=6).fit(age).internal_knots_Out[19]: array([33.75, 42.0, 51.0])When asking for six degrees of freedom, the transform chooses knots at ages 33.75, 42.0, and 51.0, which correspond to the 25th, 50th, and 75th percentiles of age.
When using B-splines we need not limit ourselves to cubic polynomials (i.e. degree=3). For instance, using degree=0 results in piecewise constant functions, as in our example with pd.qcut() above.
In [20]: bs_age0 = MS([bs(‘age’,
df=3,
degree=0)]).fit(Wage)
Xbs0 = bs_age0.transform(Wage)
summarize(sm.OLS(y, Xbs0).fit())| Out[20]: | coef | std err |
t | P> t | |||
|---|---|---|---|---|---|---|---|
| intercept | 94.158 | 1.478 | 63.687 | 0.0 | |||
| bs(age, | df=3, | degree=0)[0] | 22.349 | 2.152 | 10.388 | 0.0 | |
| bs(age, | df=3, | degree=0)[1] | 24.808 | 2.044 | 12.137 | 0.0 | |
| bs(age, | df=3, | degree=0)[2] | 22.781 | 2.087 | 10.917 | 0.0 |
This ft should be compared with cell [15] where we use qcut() to create four bins by cutting at the 25%, 50% and 75% quantiles of age. Since we specifed df=3 for degree-zero splines here, there will also be knots at the same three quantiles. Although the coefcients appear diferent, we see that this is a result of the diferent coding. For example, the frst coefcient is identical in both cases, and is the mean response in the frst bin. For the second coefcient, we have 94.158 + 22.349 = 116.507 ≈ 116.611, the latter being the mean in the second bin in cell [15]. Here the intercept is coded by a column of ones, so the second, third and fourth coefcients are increments for those bins. Why is the sum not exactly the same? It turns out that the qcut() uses ≤, while bs() uses < when deciding bin membership.
In order to ft a natural spline, we use the NaturalSpline() transform Natural with the corresponding helper Spline() ns(). Here we ft a natural spline with fve degrees of freedom (excluding the intercept) and plot the results.
In [21]: ns_age = MS([ns('age', df=5)]).fit(Wage)
M_ns = sm.OLS(y, ns_age.transform(Wage)).fit()
summarize(M_ns)| Out[21]: | coef | std err |
t | P> t | ||
|---|---|---|---|---|---|---|
| intercept | 60.475 | 4.708 | 12.844 | 0.000 | ||
| ns(age, | df=5)[0] | 61.527 | 4.709 | 13.065 | 0.000 | |
| ns(age, | df=5)[1] | 55.691 | 5.717 | 9.741 | 0.000 | |
| ns(age, | df=5)[2] | 46.818 | 4.948 | 9.463 | 0.000 | |
| ns(age, | df=5)[3] | 83.204 | 11.918 | 6.982 | 0.000 | |
| ns(age, | df=5)[4] | 6.877 | 9.484 | 0.725 | 0.468 | |
We now plot the natural spline using our plotting function.
In [22]: plot_wage_fit(age_df,
ns_age, ‘Natural spline, df=5’);
7.8.3 Smoothing Splines and GAMs
A smoothing spline is a special case of a GAM with squared-error loss and a single feature. To ft GAMs in Python we will use the pygam package pygam which can be installed via pip install pygam. The estimator LinearGAM() LinearGAM() uses squared-error loss. The GAM is specifed by associating each column of a model matrix with a particular smoothing operation: s for smoothing spline; l for linear, and f for factor or categorical variables. The argument 0 passed to s below indicates that this smoother will apply to the frst column of a feature matrix. Below, we pass it a matrix with a single column: X_age. The argument lam is the penalty parameter λ as discussed in Section 7.5.2.
In [23]: X_age = np.asarray(age).reshape((-1,1))
gam = LinearGAM(s_gam(0, lam=0.6))
gam.fit(X_age, y)318 7. Moving Beyond Linearity
Out[23]: LinearGAM(callbacks=[Deviance(), Diffs()], fit_intercept=True,
max_iter=100, scale=None, terms=s(0) + intercept, tol=0.0001,
verbose=False)The pygam library generally expects a matrix of features so we reshape age to be a matrix (a two-dimensional array) instead of a vector (i.e. a onedimensional array). The -1 in the call to the reshape() method tells numpy to impute the size of that dimension based on the remaining entries of the shape tuple.
Let’s investigate how the ft changes with the smoothing parameter lam. The function np.logspace() is similar to np.linspace() but spaces points np.logspace() evenly on the log-scale. Below we vary lam from 10−2 to 106.
In [24]: fig, ax = subplots(figsize=(8,8))
ax.scatter(age, y, facecolor='gray', alpha=0.5)
for lam in np.logspace(-2, 6, 5):
gam = LinearGAM(s_gam(0, lam=lam)).fit(X_age, y)
ax.plot(age_grid,
gam.predict(age_grid),
label='{:.1e}'.format(lam),
linewidth=3)
ax.set_xlabel('Age', fontsize=20)
ax.set_ylabel('Wage', fontsize=20);
ax.legend(title='$\lambda$');The pygam package can perform a search for an optimal smoothing parameter.
In [25]: gam_opt = gam.gridsearch(X_age, y)
ax.plot(age_grid,
gam_opt.predict(age_grid),
label='Grid search',
linewidth=4)
ax.legend()
figAlternatively, we can fx the degrees of freedom of the smoothing spline using a function included in the ISLP.pygam package. Below we fnd a value of λ that gives us roughly four degrees of freedom. We note here that these degrees of freedom include the unpenalized intercept and linear term of the smoothing spline, hence there are at least two degrees of freedom.
In [26]: age_term = gam.terms[0]
lam_4 = approx_lam(X_age, age_term, 4)
age_term.lam = lam_4
degrees_of_freedom(X_age, age_term)Out[26]: 4.000000100004728
Let’s vary the degrees of freedom in a similar plot to above. We choose the degrees of freedom as the desired degrees of freedom plus one to account for the fact that these smoothing splines always have an intercept term. Hence, a value of one for df is just a linear ft.
In [27]: fig, ax = subplots(figsize=(8,8))
ax.scatter(X_age,
y,facecolor='gray',
alpha=0.3)
for df in [1,3,4,8,15]:
lam = approx_lam(X_age, age_term, df+1)
age_term.lam = lam
gam.fit(X_age, y)
ax.plot(age_grid,
gam.predict(age_grid),
label='{:d}'.format(df),
linewidth=4)
ax.set_xlabel('Age', fontsize=20)
ax.set_ylabel('Wage', fontsize=20);
ax.legend(title='Degrees of freedom');Additive Models with Several Terms
The strength of generalized additive models lies in their ability to ft multivariate regression models with more fexibility than linear models. We demonstrate two approaches: the frst in a more manual fashion using natural splines and piecewise constant functions, and the second using the pygam package and smoothing splines.
We now ft a GAM by hand to predict wage using natural spline functions of year and age, treating education as a qualitative predictor, as in (7.16). Since this is just a big linear regression model using an appropriate choice of basis functions, we can simply do this using the sm.OLS() function.
We will build the model matrix in a more manual fashion here, since we wish to access the pieces separately when constructing partial dependence plots.
In [28]: ns_age = NaturalSpline(df=4).fit(age)
ns_year = NaturalSpline(df=5).fit(Wage['year'])
Xs = [ns_age.transform(age),
ns_year.transform(Wage['year']),
pd.get_dummies(Wage['education']).values]
X_bh = np.hstack(Xs)
gam_bh = sm.OLS(y, X_bh).fit()Here the function NaturalSpline() is the workhorse supporting the ns() helper function. We chose to use all columns of the indicator matrix for the categorical variable education, making an intercept redundant. Finally, we stacked the three component matrices horizontally to form the model matrix X_bh.
We now show how to construct partial dependence plots for each of the terms in our rudimentary GAM. We can do this by hand, given grids for age and year. We simply predict with new X matrices, fxing all but one of the features at a time.
In [29]: age_grid = np.linspace(age.min(),
age.max(),
100)
X_age_bh = X_bh.copy()[:100]
X_age_bh[:] = X_bh[:].mean(0)[None,:]
X_age_bh[:,:4] = ns_age.transform(age_grid)
preds = gam_bh.get_prediction(X_age_bh)
bounds_age = preds.conf_int(alpha=0.05)320 7. Moving Beyond Linearity
partial_age = preds.predicted_mean
center = partial_age.mean()
partial_age -= center
bounds_age -= center
fig, ax = subplots(figsize=(8,8))
ax.plot(age_grid, partial_age, 'b', linewidth=3)
ax.plot(age_grid, bounds_age[:,0], 'r--', linewidth=3)
ax.plot(age_grid, bounds_age[:,1], 'r--', linewidth=3)
ax.set_xlabel('Age')
ax.set_ylabel('Effect on wage')
ax.set_title('Partial dependence of age on wage', fontsize=20);Let’s explain in some detail what we did above. The idea is to create a new prediction matrix, where all but the columns belonging to age are constant (and set to their training-data means). The four columns for age are flled in with the natural spline basis evaluated at the 100 values in age_grid.
- We made a grid of length 100 in age, and created a matrix X_age_bh with 100 rows and the same number of columns as X_bh.
- We replaced every row of this matrix with the column means of the original.
- We then replace just the frst four columns representing age with the natural spline basis computed at the values in age_grid.
The remaining steps should by now be familiar.
We also look at the efect of year on wage; the process is the same.
In [30]: year_grid = np.linspace(2003, 2009, 100)year_grid = np.linspace(Wage['year'].min(),
Wage['year'].max(),
100)
X_year_bh = X_bh.copy()[:100]
X_year_bh[:] = X_bh[:].mean(0)[None,:]
X_year_bh[:,4:9] = ns_year.transform(year_grid)
preds = gam_bh.get_prediction(X_year_bh)
bounds_year = preds.conf_int(alpha=0.05)
partial_year = preds.predicted_mean
center = partial_year.mean()
partial_year -= center
bounds_year -= center
fig, ax = subplots(figsize=(8,8))
ax.plot(year_grid, partial_year , 'b', linewidth=3)
ax.plot(year_grid, bounds_year[:,0], 'r--', linewidth=3)
ax.plot(year_grid, bounds_year[:,1], 'r--', linewidth=3)
ax.set_xlabel('Year')
ax.set_ylabel('Effect on wage')
ax.set_title('Partial dependence of year on wage', fontsize=20);We now ft the model (7.16) using smoothing splines rather than natural splines. All of the terms in (7.16) are ft simultaneously, taking each other into account to explain the response. The pygam package only works with matrices, so we must convert the categorical series education to its array representation, which can be found with the cat.codes attribute of education. As year only has 7 unique values, we use only seven basis functions for it.
In [31]: gam_full = LinearGAM(s_gam(0) +
s_gam(1, n_splines=7) +
f_gam(2, lam=0))
Xgam = np.column_stack([age,
Wage['year'],
Wage['education'].cat.codes])
gam_full = gam_full.fit(Xgam, y)The two s_gam() terms result in smoothing spline fts, and use a default value for λ (lam=0.6), which is somewhat arbitrary. For the categorical term education, specifed using a f_gam() term, we specify lam=0 to avoid any shrinkage. We produce the partial dependence plot in age to see the efect of these choices.
The values for the plot are generated by the pygam package. We provide a plot_gam() function for partial-dependence plots in ISLP.pygam, which plot_gam() makes this job easier than in our last example with natural splines.
In [32]: fig, ax = subplots(figsize=(8,8))
plot_gam(gam_full, 0, ax=ax)
ax.set_xlabel('Age')
ax.set_ylabel('Effect on wage')
ax.set_title('Partial dependence of age on wage - default lam=0.6',
fontsize=20);We see that the function is somewhat wiggly. It is more natural to specify the df than a value for lam. We reft a GAM using four degrees of freedom each for age and year. Recall that the addition of one below takes into account the intercept of the smoothing spline.
In [33]: age_term = gam_full.terms[0]
age_term.lam = approx_lam(Xgam, age_term, df=4+1)
year_term = gam_full.terms[1]
year_term.lam = approx_lam(Xgam, year_term, df=4+1)
gam_full = gam_full.fit(Xgam, y)Note that updating age_term.lam above updates it in gam_full.terms[0] as well! Likewise for year_term.lam.
Repeating the plot for age, we see that it is much smoother. We also produce the plot for year.
In [34]: fig, ax = subplots(figsize=(8,8))
plot_gam(gam_full,
1,
ax=ax)
ax.set_xlabel('Year')
ax.set_ylabel('Effect on wage')
ax.set_title('Partial dependence of year on wage', fontsize=20)Finally we plot education, which is categorical. The partial dependence plot is diferent, and more suitable for the set of ftted constants for each level of this variable.
In [35]: fig, ax = subplots(figsize=(8, 8))
ax = plot_gam(gam_full, 2)
ax.set_xlabel('Education')
ax.set_ylabel('Effect on wage')322 7. Moving Beyond Linearity
ax.set_title('Partial dependence of wage on education',
fontsize=20);
ax.set_xticklabels(Wage['education'].cat.categories, fontsize=8);ANOVA Tests for Additive Models
In all of our models, the function of year looks rather linear. We can perform a series of ANOVA tests in order to determine which of these three models is best: a GAM that excludes year (M1), a GAM that uses a linear function of year (M2), or a GAM that uses a spline function of year (M3).
In [36]: gam_0 = LinearGAM(age_term + f_gam(2, lam=0))
gam_0.fit(Xgam, y)
gam_linear = LinearGAM(age_term +
l_gam(1, lam=0) +
f_gam(2, lam=0))
gam_linear.fit(Xgam, y)Out[36]: LinearGAM(callbacks=[Deviance(), Diffs()], fit_intercept=True,
max_iter=100, scale=None, terms=s(0) + l(1) + f(2) + intercept,
tol=0.0001, verbose=False)Notice our use of age_term in the expressions above. We do this because earlier we set the value for lam in this term to achieve four degrees of freedom.
To directly assess the efect of year we run an ANOVA on the three models ft above.
In [37]: anova_gam(gam_0, gam_linear, gam_full)Out[37]:
| deviance | df | deviance_diff | df_diff | F | pvalue | |
|---|---|---|---|---|---|---|
| 0 | 3714362.366 | 2991.004 | NaN | NaN | NaN | NaN |
| 1 | 3696745.823 | 2990.005 | 17616.543 | 0.999 | 14.265 | 0.002 |
| 2 | 3693142.930 | 2987.007 | 3602.894 | 2.998 | 0.972 | 0.436 |
We fnd that there is compelling evidence that a GAM with a linear function in year is better than a GAM that does not include year at all (p-value= 0.002). However, there is no evidence that a non-linear function of year is needed (p-value=0.435). In other words, based on the results of this ANOVA, M2 is preferred.
We can repeat the same process for age as well. We see there is very clear evidence that a non-linear term is required for age.
In [38]: gam_0 = LinearGAM(year_term +
f_gam(2, lam=0))
gam_linear = LinearGAM(l_gam(0, lam=0) +
year_term +
f_gam(2, lam=0))
gam_0.fit(Xgam, y)
gam_linear.fit(Xgam, y)
anova_gam(gam_0, gam_linear, gam_full)Out[38]: deviance df deviance_diff df_diff F pvalue
0 3975443.045 2991.001 NaN NaN NaN NaN
1 3850246.908 2990.001 125196.137 1.000 101.270 0.000
2 3693142.930 2987.007 157103.978 2.993 42.448 0.000There is a (verbose) summary() method for the GAM ft. (We do not reproduce it here.)
In [39]: gam_full.summary()
We can make predictions from gam objects, just like from lm objects, using the predict() method for the class gam. Here we make predictions on the training set.
In [40]: Yhat = gam_full.predict(Xgam)In order to ft a logistic regression GAM, we use LogisticGAM() from LogisticGAM() pygam.
In [41]: gam_logit = LogisticGAM(age_term +
l_gam(1, lam=0) +
f_gam(2, lam=0))
gam_logit.fit(Xgam, high_earn)Out[41]: LogisticGAM(callbacks=[Deviance(), Diffs(), Accuracy()],
fit_intercept=True, max_iter=100,terms=s(0) + l(1) + f(2) + intercept, tol=0.0001, verbose=False)In [42]: fig, ax = subplots(figsize=(8, 8))
ax = plot_gam(gam_logit, 2)
ax.set_xlabel('Education')
ax.set_ylabel('Effect on wage')
ax.set_title('Partial dependence of wage on education',
fontsize=20);
ax.set_xticklabels(Wage['education'].cat.categories, fontsize=8);The model seems to be very fat, with especially high error bars for the frst category. Let’s look at the data a bit more closely.
In [43]: pd.crosstab(Wage[‘high_earn’], Wage[‘education’])
We see that there are no high earners in the frst category of education, meaning that the model will have a hard time ftting. We will ft a logistic regression GAM excluding all observations falling into this category. This provides more sensible results.
To do so, we could subset the model matrix, though this will not remove the column from Xgam. While we can deduce which column corresponds to this feature, for reproducibility’s sake we reform the model matrix on this smaller subset.
In [44]: only_hs = Wage['education'] == '1. < HS Grad'
Wage_ = Wage.loc[∼only_hs]
Xgam_ = np.column_stack([Wage_['age'],
Wage_['year'],
Wage_['education'].cat.codes -1])
high_earn_ = Wage_['high_earn']324 7. Moving Beyond Linearity
In the second-to-last line above, we subtract one from the codes of the category, due to a bug in pygam. It just relabels the education values and hence has no efect on the ft.
We now ft the model.
In [45]: gam_logit_ = LogisticGAM(age_term +
year_term +
f_gam(2, lam=0))
gam_logit_.fit(Xgam_, high_earn_)Out[45]: LogisticGAM(callbacks=[Deviance(), Diffs(), Accuracy()],
fit_intercept=True, max_iter=100,
terms=s(0) + s(1) + f(2) + intercept, tol=0.0001, verbose=False)Let’s look at the efect of education, year and age on high earner status now that we’ve removed those observations.
In [46]: fig, ax = subplots(figsize=(8, 8))
ax = plot_gam(gam_logit_, 2)
ax.set_xlabel('Education')
ax.set_ylabel('Effect on wage')
ax.set_title('Partial dependence of high earner status on education
', fontsize=20);
ax.set_xticklabels(Wage['education'].cat.categories[1:],
fontsize=8);In [47]: fig, ax = subplots(figsize=(8, 8))
ax = plot_gam(gam_logit_, 1)
ax.set_xlabel('Year')
ax.set_ylabel('Effect on wage')
ax.set_title('Partial dependence of high earner status on year',
fontsize=20);In [48]: fig, ax = subplots(figsize=(8, 8))
ax = plot_gam(gam_logit_, 0)
ax.set_xlabel('Age')
ax.set_ylabel('Effect on wage')
ax.set_title('Partial dependence of high earner status on age',
fontsize=20);7.8.4 Local Regression
We illustrate the use of local regression using the lowess() function from lowess() sm.nonparametric. Some implementations of GAMs allow terms to be local regression operators; this is not the case in pygam.
Here we ft local linear regression models using spans of 0.2 and 0.5; that is, each neighborhood consists of 20% or 50% of the observations. As expected, using a span of 0.5 is smoother than 0.2.
In [49]: lowess = sm.nonparametric.lowess
fig, ax = subplots(figsize=(8,8))
ax.scatter(age, y, facecolor='gray', alpha=0.5)
for span in [0.2, 0.5]:
fitted = lowess(y,age,
frac=span,
xvals=age_grid)
ax.plot(age_grid,
fitted,
label='{:.1f}'.format(span),
linewidth=4)
ax.set_xlabel('Age', fontsize=20)
ax.set_ylabel('Wage', fontsize=20);
ax.legend(title='span', fontsize=15);7.9 Exercises
Conceptual
- It was mentioned in this chapter that a cubic regression spline with one knot at ξ can be obtained using a basis of the form x, x2, x3, (x − ξ)3 +, where (x − ξ)3 + = (x − ξ)3 if x > ξ and equals 0 otherwise. We will now show that a function of the form
\[f(x) = \beta\_0 + \beta\_1 x + \beta\_2 x^2 + \beta\_3 x^3 + \beta\_4 (x - \xi)\_+^3\]
is indeed a cubic regression spline, regardless of the values of β0, β1, β2, β3, β4.
- Find a cubic polynomial
\[f\_1(x) = a\_1 + b\_1 x + c\_1 x^2 + d\_1 x^3\]
such that f(x) = f1(x) for all x ≤ ξ. Express a1, b1, c1, d1 in terms of β0, β1, β2, β3, β4.
- Find a cubic polynomial
\[f\_2(x) = a\_2 + b\_2 x + c\_2 x^2 + d\_2 x^3\]
such that f(x) = f2(x) for all x > ξ. Express a2, b2, c2, d2 in terms of β0, β1, β2, β3, β4. We have now established that f(x) is a piecewise polynomial.
- Show that f1(ξ) = f2(ξ). That is, f(x) is continuous at ξ.
- Show that f′ 1(ξ) = f′ 2(ξ). That is, f′ (x) is continuous at ξ.
- Show that f′′ 1 (ξ) = f′′ 2 (ξ). That is, f′′(x) is continuous at ξ.
Therefore, f(x) is indeed a cubic spline.
Hint: Parts (d) and (e) of this problem require knowledge of singlevariable calculus. As a reminder, given a cubic polynomial
\[f\_1(x) = a\_1 + b\_1 x + c\_1 x^2 + d\_1 x^3,\]
the frst derivative takes the form
\[f\_1'(x) = b\_1 + 2c\_1x + 3d\_1x^2\]
and the second derivative takes the form
\[f\_1''(x) = 2c\_1 + 6d\_1x.\]
- Suppose that a curve gˆ is computed to smoothly ft a set of n points using the following formula:
\[ \hat{g} = \arg\min\_{g} \left( \sum\_{i=1}^{n} (y\_i - g(x\_i))^2 + \lambda \int \left[ g^{(m)}(x) \right]^2 dx \right), \]
where g(m) represents the mth derivative of g (and g(0) = g). Provide example sketches of gˆ in each of the following scenarios.
- λ = ∞, m = 0.
- λ = ∞, m = 1.
- λ = ∞, m = 2.
- λ = ∞, m = 3.
- λ = 0, m = 3.
- Suppose we ft a curve with basis functions b1(X) = X, b2(X) = (X − 1)2I(X ≥ 1). (Note that I(X ≥ 1) equals 1 for X ≥ 1 and 0 otherwise.) We ft the linear regression model
\[Y = \beta\_0 + \beta\_1 b\_1(X) + \beta\_2 b\_2(X) + \epsilon,\]
and obtain coefcient estimates βˆ0 = 1, βˆ1 = 1, βˆ2 = −2. Sketch the estimated curve between X = −2 and X = 2. Note the intercepts, slopes, and other relevant information.
- Suppose we ft a curve with basis functions b1(X) = I(0 ≤ X ≤ 2) − (X −1)I(1 ≤ X ≤ 2), b2(X)=(X −3)I(3 ≤ X ≤ 4) +I(4 < X ≤ 5). We ft the linear regression model
\[Y = \beta\_0 + \beta\_1 b\_1(X) + \beta\_2 b\_2(X) + \epsilon,\]
and obtain coefcient estimates βˆ0 = 1, βˆ1 = 1, βˆ2 = 3. Sketch the estimated curve between X = −2 and X = 6. Note the intercepts, slopes, and other relevant information.
- Consider two curves, gˆ1 and gˆ2, defned by
\[ \hat{g}\_1 = \arg\min\_g \left( \sum\_{i=1}^n (y\_i - g(x\_i))^2 + \lambda \int \left[ g^{(3)}(x) \right]^2 dx \right), \]
\[ \hat{g}\_2 = \arg\min\_g \left( \sum\_{i=1}^n (y\_i - g(x\_i))^2 + \lambda \int \left[ g^{(4)}(x) \right]^2 dx \right), \]
where g(m) represents the mth derivative of g.
- As λ → ∞, will gˆ1 or gˆ2 have the smaller training RSS?
- As λ → ∞, will gˆ1 or gˆ2 have the smaller test RSS?
- For λ = 0, will gˆ1 or gˆ2 have the smaller training and test RSS?
Applied
- In this exercise, you will further analyze the Wage data set considered throughout this chapter.
- Perform polynomial regression to predict wage using age. Use cross-validation to select the optimal degree d for the polynomial. What degree was chosen, and how does this compare to the results of hypothesis testing using ANOVA? Make a plot of the resulting polynomial ft to the data.
- Fit a step function to predict wage using age, and perform crossvalidation to choose the optimal number of cuts. Make a plot of the ft obtained.
- The Wage data set contains a number of other features not explored in this chapter, such as marital status (maritl), job class (jobclass), and others. Explore the relationships between some of these other predictors and wage, and use non-linear ftting techniques in order to ft fexible models to the data. Create plots of the results obtained, and write a summary of your fndings.
- Fit some of the non-linear models investigated in this chapter to the Auto data set. Is there evidence for non-linear relationships in this data set? Create some informative plots to justify your answer.
- This question uses the variables dis (the weighted mean of distances to fve Boston employment centers) and nox (nitrogen oxides concentration in parts per 10 million) from the Boston data. We will treat dis as the predictor and nox as the response.
- Use the poly() function from the ISLP.models module to ft a cubic polynomial regression to predict nox using dis. Report the regression output, and plot the resulting data and polynomial fts.
- Plot the polynomial fts for a range of diferent polynomial degrees (say, from 1 to 10), and report the associated residual sum of squares.
- Perform cross-validation or another approach to select the optimal degree for the polynomial, and explain your results.
- Use the bs() function from the ISLP.models module to ft a regression spline to predict nox using dis. Report the output for the ft using four degrees of freedom. How did you choose the knots? Plot the resulting ft.
- Now ft a regression spline for a range of degrees of freedom, and plot the resulting fts and report the resulting RSS. Describe the results obtained.
- Perform cross-validation or another approach in order to select the best degrees of freedom for a regression spline on this data. Describe your results.
- This question relates to the College data set.
- Split the data into a training set and a test set. Using out-of-state tuition as the response and the other variables as the predictors, perform forward stepwise selection on the training set in order to identify a satisfactory model that uses just a subset of the predictors.
- Fit a GAM on the training data, using out-of-state tuition as the response and the features selected in the previous step as the predictors. Plot the results, and explain your fndings.
- Evaluate the model obtained on the test set, and explain the results obtained.
- For which variables, if any, is there evidence of a non-linear relationship with the response?
- In Section 7.7, it was mentioned that GAMs are generally ft using a backftting approach. The idea behind backftting is actually quite simple. We will now explore backftting in the context of multiple linear regression.
Suppose that we would like to perform multiple linear regression, but we do not have software to do so. Instead, we only have software to perform simple linear regression. Therefore, we take the following iterative approach: we repeatedly hold all but one coefcient estimate fxed at its current value, and update only that coefcient estimate using a simple linear regression. The process is continued until convergence—that is, until the coefcient estimates stop changing.
We now try this out on a toy example.
- Generate a response Y and two predictors X1 and X2, with n = 100.
- Write a function simple_reg() that takes two arguments outcome and feature, fts a simple linear regression model with this outcome and feature, and returns the estimated intercept and slope.
- Initialize beta1 to take on a value of your choice. It does not matter what value you choose.
- Keeping beta1 fxed, use your function simple_reg() to ft the model:
Y − beta1 · X1 = β0 + β2X2 + ϵ.
Store the resulting values as beta0 and beta2.
- Keeping beta2 fxed, ft the model
Y − beta2 · X2 = β0 + β1X1 + ϵ.
Store the result as beta0 and beta1 (overwriting their previous values).
- Write a for loop to repeat (c) and (d) 1,000 times. Report the estimates of beta0, beta1, and beta2 at each iteration of the for loop. Create a plot in which each of these values is displayed, with beta0, beta1, and beta2.
- Compare your answer in (e) to the results of simply performing multiple linear regression to predict Y using X1 and X2. Use axline() method to overlay those multiple linear regression coefcient estimates on the plot obtained in (e).
- On this data set, how many backftting iterations were required in order to obtain a “good” approximation to the multiple regression coefcient estimates?
- This problem is a continuation of the previous exercise. In a toy example with p = 100, show that one can approximate the multiple linear regression coefcient estimates by repeatedly performing simple linear regression in a backftting procedure. How many backftting iterations are required in order to obtain a “good” approximation to the multiple regression coefcient estimates? Create a plot to justify your answer.
8 Tree-Based Methods

In this chapter, we describe tree-based methods for regression and classifcation. These involve stratifying or segmenting the predictor space into a number of simple regions. In order to make a prediction for a given observation, we typically use the mean or the mode response value for the training observations in the region to which it belongs. Since the set of splitting rules used to segment the predictor space can be summarized in
a tree, these types of approaches are known as decision tree methods. decision tree Tree-based methods are simple and useful for interpretation. However, they typically are not competitive with the best supervised learning approaches, such as those seen in Chapters 6 and 7, in terms of prediction accuracy. Hence in this chapter we also introduce bagging, random forests, boosting, and Bayesian additive regression trees. Each of these approaches involves producing multiple trees which are then combined to yield a single consensus prediction. We will see that combining a large number of trees can often result in dramatic improvements in prediction accuracy, at the expense of some loss in interpretation.
8.1 The Basics of Decision Trees
Decision trees can be applied to both regression and classifcation problems. We frst consider regression problems, and then move on to classifcation.
8.1.1 Regression Trees
In order to motivate regression trees, we begin with a simple example. regression
tree
© Springer Nature Switzerland AG 2023
G. James et al., An Introduction to Statistical Learning, Springer Texts in Statistics, https://doi.org/10.1007/978-3-031-38747-0\_8
FIGURE 8.1. For the Hitters data, a regression tree for predicting the log salary of a baseball player, based on the number of years that he has played in the major leagues and the number of hits that he made in the previous year. At a given internal node, the label (of the form Xj < tk) indicates the left-hand branch emanating from that split, and the right-hand branch corresponds to Xj ≥ tk. For instance, the split at the top of the tree results in two large branches. The left-hand branch corresponds to Years<4.5, and the right-hand branch corresponds to Years>=4.5. The tree has two internal nodes and three terminal nodes, or leaves. The number in each leaf is the mean of the response for the observations that fall there.
Predicting Baseball Players’ Salaries Using Regression Trees
We use the Hitters data set to predict a baseball player’s Salary based on Years (the number of years that he has played in the major leagues) and Hits (the number of hits that he made in the previous year). We frst remove observations that are missing Salary values, and log-transform Salary so that its distribution has more of a typical bell-shape. (Recall that Salary is measured in thousands of dollars.)
Figure 8.1 shows a regression tree ft to this data. It consists of a series of splitting rules, starting at the top of the tree. The top split assigns observations having Years<4.5 to the left branch.1 The predicted salary for these players is given by the mean response value for the players in the data set with Years<4.5. For such players, the mean log salary is 5.107, and so we make a prediction of e5.107 thousands of dollars, i.e. $165,174, for these players. Players with Years>=4.5 are assigned to the right branch, and then that group is further subdivided by Hits. Overall, the tree stratifes or segments the players into three regions of predictor space: players who have played for four or fewer years, players who have played for fve or more years and who made fewer than 118 hits last year, and players who have played for fve or more years and who made at least 118 hits last year. These three regions can be written as R1 ={X | Years<4.5}, R2 ={X | Years>=4.5, Hits<117.5}, and R3 ={X | Years>=4.5, Hits>=117.5}. Figure 8.2 illustrates
1Both Years and Hits are integers in these data; the function used to ft this tree labels the splits at the midpoint between two adjacent values.
FIGURE 8.2. The three-region partition for the Hitters data set from the regression tree illustrated in Figure 8.1.
the regions as a function of Years and Hits. The predicted salaries for these three groups are $1,000×e5.107 =$165,174, $1,000×e5.999 =$402,834, and $1,000×e6.740 =$845,346 respectively.
In keeping with the tree analogy, the regions R1, R2, and R3 are known as terminal nodes or leaves of the tree. As is the case for Figure 8.1, decision terminal trees are typically drawn upside down, in the sense that the leaves are at the bottom of the tree. The points along the tree where the predictor space is split are referred to as internal nodes. In Figure 8.1, the two internal internal node nodes are indicated by the text Years<4.5 and Hits<117.5. We refer to the segments of the trees that connect the nodes as branches. branch We might interpret the regression tree displayed in Figure 8.1 as follows:
node leaf
Years is the most important factor in determining Salary, and players with less experience earn lower salaries than more experienced players. Given that a player is less experienced, the number of hits that he made in the previous year seems to play little role in his salary. But among players who have been in the major leagues for fve or more years, the number of hits made in the previous year does afect salary, and players who made more hits last year tend to have higher salaries. The regression tree shown in Figure 8.1 is likely an over-simplifcation of the true relationship between Hits, Years, and Salary. However, it has advantages over other types of regression models (such as those seen in Chapters 3 and 6): it is easier to interpret, and has a nice graphical representation.
Prediction via Stratifcation of the Feature Space
We now discuss the process of building a regression tree. Roughly speaking, there are two steps.
- We divide the predictor space — that is, the set of possible values for X1, X2,…,Xp — into J distinct and non-overlapping regions, R1, R2,…,RJ .
334 8. Tree-Based Methods
- For every observation that falls into the region Rj , we make the same prediction, which is simply the mean of the response values for the training observations in Rj .
For instance, suppose that in Step 1 we obtain two regions, R1 and R2, and that the response mean of the training observations in the frst region is 10, while the response mean of the training observations in the second region is 20. Then for a given observation X = x, if x ∈ R1 we will predict a value of 10, and if x ∈ R2 we will predict a value of 20.
We now elaborate on Step 1 above. How do we construct the regions R1,…,RJ ? In theory, the regions could have any shape. However, we choose to divide the predictor space into high-dimensional rectangles, or boxes, for simplicity and for ease of interpretation of the resulting predictive model. The goal is to fnd boxes R1,…,RJ that minimize the RSS, given by
\[\sum\_{j=1}^{J} \sum\_{i \in R\_j} (y\_i - \hat{y}\_{R\_j})^2,\tag{8.1}\]
where yˆRj is the mean response for the training observations within the jth box. Unfortunately, it is computationally infeasible to consider every possible partition of the feature space into J boxes. For this reason, we take a top-down, greedy approach that is known as recursive binary splitting. The recursive approach is top-down because it begins at the top of the tree (at which point all observations belong to a single region) and then successively splits the predictor space; each split is indicated via two new branches further down on the tree. It is greedy because at each step of the tree-building process, the best split is made at that particular step, rather than looking ahead and picking a split that will lead to a better tree in some future step.
binary splitting
In order to perform recursive binary splitting, we frst select the predictor Xj and the cutpoint s such that splitting the predictor space into the regions {X|Xj < s} and {X|Xj ≥ s} leads to the greatest possible reduction in RSS. (The notation {X|Xj < s} means the region of predictor space in which Xj takes on a value less than s.) That is, we consider all predictors X1,…,Xp, and all possible values of the cutpoint s for each of the predictors, and then choose the predictor and cutpoint such that the resulting tree has the lowest RSS. In greater detail, for any j and s, we defne the pair of half-planes
\[R\_1(j, s) = \{X | X\_j < s\} \quad \text{and} \quad R\_2(j, s) = \{X | X\_j \ge s\},\tag{8.2}\]
and we seek the value of j and s that minimize the equation
\[\sum\_{\substack{i:\,x\_i \in R\_1(j,\mathfrak{s})}} (y\_i - \hat{y}\_{R\_1})^2 + \sum\_{\substack{i:\,x\_i \in R\_2(j,\mathfrak{s})}} (y\_i - \hat{y}\_{R\_2})^2,\tag{8.3}\]
where yˆR1 is the mean response for the training observations in R1(j, s), and yˆR2 is the mean response for the training observations in R2(j, s). Finding the values of j and s that minimize (8.3) can be done quite quickly, especially when the number of features p is not too large.
Next, we repeat the process, looking for the best predictor and best cutpoint in order to split the data further so as to minimize the RSS within
t4
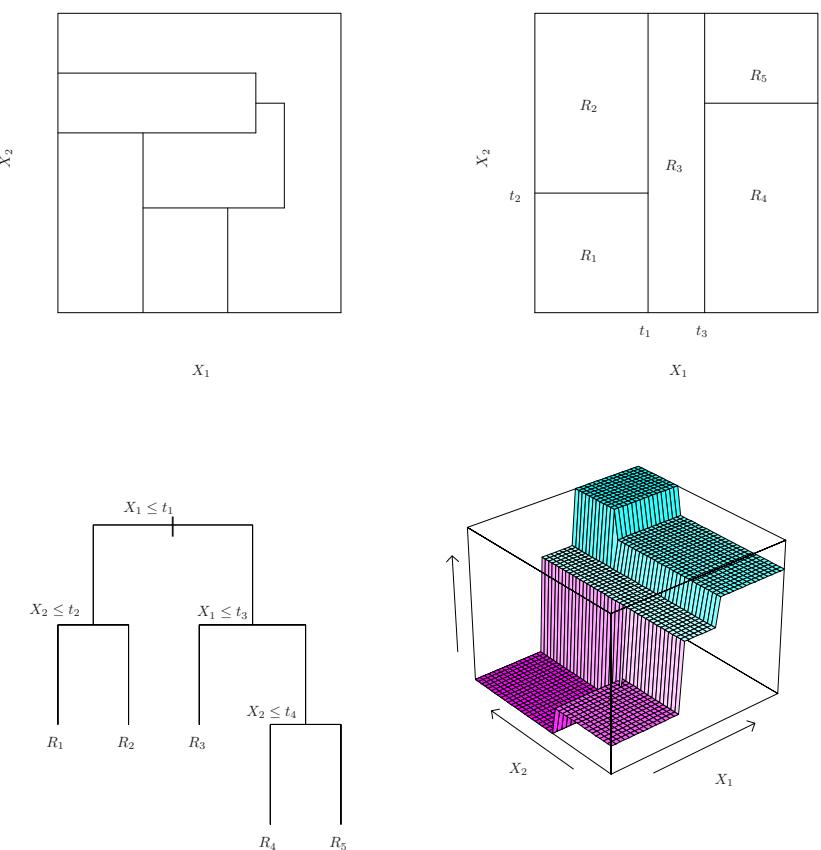
FIGURE 8.3. Top Left: A partition of two-dimensional feature space that could not result from recursive binary splitting. Top Right: The output of recursive binary splitting on a two-dimensional example. Bottom Left: A tree corresponding to the partition in the top right panel. Bottom Right: A perspective plot of the prediction surface corresponding to that tree.
each of the resulting regions. However, this time, instead of splitting the entire predictor space, we split one of the two previously identifed regions. We now have three regions. Again, we look to split one of these three regions further, so as to minimize the RSS. The process continues until a stopping criterion is reached; for instance, we may continue until no region contains more than fve observations.
Once the regions R1,…,RJ have been created, we predict the response for a given test observation using the mean of the training observations in the region to which that test observation belongs.
A fve-region example of this approach is shown in Figure 8.3.
Tree Pruning
The process described above may produce good predictions on the training set, but is likely to overft the data, leading to poor test set performance. This is because the resulting tree might be too complex. A smaller tree with fewer splits (that is, fewer regions R1,…,RJ ) might lead to lower variance and better interpretation at the cost of a little bias. One possible alternative to the process described above is to build the tree only so long as the decrease in the RSS due to each split exceeds some (high) threshold. This strategy will result in smaller trees, but is too short-sighted since a seemingly worthless split early on in the tree might be followed by a very good split—that is, a split that leads to a large reduction in RSS later on.
Therefore, a better strategy is to grow a very large tree T0, and then prune it back in order to obtain a subtree. How do we determine the best prune subtree way to prune the tree? Intuitively, our goal is to select a subtree that leads to the lowest test error rate. Given a subtree, we can estimate its test error using cross-validation or the validation set approach. However, estimating the cross-validation error for every possible subtree would be too cumbersome, since there is an extremely large number of possible subtrees. Instead, we need a way to select a small set of subtrees for consideration.
Cost complexity pruning—also known as weakest link pruning—gives us cost a way to do just this. Rather than considering every possible subtree, we consider a sequence of trees indexed by a nonnegative tuning parameter α. For each value of α there corresponds a subtree T ⊂ T0 such that
complexity pruning weakest link pruning
\[\sum\_{m=1}^{|T|} \sum\_{i:\ x\_i \in R\_m} (y\_i - \hat{y}\_{R\_m})^2 + \alpha |T| \tag{8.4}\]
is as small as possible. Here |T| indicates the number of terminal nodes of the tree T, Rm is the rectangle (i.e. the subset of predictor space) corresponding to the mth terminal node, and yˆRm is the predicted response associated with Rm—that is, the mean of the training observations in Rm. The tuning parameter α controls a trade-of between the subtree’s complexity and its ft to the training data. When α = 0, then the subtree T will simply equal T0, because then (8.4) just measures the training error. However, as α increases, there is a price to pay for having a tree with many terminal nodes, and so the quantity (8.4) will tend to be minimized for a smaller subtree. Equation 8.4 is reminiscent of the lasso (6.7) from Chapter 6, in which a similar formulation was used in order to control the complexity of a linear model.
It turns out that as we increase α from zero in (8.4), branches get pruned from the tree in a nested and predictable fashion, so obtaining the whole sequence of subtrees as a function of α is easy. We can select a value of α using a validation set or using cross-validation. We then return to the full data set and obtain the subtree corresponding to α. This process is summarized in Algorithm 8.1.
Figures 8.4 and 8.5 display the results of ftting and pruning a regression tree on the Hitters data, using nine of the features. First, we randomly divided the data set in half, yielding 132 observations in the training set and 131 observations in the test set. We then built a large regression tree on the training data and varied α in (8.4) in order to create subtrees with diferent numbers of terminal nodes. Finally, we performed six-fold crossvalidation in order to estimate the cross-validated MSE of the trees as
Algorithm 8.1 Building a Regression Tree
- Use recursive binary splitting to grow a large tree on the training data, stopping only when each terminal node has fewer than some minimum number of observations.
- Apply cost complexity pruning to the large tree in order to obtain a sequence of best subtrees, as a function of α.
- Use K-fold cross-validation to choose α. That is, divide the training observations into K folds. For each k = 1,…,K:
- Repeat Steps 1 and 2 on all but the kth fold of the training data.
- Evaluate the mean squared prediction error on the data in the left-out kth fold, as a function of α.
Average the results for each value of α, and pick α to minimize the average error.
- Return the subtree from Step 2 that corresponds to the chosen value of α.
a function of α. (We chose to perform six-fold cross-validation because 132 is an exact multiple of six.) The unpruned regression tree is shown in Figure 8.4. The green curve in Figure 8.5 shows the CV error as a function of the number of leaves,2 while the orange curve indicates the test error. Also shown are standard error bars around the estimated errors. For reference, the training error curve is shown in black. The CV error is a reasonable approximation of the test error: the CV error takes on its minimum for a three-node tree, while the test error also dips down at the three-node tree (though it takes on its lowest value at the ten-node tree). The pruned tree containing three terminal nodes is shown in Figure 8.1.
8.1.2 Classifcation Trees
A classifcation tree is very similar to a regression tree, except that it is classifcation tree used to predict a qualitative response rather than a quantitative one. Recall that for a regression tree, the predicted response for an observation is given by the mean response of the training observations that belong to the same terminal node. In contrast, for a classifcation tree, we predict that each observation belongs to the most commonly occurring class of training observations in the region to which it belongs. In interpreting the results of a classifcation tree, we are often interested not only in the class prediction corresponding to a particular terminal node region, but also in the class proportions among the training observations that fall into that region.
The task of growing a classifcation tree is quite similar to the task of growing a regression tree. Just as in the regression setting, we use recursive
2Although CV error is computed as a function of α, it is convenient to display the result as a function of |T|, the number of leaves; this is based on the relationship between α and |T| in the original tree grown to all the training data.
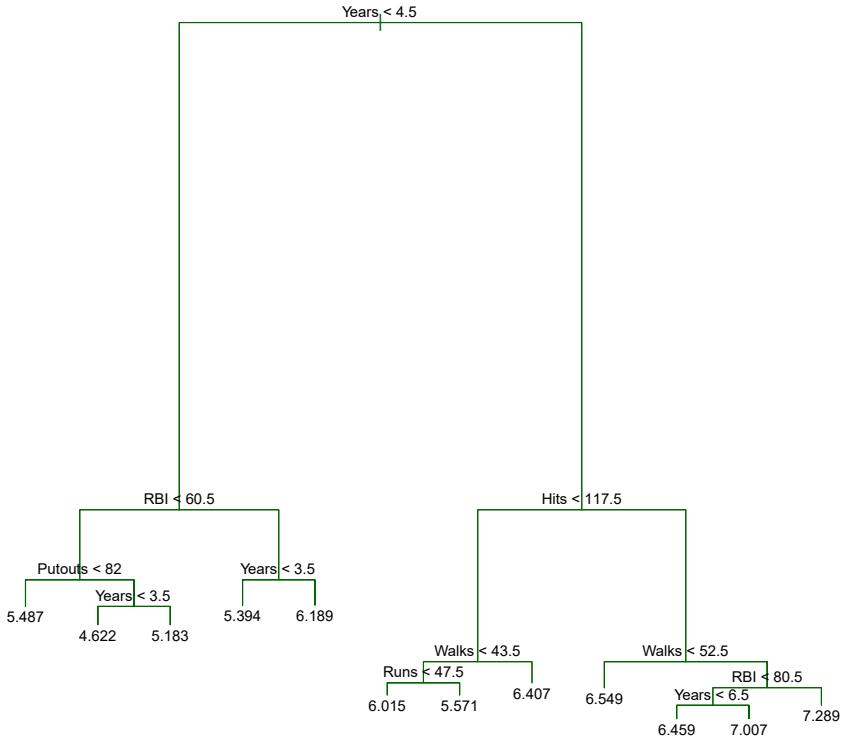
FIGURE 8.4. Regression tree analysis for the Hitters data. The unpruned tree that results from top-down greedy splitting on the training data is shown.
binary splitting to grow a classifcation tree. However, in the classifcation setting, RSS cannot be used as a criterion for making the binary splits. A natural alternative to RSS is the classifcation error rate. Since we plan classifcation error rate to assign an observation in a given region to the most commonly occurring class of training observations in that region, the classifcation error rate is simply the fraction of the training observations in that region that do not belong to the most common class:
\[\text{classification}\\ \text{error rate}\]
\[E = 1 - \max\_{k} (\hat{p}\_{mk}).\tag{8.5}\]
Here pˆmk represents the proportion of training observations in the mth region that are from the kth class. However, it turns out that classifcation error is not sufciently sensitive for tree-growing, and in practice two other measures are preferable.
The Gini index is defned by Gini index
\[G = \sum\_{k=1}^{K} \hat{p}\_{mk} (1 - \hat{p}\_{mk}),\tag{8.6}\]
a measure of total variance across the K classes. It is not hard to see that the Gini index takes on a small value if all of the pˆmk’s are close to zero or one. For this reason the Gini index is referred to as a measure of
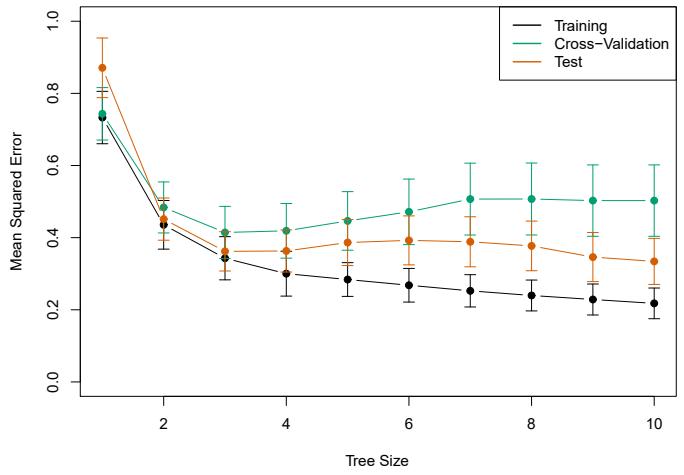
FIGURE 8.5. Regression tree analysis for the Hitters data. The training, cross-validation, and test MSE are shown as a function of the number of terminal nodes in the pruned tree. Standard error bands are displayed. The minimum cross-validation error occurs at a tree size of three.
node purity—a small value indicates that a node contains predominantly observations from a single class.
An alternative to the Gini index is entropy, given by entropy
\[D = -\sum\_{k=1}^{K} \hat{p}\_{mk} \log \hat{p}\_{mk}.\tag{8.7}\]
Since 0 ≤ pˆmk ≤ 1, it follows that 0 ≤ −pˆmk log ˆpmk. One can show that the entropy will take on a value near zero if the pˆmk’s are all near zero or near one. Therefore, like the Gini index, the entropy will take on a small value if the mth node is pure. In fact, it turns out that the Gini index and the entropy are quite similar numerically.
When building a classifcation tree, either the Gini index or the entropy are typically used to evaluate the quality of a particular split, since these two approaches are more sensitive to node purity than is the classifcation error rate. Any of these three approaches might be used when pruning the tree, but the classifcation error rate is preferable if prediction accuracy of the fnal pruned tree is the goal.
Figure 8.6 shows an example on the Heart data set. These data contain a binary outcome HD for 303 patients who presented with chest pain. An outcome value of Yes indicates the presence of heart disease based on an angiographic test, while No means no heart disease. There are 13 predictors including Age, Sex, Chol (a cholesterol measurement), and other heart and lung function measurements. Cross-validation results in a tree with six terminal nodes.
In our discussion thus far, we have assumed that the predictor variables take on continuous values. However, decision trees can be constructed even in the presence of qualitative predictor variables. For instance, in the Heart data, some of the predictors, such as Sex, Thal (Thallium stress test),
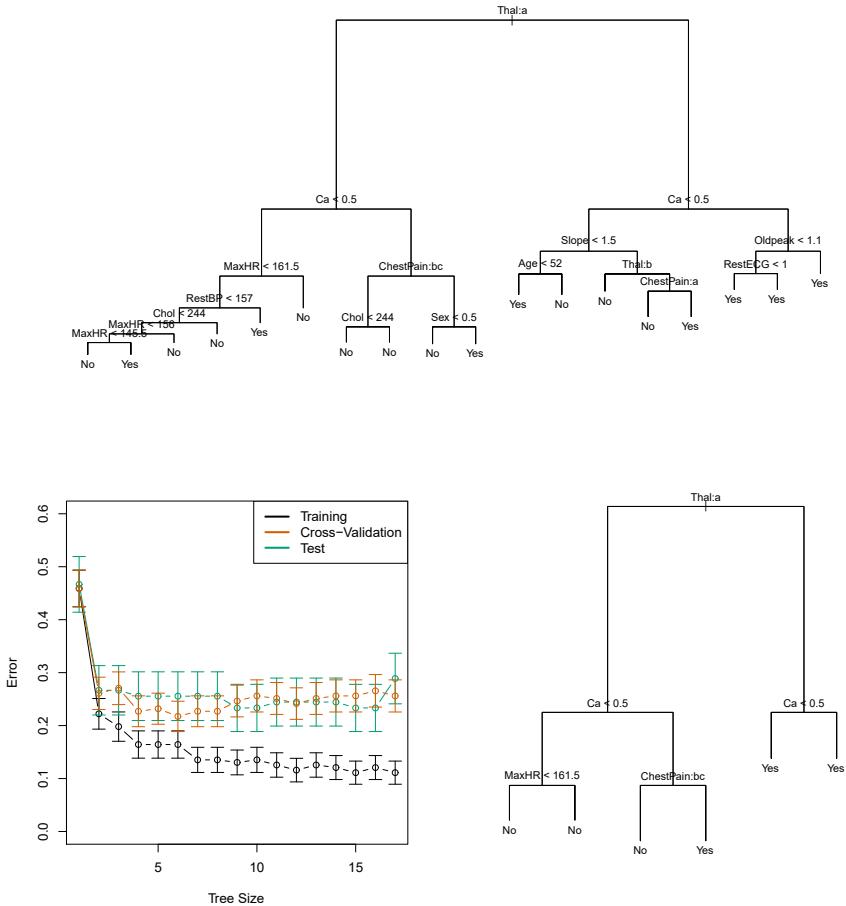
FIGURE 8.6. Heart data. Top: The unpruned tree. Bottom Left: Cross-validation error, training, and test error, for diferent sizes of the pruned tree. Bottom Right: The pruned tree corresponding to the minimal cross-validation error.
and ChestPain, are qualitative. Therefore, a split on one of these variables amounts to assigning some of the qualitative values to one branch and assigning the remaining to the other branch. In Figure 8.6, some of the internal nodes correspond to splitting qualitative variables. For instance, the top internal node corresponds to splitting Thal. The text Thal:a indicates that the left-hand branch coming out of that node consists of observations with the frst value of the Thal variable (normal), and the right-hand node consists of the remaining observations (fxed or reversible defects). The text ChestPain:bc two splits down the tree on the left indicates that the left-hand branch coming out of that node consists of observations with the second and third values of the ChestPain variable, where the possible values are typical angina, atypical angina, non-anginal pain, and asymptomatic.
Figure 8.6 has a surprising characteristic: some of the splits yield two terminal nodes that have the same predicted value. For instance, consider the split RestECG<1 near the bottom right of the unpruned tree. Regardless of the value of RestECG, a response value of Yes is predicted for those observations. Why, then, is the split performed at all? The split is performed because it leads to increased node purity. That is, all 9 of the observations corresponding to the right-hand leaf have a response value of Yes, whereas 7/11 of those corresponding to the left-hand leaf have a response value of Yes. Why is node purity important? Suppose that we have a test observation that belongs to the region given by that right-hand leaf. Then we can be pretty certain that its response value is Yes. In contrast, if a test observation belongs to the region given by the left-hand leaf, then its response value is probably Yes, but we are much less certain. Even though the split RestECG<1 does not reduce the classifcation error, it improves the Gini index and the entropy, which are more sensitive to node purity.
8.1.3 Trees Versus Linear Models
Regression and classifcation trees have a very diferent favor from the more classical approaches for regression and classifcation presented in Chapters 3 and 4. In particular, linear regression assumes a model of the form
\[f(X) = \beta\_0 + \sum\_{j=1}^{p} X\_j \beta\_j,\tag{8.8}\]
whereas regression trees assume a model of the form
\[f(X) = \sum\_{m=1}^{M} c\_m \cdot 1\_{\{X \in R\_m\}}\tag{8.9}\]
where R1,…,RM represent a partition of feature space, as in Figure 8.3.
Which model is better? It depends on the problem at hand. If the relationship between the features and the response is well approximated by a linear model as in (8.8), then an approach such as linear regression will likely work well, and will outperform a method such as a regression tree that does not exploit this linear structure. If instead there is a highly nonlinear and complex relationship between the features and the response as indicated by model (8.9), then decision trees may outperform classical approaches. An illustrative example is displayed in Figure 8.7. The relative performances of tree-based and classical approaches can be assessed by estimating the test error, using either cross-validation or the validation set approach (Chapter 5).
Of course, other considerations beyond simply test error may come into play in selecting a statistical learning method; for instance, in certain settings, prediction using a tree may be preferred for the sake of interpretability and visualization.
8.1.4 Advantages and Disadvantages of Trees
Decision trees for regression and classifcation have a number of advantages over the more classical approaches seen in Chapters 3 and 4:
▲ Trees are very easy to explain to people. In fact, they are even easier to explain than linear regression!
FIGURE 8.7. Top Row: A two-dimensional classifcation example in which the true decision boundary is linear, and is indicated by the shaded regions. A classical approach that assumes a linear boundary (left) will outperform a decision tree that performs splits parallel to the axes (right). Bottom Row: Here the true decision boundary is non-linear. Here a linear model is unable to capture the true decision boundary (left), whereas a decision tree is successful (right).
- ▲ Some people believe that decision trees more closely mirror human decision-making than do the regression and classifcation approaches seen in previous chapters.
- ▲ Trees can be displayed graphically, and are easily interpreted even by a non-expert (especially if they are small).
- ▲ Trees can easily handle qualitative predictors without the need to create dummy variables.
- ▼ Unfortunately, trees generally do not have the same level of predictive accuracy as some of the other regression and classifcation approaches seen in this book.
- ▼ Additionally, trees can be very non-robust. In other words, a small change in the data can cause a large change in the fnal estimated tree.
However, by aggregating many decision trees, using methods like bagging, random forests, and boosting, the predictive performance of trees can be substantially improved. We introduce these concepts in the next section.
8.2 Bagging, Random Forests, Boosting, and Bayesian Additive Regression Trees
An ensemble method is an approach that combines many simple “building ensemble block” models in order to obtain a single and potentially very powerful model. These simple building block models are sometimes known as weak
learners, since they may lead to mediocre predictions on their own. weak We will now discuss bagging, random forests, boosting, and Bayesian learners additive regression trees. These are ensemble methods for which the simple building block is a regression or a classifcation tree.
8.2.1 Bagging
The bootstrap, introduced in Chapter 5, is an extremely powerful idea. It is used in many situations in which it is hard or even impossible to directly compute the standard deviation of a quantity of interest. We see here that the bootstrap can be used in a completely diferent context, in order to improve statistical learning methods such as decision trees.
The decision trees discussed in Section 8.1 sufer from high variance. This means that if we split the training data into two parts at random, and ft a decision tree to both halves, the results that we get could be quite diferent. In contrast, a procedure with low variance will yield similar results if applied repeatedly to distinct data sets; linear regression tends to have low variance, if the ratio of n to p is moderately large. Bootstrap aggregation, or bagging, is a general-purpose procedure for reducing the bagging variance of a statistical learning method; we introduce it here because it is particularly useful and frequently used in the context of decision trees.
Recall that given a set of n independent observations Z1,…,Zn, each with variance σ2, the variance of the mean Z¯ of the observations is given by σ2/n. In other words, averaging a set of observations reduces variance. Hence a natural way to reduce the variance and increase the test set accuracy of a statistical learning method is to take many training sets from the population, build a separate prediction model using each training set, and average the resulting predictions. In other words, we could calculate ˆf 1(x), ˆf 2(x),…, ˆf B(x) using B separate training sets, and average them in order to obtain a single low-variance statistical learning model, given by
\[\hat{f}\_{\text{avg}}(x) = \frac{1}{B} \sum\_{b=1}^{B} \hat{f}^b(x).\]
Of course, this is not practical because we generally do not have access to multiple training sets. Instead, we can bootstrap, by taking repeated samples from the (single) training data set. In this approach we generate B diferent bootstrapped training data sets. We then train our method on the bth bootstrapped training set in order to get ˆf ∗b(x), and fnally average all the predictions, to obtain
\[\hat{f}\_{\text{bag}}(x) = \frac{1}{B} \sum\_{b=1}^{B} \hat{f}^{\*b}(x).\]
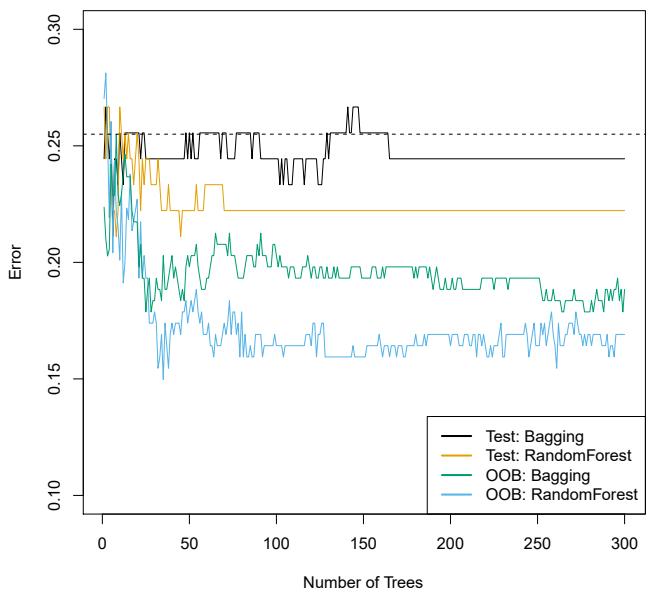
FIGURE 8.8. Bagging and random forest results for the Heart data. The test error (black and orange) is shown as a function of B, the number of bootstrapped training sets used. Random forests were applied with m = √p. The dashed line indicates the test error resulting from a single classifcation tree. The green and blue traces show the OOB error, which in this case is — by chance — considerably lower.
This is called bagging.
While bagging can improve predictions for many regression methods, it is particularly useful for decision trees. To apply bagging to regression trees, we simply construct B regression trees using B bootstrapped training sets, and average the resulting predictions. These trees are grown deep, and are not pruned. Hence each individual tree has high variance, but low bias. Averaging these B trees reduces the variance. Bagging has been demonstrated to give impressive improvements in accuracy by combining together hundreds or even thousands of trees into a single procedure.
Thus far, we have described the bagging procedure in the regression context, to predict a quantitative outcome Y . How can bagging be extended to a classifcation problem where Y is qualitative? In that situation, there are a few possible approaches, but the simplest is as follows. For a given test observation, we can record the class predicted by each of the B trees, and take a majority vote: the overall prediction is the most commonly occurring majority vote class among the B predictions.
Figure 8.8 shows the results from bagging trees on the Heart data. The test error rate is shown as a function of B, the number of trees constructed using bootstrapped training data sets. We see that the bagging test error rate is slightly lower in this case than the test error rate obtained from a single tree. The number of trees B is not a critical parameter with bagging; using a very large value of B will not lead to overftting. In practice we use a value of B sufciently large that the error has settled down. Using B = 100 is sufcient to achieve good performance in this example.
Out-of-Bag Error Estimation
It turns out that there is a very straightforward way to estimate the test error of a bagged model, without the need to perform cross-validation or the validation set approach. Recall that the key to bagging is that trees are repeatedly ft to bootstrapped subsets of the observations. One can show that on average, each bagged tree makes use of around two-thirds of the observations.3 The remaining one-third of the observations not used to ft a given bagged tree are referred to as the out-of-bag (OOB) observations. We out-of-bag can predict the response for the ith observation using each of the trees in which that observation was OOB. This will yield around B/3 predictions for the ith observation. In order to obtain a single prediction for the ith observation, we can average these predicted responses (if regression is the goal) or can take a majority vote (if classifcation is the goal). This leads to a single OOB prediction for the ith observation. An OOB prediction can be obtained in this way for each of the n observations, from which the overall OOB MSE (for a regression problem) or classifcation error (for a classifcation problem) can be computed. The resulting OOB error is a valid estimate of the test error for the bagged model, since the response for each observation is predicted using only the trees that were not ft using that observation. Figure 8.8 displays the OOB error on the Heart data. It can be shown that with B sufciently large, OOB error is virtually equivalent to leave-one-out cross-validation error. The OOB approach for estimating the test error is particularly convenient when performing bagging on large data sets for which cross-validation would be computationally onerous.
Variable Importance Measures
As we have discussed, bagging typically results in improved accuracy over prediction using a single tree. Unfortunately, however, it can be difcult to interpret the resulting model. Recall that one of the advantages of decision trees is the attractive and easily interpreted diagram that results, such as the one displayed in Figure 8.1. However, when we bag a large number of trees, it is no longer possible to represent the resulting statistical learning procedure using a single tree, and it is no longer clear which variables are most important to the procedure. Thus, bagging improves prediction accuracy at the expense of interpretability.
Although the collection of bagged trees is much more difcult to interpret than a single tree, one can obtain an overall summary of the importance of each predictor using the RSS (for bagging regression trees) or the Gini index (for bagging classifcation trees). In the case of bagging regression trees, we can record the total amount that the RSS (8.1) is decreased due to splits over a given predictor, averaged over all B trees. A large value indicates an important predictor. Similarly, in the context of bagging classifcation
3This relates to Exercise 2 of Chapter 5.
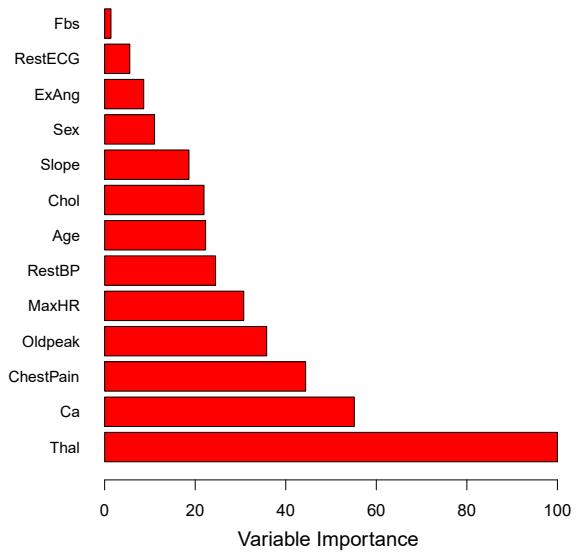
FIGURE 8.9. A variable importance plot for the Heart data. Variable importance is computed using the mean decrease in Gini index, and expressed relative to the maximum.
trees, we can add up the total amount that the Gini index (8.6) is decreased by splits over a given predictor, averaged over all B trees.
A graphical representation of the variable importances in the Heart data variable importance is shown in Figure 8.9. We see the mean decrease in Gini index for each variable, relative to the largest. The variables with the largest mean decrease in Gini index are Thal, Ca, and ChestPain.
8.2.2 Random Forests
Random forests provide an improvement over bagged trees by way of a random forest small tweak that decorrelates the trees. As in bagging, we build a number of decision trees on bootstrapped training samples. But when building these decision trees, each time a split in a tree is considered, a random sample of m predictors is chosen as split candidates from the full set of p predictors. The split is allowed to use only one of those m predictors. A fresh sample of m predictors is taken at each split, and typically we choose m ≈ √p—that is, the number of predictors considered at each split is approximately equal to the square root of the total number of predictors (4 out of the 13 for the Heart data).
In other words, in building a random forest, at each split in the tree, the algorithm is not even allowed to consider a majority of the available predictors. This may sound crazy, but it has a clever rationale. Suppose that there is one very strong predictor in the data set, along with a number of other moderately strong predictors. Then in the collection of bagged trees, most or all of the trees will use this strong predictor in the top split. Consequently, all of the bagged trees will look quite similar to each other. Hence the predictions from the bagged trees will be highly correlated. Unfortunately, averaging many highly correlated quantities does not lead to as large of a reduction in variance as averaging many uncorrelated quantities. In particular, this means that bagging will not lead to a substantial reduction in variance over a single tree in this setting.
Random forests overcome this problem by forcing each split to consider only a subset of the predictors. Therefore, on average (p − m)/p of the splits will not even consider the strong predictor, and so other predictors will have more of a chance. We can think of this process as decorrelating the trees, thereby making the average of the resulting trees less variable and hence more reliable.
The main diference between bagging and random forests is the choice of predictor subset size m. For instance, if a random forest is built using m = p, then this amounts simply to bagging. On the Heart data, random forests using m = √p leads to a reduction in both test error and OOB error over bagging (Figure 8.8).
Using a small value of m in building a random forest will typically be helpful when we have a large number of correlated predictors. We applied random forests to a high-dimensional biological data set consisting of expression measurements of 4,718 genes measured on tissue samples from 349 patients. There are around 20,000 genes in humans, and individual genes have diferent levels of activity, or expression, in particular cells, tissues, and biological conditions. In this data set, each of the patient samples has a qualitative label with 15 diferent levels: either normal or 1 of 14 diferent types of cancer. Our goal was to use random forests to predict cancer type based on the 500 genes that have the largest variance in the training set. We randomly divided the observations into a training and a test set, and applied random forests to the training set for three diferent values of the number of splitting variables m. The results are shown in Figure 8.10. The error rate of a single tree is 45.7 %, and the null rate is 75.4 %. 4 We see that using 400 trees is sufcient to give good performance, and that the choice m = √p gave a small improvement in test error over bagging (m = p) in this example. As with bagging, random forests will not overft if we increase B, so in practice we use a value of B sufciently large for the error rate to have settled down.
8.2.3 Boosting
We now discuss boosting, yet another approach for improving the predic- boosting tions resulting from a decision tree. Like bagging, boosting is a general approach that can be applied to many statistical learning methods for regression or classifcation. Here we restrict our discussion of boosting to the context of decision trees.
Recall that bagging involves creating multiple copies of the original training data set using the bootstrap, ftting a separate decision tree to each copy, and then combining all of the trees in order to create a single predic-
4The null rate results from simply classifying each observation to the dominant class overall, which is in this case the normal class.
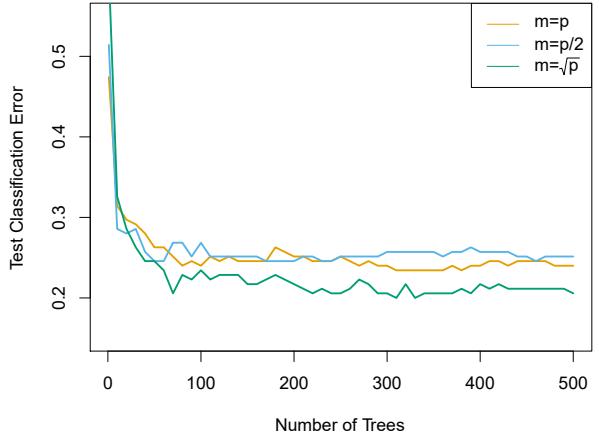
FIGURE 8.10. Results from random forests for the 15-class gene expression data set with p = 500 predictors. The test error is displayed as a function of the number of trees. Each colored line corresponds to a diferent value of m, the number of predictors available for splitting at each interior tree node. Random forests (m<p) lead to a slight improvement over bagging (m = p). A single classifcation tree has an error rate of 45.7 %.
tive model. Notably, each tree is built on a bootstrap data set, independent of the other trees. Boosting works in a similar way, except that the trees are grown sequentially: each tree is grown using information from previously grown trees. Boosting does not involve bootstrap sampling; instead each tree is ft on a modifed version of the original data set.
Consider frst the regression setting. Like bagging, boosting involves combining a large number of decision trees, ˆf 1,…, ˆf B. Boosting is described in Algorithm 8.2.
What is the idea behind this procedure? Unlike ftting a single large decision tree to the data, which amounts to ftting the data hard and potentially overftting, the boosting approach instead learns slowly. Given the current model, we ft a decision tree to the residuals from the model. That is, we ft a tree using the current residuals, rather than the outcome Y , as the response. We then add this new decision tree into the ftted function in order to update the residuals. Each of these trees can be rather small, with just a few terminal nodes, determined by the parameter d in the algorithm. By ftting small trees to the residuals, we slowly improve ˆf in areas where it does not perform well. The shrinkage parameter λ slows the process down even further, allowing more and diferent shaped trees to attack the residuals. In general, statistical learning approaches that learn slowly tend to perform well. Note that in boosting, unlike in bagging, the construction of each tree depends strongly on the trees that have already been grown.
We have just described the process of boosting regression trees. Boosting classifcation trees proceeds in a similar but slightly more complex way, and the details are omitted here.
Algorithm 8.2 Boosting for Regression Trees
- Set ˆf(x)=0 and ri = yi for all i in the training set.
- For b = 1, 2,…,B, repeat:
- Fit a tree ˆf b with d splits (d + 1 terminal nodes) to the training data (X, r).
- Update ˆf by adding in a shrunken version of the new tree:
\[ \hat{f}(x) \leftarrow \hat{f}(x) + \lambda \hat{f}^b(x). \tag{8.10} \]
- Update the residuals,
\[r\_i \gets r\_i - \lambda \hat{f}^b(x\_i). \tag{8.11}\]
- Output the boosted model,
\[\hat{f}(x) = \sum\_{b=1}^{B} \lambda \hat{f}^b(x). \tag{8.12}\]
Boosting has three tuning parameters:
- The number of trees B. Unlike bagging and random forests, boosting can overft if B is too large, although this overftting tends to occur slowly if at all. We use cross-validation to select B.
- The shrinkage parameter λ, a small positive number. This controls the rate at which boosting learns. Typical values are 0.01 or 0.001, and the right choice can depend on the problem. Very small λ can require using a very large value of B in order to achieve good performance.
- The number d of splits in each tree, which controls the complexity of the boosted ensemble. Often d = 1 works well, in which case each tree is a stump, consisting of a single split. In this case, the boosted stump ensemble is ftting an additive model, since each term involves only a single variable. More generally d is the interaction depth, and controls interaction depth the interaction order of the boosted model, since d splits can involve at most d variables.
In Figure 8.11, we applied boosting to the 15-class cancer gene expression data set, in order to develop a classifer that can distinguish the normal class from the 14 cancer classes. We display the test error as a function of the total number of trees and the interaction depth d. We see that simple stumps with an interaction depth of one perform well if enough of them are included. This model outperforms the depth-two model, and both outperform a random forest. This highlights one diference between boosting and random forests: in boosting, because the growth of a particular tree takes into account the other trees that have already been grown, smaller
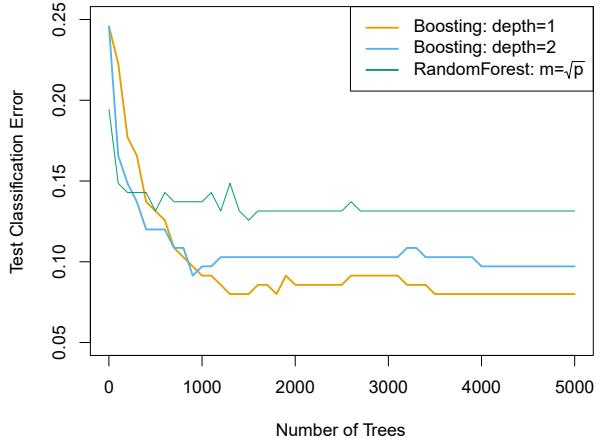
FIGURE 8.11. Results from performing boosting and random forests on the 15-class gene expression data set in order to predict cancer versus normal. The test error is displayed as a function of the number of trees. For the two boosted models, λ = 0.01. Depth-1 trees slightly outperform depth-2 trees, and both outperform the random forest, although the standard errors are around 0.02, making none of these diferences signifcant. The test error rate for a single tree is 24 %.
trees are typically sufcient. Using smaller trees can aid in interpretability as well; for instance, using stumps leads to an additive model.
8.2.4 Bayesian Additive Regression Trees
Finally, we discuss Bayesian additive regression trees (BART), another en- Bayesian semble method that uses decision trees as its building blocks. For simplicity, we present BART for regression (as opposed to classifcation).
Recall that bagging and random forests make predictions from an average of regression trees, each of which is built using a random sample of data and/or predictors. Each tree is built separately from the others. By contrast, boosting uses a weighted sum of trees, each of which is constructed by ftting a tree to the residual of the current ft. Thus, each new tree attempts to capture signal that is not yet accounted for by the current set of trees. BART is related to both approaches: each tree is constructed in a random manner as in bagging and random forests, and each tree tries to capture signal not yet accounted for by the current model, as in boosting. The main novelty in BART is the way in which new trees are generated.
Before we introduce the BART algorithm, we defne some notation. We let K denote the number of regression trees, and B the number of iterations for which the BART algorithm will be run. The notation ˆf b k(x) represents the prediction at x for the kth regression tree used in the bth iteration. At the end of each iteration, the K trees from that iteration will be summed, i.e. ˆf b(x) = #K k=1 ˆf b k(x) for b = 1,…,B.
In the frst iteration of the BART algorithm, all trees are initialized to have a single root node, with ˆf 1 k (x) = 1 nK #n i=1 yi, the mean of the response
additive regression trees
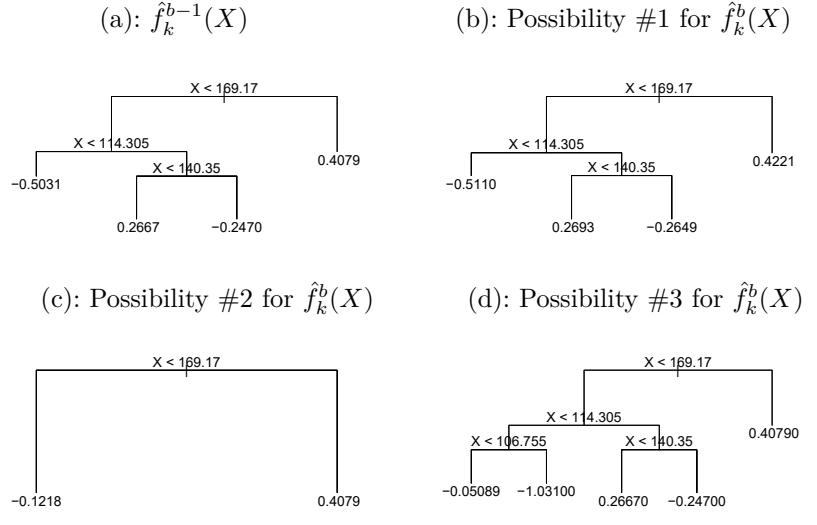
FIGURE 8.12. A schematic of perturbed trees from the BART algorithm. (a): The kth tree at the (b − 1)st iteration, ˆf b−1 k (X), is displayed. Panels (b)–(d) display three of many possibilities for ˆf b k(X), given the form of ˆf b−1 k (X). (b): One possibility is that ˆf b k(X) has the same structure as ˆf b−1 k (X), but with diferent predictions at the terminal nodes. (c): Another possibility is that ˆf b k(X) results from pruning ˆf b−1 k (X). (d): Alternatively, ˆf b k(X) may have more terminal nodes than ˆf b−1 k (X).
values divided by the total number of trees. Thus, ˆf 1(x) = #K k=1 ˆf 1 k (x) = 1 n #n i=1 yi.
In subsequent iterations, BART updates each of the K trees, one at a time. In the bth iteration, to update the kth tree, we subtract from each response value the predictions from all but the kth tree, in order to obtain a partial residual
\[r\_i = y\_i - \sum\_{k'k} \hat{f}\_{k'}^{b-1}(x\_i)\]
for the ith observation, i = 1,…,n. Rather than ftting a fresh tree to this partial residual, BART randomly chooses a perturbation to the tree from the previous iteration ( ˆf b−1 k ) from a set of possible perturbations, favoring ones that improve the ft to the partial residual. There are two components to this perturbation:
- We may change the structure of the tree by adding or pruning branches.
- We may change the prediction in each terminal node of the tree.
Figure 8.12 illustrates examples of possible perturbations to a tree.
The output of BART is a collection of prediction models,
\[\hat{f}^b(x) = \sum\_{k=1}^K \hat{f}\_k^b(x), \text{ for } b = 1, 2, \dots, B.\]
Algorithm 8.3 Bayesian Additive Regression Trees
- Let ˆf 1 1 (x) = ˆf 1 2 (x) = ··· = ˆf 1 K(x) = 1 nK #n i=1 yi.
- Compute ˆf 1(x) = #K k=1 ˆf 1 k (x) = 1 n #n i=1 yi.
- For b = 2,…,B:
- For k = 1, 2,…,K:
- For i = 1,…,n, compute the current partial residual
\[r\_i = y\_i - \sum\_{k'k} \hat{f}\_{k'}^{b-1}(x\_i).\]
- Fit a new tree, ˆf b k(x), to ri, by randomly perturbing the kth tree from the previous iteration, ˆf b−1 k (x). Perturbations that improve the ft are favored.
- Compute ˆf b(x) = #K k=1 ˆf b k(x).
- Compute the mean after L burn-in samples,
\[ \hat{f}(x) = \frac{1}{B - L} \sum\_{b = L + 1}^{B} \hat{f}^b(x). \]
We typically throw away the frst few of these prediction models, since models obtained in the earlier iterations — known as the burn-in period burn-in — tend not to provide very good results. We can let L denote the number of burn-in iterations; for instance, we might take L = 200. Then, to obtain a single prediction, we simply take the average after the burn-in iterations, ˆf(x) = 1 B−L #B b=L+1 ˆf b(x). However, it is also possible to compute quantities other than the average: for instance, the percentiles of ˆfL+1(x),…, ˆf B(x) provide a measure of uncertainty in the fnal prediction. The overall BART procedure is summarized in Algorithm 8.3.
A key element of the BART approach is that in Step 3(a)ii., we do not ft a fresh tree to the current partial residual: instead, we try to improve the ft to the current partial residual by slightly modifying the tree obtained in the previous iteration (see Figure 8.12). Roughly speaking, this guards against overftting since it limits how “hard” we ft the data in each iteration. Furthermore, the individual trees are typically quite small. We limit the tree size in order to avoid overftting the data, which would be more likely to occur if we grew very large trees.
Figure 8.13 shows the result of applying BART to the Heart data, using K = 200 trees, as the number of iterations is increased to 10, 000. During the initial iterations, the test and training errors jump around a bit. After this initial burn-in period, the error rates settle down. We note that there is only a small diference between the training error and the test error, indicating that the tree perturbation process largely avoids overftting.
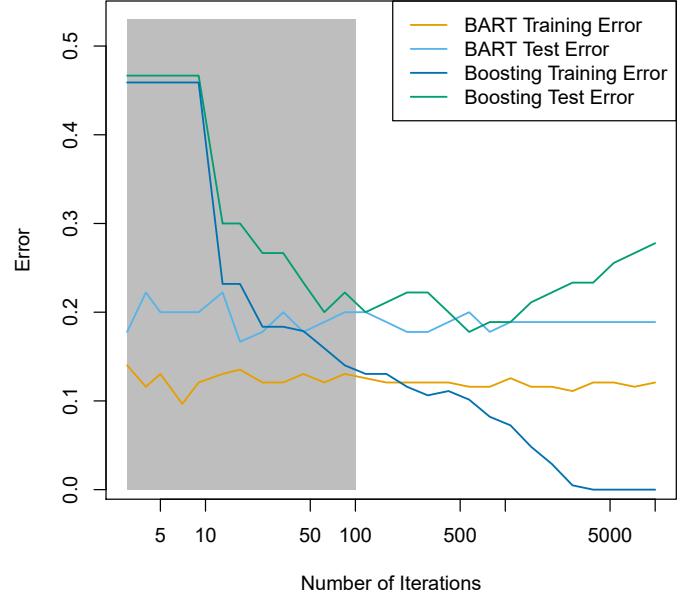
FIGURE 8.13. BART and boosting results for the Heart data. Both training and test errors are displayed. After a burn-in period of 100 iterations (shown in gray), the error rates for BART settle down. Boosting begins to overft after a few hundred iterations.
The training and test errors for boosting are also displayed in Figure 8.13. We see that the test error for boosting approaches that of BART, but then begins to increase as the number of iterations increases. Furthermore, the training error for boosting decreases as the number of iterations increases, indicating that boosting has overft the data.
Though the details are outside of the scope of this book, it turns out that the BART method can be viewed as a Bayesian approach to ftting an ensemble of trees: each time we randomly perturb a tree in order to ft the residuals, we are in fact drawing a new tree from a posterior distribution. (Of course, this Bayesian connection is the motivation for BART’s name.) Furthermore, Algorithm 8.3 can be viewed as a Markov chain Monte Carlo Markov algorithm for ftting the BART model.
chain Monte Carlo
When we apply BART, we must select the number of trees K, the number of iterations B, and the number of burn-in iterations L. We typically choose large values for B and K, and a moderate value for L: for instance, K = 200, B = 1,000, and L = 100 is a reasonable choice. BART has been shown to have very impressive out-of-box performance — that is, it performs well with minimal tuning.
8.2.5 Summary of Tree Ensemble Methods
Trees are an attractive choice of weak learner for an ensemble method for a number of reasons, including their fexibility and ability to handle predictors of mixed types (i.e. qualitative as well as quantitative). We have now seen four approaches for ftting an ensemble of trees: bagging, random forests, boosting, and BART.
- In bagging, the trees are grown independently on random samples of the observations. Consequently, the trees tend to be quite similar to each other. Thus, bagging can get caught in local optima and can fail to thoroughly explore the model space.
- In random forests, the trees are once again grown independently on random samples of the observations. However, each split on each tree is performed using a random subset of the features, thereby decorrelating the trees, and leading to a more thorough exploration of model space relative to bagging.
- In boosting, we only use the original data, and do not draw any random samples. The trees are grown successively, using a “slow” learning approach: each new tree is ft to the signal that is left over from the earlier trees, and shrunken down before it is used.
- In BART, we once again only make use of the original data, and we grow the trees successively. However, each tree is perturbed in order to avoid local minima and achieve a more thorough exploration of the model space.
8.3 Lab: Tree-Based Methods
We import some of our usual libraries at this top level.
In [1]: import numpy as np
import pandas as pd
from matplotlib.pyplot import subplots
from statsmodels.datasets import get_rdataset
import sklearn.model_selection as skm
from ISLP import load_data, confusion_table
from ISLP.models import ModelSpec as MSWe also collect the new imports needed for this lab.
In [2]: from sklearn.tree import (DecisionTreeClassifier as DTC,
DecisionTreeRegressor as DTR,
plot_tree,
export_text)
from sklearn.metrics import (accuracy_score,
log_loss)
from sklearn.ensemble import \
(RandomForestRegressor as RF,
GradientBoostingRegressor as GBR)
from ISLP.bart import BART8.3.1 Fitting Classifcation Trees
We frst use classifcation trees to analyze the Carseats data set. In these data, Sales is a continuous variable, and so we begin by recoding it as a binary variable. We use the where() function to create a variable, called where() High, which takes on a value of Yes if the Sales variable exceeds 8, and takes on a value of No otherwise.
In [3]: Carseats = load_data('Carseats')
High = np.where(Carseats.Sales > 8,
"Yes",
"No")We now use DecisionTreeClassifier() to ft a classifcation tree in order DecisionTree Classifier() to predict High using all variables but Sales. To do so, we must form a model matrix as we did when ftting regression models.
In [4]: model = MS(Carseats.columns.drop('Sales'), intercept=False)
D = model.fit_transform(Carseats)
feature_names = list(D.columns)
X = np.asarray(D)We have converted D from a data frame to an array X, which is needed in some of the analysis below. We also need the feature_names for annotating our plots later.
There are several options needed to specify the classifer, such as max_depth (how deep to grow the tree), min_samples_split (minimum number of observations in a node to be eligible for splitting) and criterion (whether to use Gini or cross-entropy as the split criterion). We also set random_state for reproducibility; ties in the split criterion are broken at random.
In [5]: clf = DTC(criterion='entropy',
max_depth=3,
random_state=0)
clf.fit(X, High)Out[5]: DecisionTreeClassifier(criterion=‘entropy’, max_depth=3)
In our discussion of qualitative features in Section 3.3, we noted that for a linear regression model such a feature could be represented by including a matrix of dummy variables (one-hot-encoding) in the model matrix, using the formula notation of statsmodels. As mentioned in Section 8.1, there is a more natural way to handle qualitative features when building a decision tree, that does not require such dummy variables; each split amounts to partitioning the levels into two groups. However, the sklearn implementation of decision trees does not take advantage of this approach; instead it simply treats the one-hot-encoded levels as separate variables.
In [6]: accuracy_score(High, clf.predict(X))Out[6]: 0.7275
With only the default arguments, the training error rate is 21%. For classifcation trees, we can access the value of the deviance using log_loss(), log_loss()
356 8. Tree-Based Methods
\[-2\sum\_{m}\sum\_{k} n\_{mk}\log\hat{p}\_{mk},\]
where nmk is the number of observations in the mth terminal node that belong to the kth class.
In [7]: resid_dev = np.sum(log_loss(High, clf.predict_proba(X)))
resid_devOut[7]: 0.4711
This is closely related to the entropy, defned in (8.7). A small deviance indicates a tree that provides a good ft to the (training) data.
One of the most attractive properties of trees is that they can be graphically displayed. Here we use the plot() function to display the tree structure (not shown here).
In [8]: ax = subplots(figsize=(12,12))[1]
plot_tree(clf,
feature_names=feature_names,
ax=ax);The most important indicator of Sales appears to be ShelveLoc.
We can see a text representation of the tree using export_text(), which export_text() displays the split criterion (e.g. Price <= 92.5) for each branch. For leaf nodes it shows the overall prediction (Yes or No). We can also see the number of observations in that leaf that take on values of Yes and No by specifying show_weights=True.
In [9]: print(export_text(clf,
feature_names=feature_names,
show_weights=True))Out[9]: |--- ShelveLoc[Good] <= 0.50
| |--- Price <= 92.50
| | |--- Income <= 57.00
| | | |--- weights: [7.00, 3.00] class: No
| | |--- Income > 57.00
| | | |--- weights: [7.00, 29.00] class: Yes
| |--- Price > 92.50
| | |--- Advertising <= 13.50
| | | |--- weights: [183.00, 41.00] class: No
| | |--- Advertising > 13.50
| | | |--- weights: [20.00, 25.00] class: Yes
|--- ShelveLoc[Good] > 0.50
| |--- Price <= 135.00
| | |--- US[Yes] <= 0.50
| | | |--- weights: [6.00, 11.00] class: Yes
| | |--- US[Yes] > 0.50
| | | |--- weights: [2.00, 49.00] class: Yes
| |--- Price > 135.00
| | |--- Income <= 46.00
| | | |--- weights: [6.00, 0.00] class: No
| | |--- Income > 46.00
| | | |--- weights: [5.00, 6.00] class: YesIn order to properly evaluate the performance of a classifcation tree on these data, we must estimate the test error rather than simply computing the training error. We split the observations into a training set and a test set, build the tree using the training set, and evaluate its performance on the test data. This pattern is similar to that in Chapter 6, with the linear models replaced here by decision trees — the code for validation is almost identical. This approach leads to correct predictions for 68.5% of the locations in the test data set.
In [10]: validation = skm.ShuffleSplit(n_splits=1,
test_size=200,
random_state=0)
results = skm.cross_validate(clf,
D,
High,
cv=validation)
results['test_score']Out[10]: array([0.685])
Next, we consider whether pruning the tree might lead to improved classifcation performance. We frst split the data into a training and test set. We will use cross-validation to prune the tree on the training set, and then evaluate the performance of the pruned tree on the test set.
In [11]: (X_train,
X_test,
High_train,
High_test) = skm.train_test_split(X,
High,
test_size=0.5,
random_state=0)We frst reft the full tree on the training set; here we do not set a max_depth parameter, since we will learn that through cross-validation.
In [12]: clf = DTC(criterion='entropy', random_state=0)
clf.fit(X_train, High_train)
accuracy_score(High_test, clf.predict(X_test))Out[12]: 0.735
Next we use the cost_complexity_pruning_path() method of clf to extract cost_ cost-complexity values.
complexity_pruning_
path()In [13]: ccp_path = clf.cost_complexity_pruning_path(X_train, High_train)
kfold = skm.KFold(10,
random_state=1,
shuffle=True)This yields a set of impurities and α values from which we can extract an optimal one by cross-validation.
In [14]: grid = skm.GridSearchCV(clf,
{'ccp_alpha': ccp_path.ccp_alphas},
refit=True,358 8. Tree-Based Methods
cv=kfold,
scoring='accuracy')
grid.fit(X_train, High_train)
grid.best_score_Out[14]: 0.685
Let’s take a look at the pruned true.
In [15]: ax = subplots(figsize=(12, 12))[1]
best_ = grid.best_estimator_
plot_tree(best_,
feature_names=feature_names,
ax=ax);
# print the split criterion for the prunded tree
print(export_text(best_,
feature_names=feature_names,
show_weights=True))This is quite a bushy tree. We could count the leaves, or query best_ instead.
In [16]: best_.tree_.n_leavesOut[16]: 30
The tree with 30 terminal nodes results in the lowest cross-validation error rate, with an accuracy of 68.5%. How well does this pruned tree perform on the test data set? Once again, we apply the predict() function.
In [17]: print(accuracy_score(High_test,
best_.predict(X_test)))
confusion = confusion_table(best_.predict(X_test),
High_test)
confusionOut[17]: 0.72
Truth No Yes Predicted No 108 61 Yes 10 21
Now 72.0% of the test observations are correctly classifed, which is slightly worse than the error for the full tree (with 35 leaves). So crossvalidation has not helped us much here; it only pruned of 5 leaves, at a cost of a slightly worse error. These results would change if we were to change the random number seeds above; even though cross-validation gives an unbiased approach to model selection, it does have variance.
8.3.2 Fitting Regression Trees
Here we ft a regression tree to the Boston data set. The steps are similar to those for classifcation trees.
In [18]: Boston = load_data("Boston")
model = MS(Boston.columns.drop('medv'), intercept=False)
D = model.fit_transform(Boston)
feature_names = list(D.columns)
X = np.asarray(D)First, we split the data into training and test sets, and ft the tree to the training data. Here we use 30% of the data for the test set.
In [19]: (X_train,
X_test,
y_train,
y_test) = skm.train_test_split(X,
Boston['medv'],
test_size=0.3,
random_state=0)Having formed our training and test data sets, we ft the regression tree.
In [20]: reg = DTR(max_depth=3)
reg.fit(X_train, y_train)
ax = subplots(figsize=(12,12))[1]
plot_tree(reg,
feature_names=feature_names,
ax=ax);The variable lstat measures the percentage of individuals with lower socioeconomic status. The tree indicates that lower values of lstat correspond to more expensive houses. The tree predicts a median house price of $12,042 for small-sized homes (rm < 6.8), in suburbs in which residents have low socioeconomic status (lstat > 14.4) and the crime-rate is moderate (crim > 5.8).
Now we use the cross-validation function to see whether pruning the tree will improve performance.
In [21]: ccp_path = reg.cost_complexity_pruning_path(X_train, y_train)
kfold = skm.KFold(5,shuffle=True,
random_state=10)
grid = skm.GridSearchCV(reg,
{'ccp_alpha': ccp_path.ccp_alphas},
refit=True,
cv=kfold,
scoring='neg_mean_squared_error')
G = grid.fit(X_train, y_train)In keeping with the cross-validation results, we use the pruned tree to make predictions on the test set.
In [22]: best_ = grid.best_estimator_
np.mean((y_test - best_.predict(X_test))**2)Out[22]: 28.07
In other words, the test set MSE associated with the regression tree is 28.07. The square root of the MSE is therefore around 5.30, indicating that this model leads to test predictions that are within around $5300 of the true median home value for the suburb.
Let’s plot the best tree to see how interpretable it is.
In [23]: ax = subplots(figsize=(12,12))[1]
plot_tree(G.best_estimator_,
feature_names=feature_names,
ax=ax);360 8. Tree-Based Methods
8.3.3 Bagging and Random Forests
Here we apply bagging and random forests to the Boston data, using the RandomForestRegressor() from the sklearn.ensemble package. Recall that RandomForest bagging is simply a special case of a random forest with m = p. Therefore, the RandomForestRegressor() function can be used to perform both bagging and random forests. We start with bagging.
Regressor() sklearn. ensemble
In [24]: bag_boston = RF(max_features=X_train.shape[1], random_state=0)
bag_boston.fit(X_train, y_train)Out[24]: RandomForestRegressor(max_features=12, random_state=0)
The argument max_features indicates that all 12 predictors should be considered for each split of the tree — in other words, that bagging should be done. How well does this bagged model perform on the test set?
In [25]: ax = subplots(figsize=(8,8))[1]
y_hat_bag = bag_boston.predict(X_test)
ax.scatter(y_hat_bag, y_test)
np.mean((y_test - y_hat_bag)**2)Out[25]: 14.63
The test set MSE associated with the bagged regression tree is 14.63, about half that obtained using an optimally-pruned single tree. We could change the number of trees grown from the default of 100 by using the n_estimators argument:
In [26]: bag_boston = RF(max_features=X_train.shape[1],
n_estimators=500,
random_state=0).fit(X_train, y_train)
y_hat_bag = bag_boston.predict(X_test)
np.mean((y_test - y_hat_bag)**2)Out[26]: 14.61
There is not much change. Bagging and random forests cannot overft by increasing the number of trees, but can underft if the number is too small.
Growing a random forest proceeds in exactly the same way, except that we use a smaller value of the max_features argument. By default, RandomForestRegressor() uses p variables when building a random forest of regression trees (i.e. it defaults to bagging), and RandomForestClassifier() uses √p variables when building a random forest of classifcation trees. Here we use max_features=6.
In [27]: RF_boston = RF(max_features=6,
random_state=0).fit(X_train, y_train)
y_hat_RF = RF_boston.predict(X_test)
np.mean((y_test - y_hat_RF)**2)Out[27]: 20.04
The test set MSE is 20.04; this indicates that random forests did somewhat worse than bagging in this case. Extracting the feature_importances_ values from the ftted model, we can view the importance of each variable.
In [28]: feature_imp = pd.DataFrame(
{'importance':RF_boston.feature_importances_},
index=feature_names)
feature_imp.sort_values(by='importance', ascending=False)Out[28]: importance
| lstat | 0.368683 |
|---|---|
| rm | 0.333842 |
| ptratio | 0.057306 |
| indus | 0.053303 |
| crim | 0.052426 |
| dis | 0.042493 |
| nox | 0.034410 |
| age | 0.024327 |
| tax | 0.022368 |
| rad | 0.005048 |
| zn | 0.003238 |
| chas | 0.002557 |
This is a relative measure of the total decrease in node impurity that results from splits over that variable, averaged over all trees (this was plotted in Figure 8.9 for a model ft to the Heart data).
The results indicate that across all of the trees considered in the random forest, the wealth level of the community (lstat) and the house size (rm) are by far the two most important variables.
8.3.4 Boosting
Here we use GradientBoostingRegressor() from sklearn.ensemble to ft Gradient boosted regression trees to the Boston data set. For classifcation we would use GradientBoostingClassifier(). The argument n_estimators=5000 indicates that we want 5000 trees, and the option max_depth=3 limits the depth of each tree. The argument learning_rate is the λ mentioned earlier in the description of boosting.
Boosting Regressor() Gradient Boosting Classifier()
In [29]: boost_boston = GBR(n_estimators=5000,
learning_rate=0.001,
max_depth=3,
random_state=0)
boost_boston.fit(X_train, y_train)We can see how the training error decreases with the train_score_ attribute. To get an idea of how the test error decreases we can use the staged_predict() method to get the predicted values along the path.
In [30]: test_error = np.zeros_like(boost_boston.train_score_)for idx, y_ in enumerate(boost_boston.staged_predict(X_test)):
test_error[idx] = np.mean((y_test - y_)**2)
plot_idx = np.arange(boost_boston.train_score_.shape[0])
ax = subplots(figsize=(8,8))[1]
ax.plot(plot_idx,
boost_boston.train_score_,
'b',
label='Training')362 8. Tree-Based Methods
ax.plot(plot_idx,
test_error,
'r',
label='Test')
ax.legend();We now use the boosted model to predict medv on the test set:
In [31]: y_hat_boost = boost_boston.predict(X_test);
np.mean((y_test - y_hat_boost)**2)Out[31]: 14.48
The test MSE obtained is 14.48, similar to the test MSE for bagging. If we want to, we can perform boosting with a diferent value of the shrinkage parameter λ in (8.10). The default value is 0.001, but this is easily modifed. Here we take λ = 0.2.
In [32]: boost_boston = GBR(n_estimators=5000,
learning_rate=0.2,
max_depth=3,
random_state=0)
boost_boston.fit(X_train,
y_train)
y_hat_boost = boost_boston.predict(X_test);
np.mean((y_test - y_hat_boost)**2)Out[32]: 14.50
In this case, using λ = 0.2 leads to a almost the same test MSE as when using λ = 0.001.
8.3.5 Bayesian Additive Regression Trees
In this section we demonstrate a Python implementation of BART found in the ISLP.bart package. We ft a model to the Boston housing data set. This BART() estimator is designed for quantitative outcome variables, though BART() other implementations are available for ftting logistic and probit models to categorical outcomes.
In [33]: bart_boston = BART(random_state=0, burnin=5, ndraw=15)
bart_boston.fit(X_train, y_train)Out[33]: BART(burnin=5, ndraw=15, random_state=0)
On this data set, with this split into test and training, we see that the test error of BART is similar to that of random forest.
In [34]: yhat_test = bart_boston.predict(X_test.astype(np.float32))
np.mean((y_test - yhat_test)**2)Out[34]: 20.92
We can check how many times each variable appeared in the collection of trees. This gives a summary similar to the variable importance plot for boosting and random forests.
In [35]: var_inclusion = pd.Series(bart_boston.variable_inclusion_.mean(0),
index=D.columns)
var_inclusion
Out[35]: crim 25.333333
zn 27.000000
indus 21.266667
chas 20.466667
nox 25.400000
rm 32.400000
age 26.133333
dis 25.666667
rad 24.666667
tax 23.933333
ptratio 25.000000
lstat 31.866667
dtype: float648.4 Exercises
Conceptual
- Draw an example (of your own invention) of a partition of twodimensional feature space that could result from recursive binary splitting. Your example should contain at least six regions. Draw a decision tree corresponding to this partition. Be sure to label all aspects of your fgures, including the regions R1, R2,…, the cutpoints t1, t2,…, and so forth.
Hint: Your result should look something like Figures 8.1 and 8.2.
- It is mentioned in Section 8.2.3 that boosting using depth-one trees (or stumps) leads to an additive model: that is, a model of the form
\[f(X) = \sum\_{j=1}^{p} f\_j(X\_j).\]
Explain why this is the case. You can begin with (8.12) in Algorithm 8.2.
- Consider the Gini index, classifcation error, and entropy in a simple classifcation setting with two classes. Create a single plot that displays each of these quantities as a function of pˆm1. The x-axis should display pˆm1, ranging from 0 to 1, and the y-axis should display the value of the Gini index, classifcation error, and entropy.
Hint: In a setting with two classes, pˆm1 = 1 − pˆm2. You could make this plot by hand, but it will be much easier to make in R.
- This question relates to the plots in Figure 8.14.
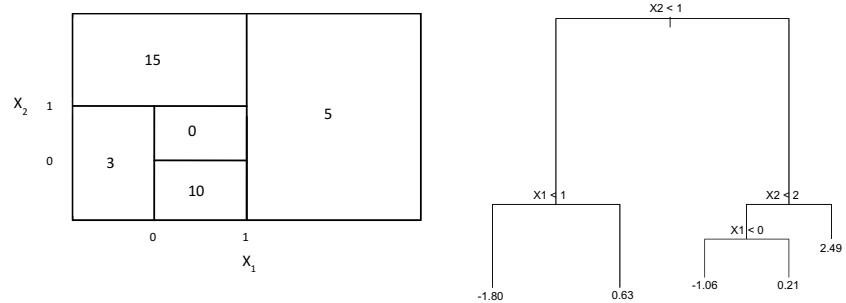
FIGURE 8.14. Left: A partition of the predictor space corresponding to Exercise 4a. Right: A tree corresponding to Exercise 4b.
- Sketch the tree corresponding to the partition of the predictor space illustrated in the left-hand panel of Figure 8.14. The numbers inside the boxes indicate the mean of Y within each region.
- Create a diagram similar to the left-hand panel of Figure 8.14, using the tree illustrated in the right-hand panel of the same fgure. You should divide up the predictor space into the correct regions, and indicate the mean for each region.
- Suppose we produce ten bootstrapped samples from a data set containing red and green classes. We then apply a classifcation tree to each bootstrapped sample and, for a specifc value of X, produce 10 estimates of P(Class is Red|X):
0.1, 0.15, 0.2, 0.2, 0.55, 0.6, 0.6, 0.65, 0.7, and 0.75.
There are two common ways to combine these results together into a single class prediction. One is the majority vote approach discussed in this chapter. The second approach is to classify based on the average probability. In this example, what is the fnal classifcation under each of these two approaches?
- Provide a detailed explanation of the algorithm that is used to ft a regression tree.
Applied
- In Section 8.3.3, we applied random forests to the Boston data using max_features = 6 and using n_estimators = 100 and n_estimators = 500. Create a plot displaying the test error resulting from random forests on this data set for a more comprehensive range of values for max_features and n_estimators. You can model your plot after Figure 8.10. Describe the results obtained.
- In the lab, a classifcation tree was applied to the Carseats data set after converting Sales into a qualitative response variable. Now we will seek to predict Sales using regression trees and related approaches, treating the response as a quantitative variable.
- Split the data set into a training set and a test set.
- Fit a regression tree to the training set. Plot the tree, and interpret the results. What test MSE do you obtain?
- Use cross-validation in order to determine the optimal level of tree complexity. Does pruning the tree improve the test MSE?
- Use the bagging approach in order to analyze this data. What test MSE do you obtain? Use the feature_importance_ values to determine which variables are most important.
- Use random forests to analyze this data. What test MSE do you obtain? Use the feature_importance_ values to determine which variables are most important. Describe the efect of m, the number of variables considered at each split, on the error rate obtained.
- Now analyze the data using BART, and report your results.
- This problem involves the OJ data set which is part of the ISLP package.
- Create a training set containing a random sample of 800 observations, and a test set containing the remaining observations.
- Fit a tree to the training data, with Purchase as the response and the other variables as predictors. What is the training error rate?
- Create a plot of the tree, and interpret the results. How many terminal nodes does the tree have?
- Use the export_tree() function to produce a text summary of the ftted tree. Pick one of the terminal nodes, and interpret the information displayed.
- Predict the response on the test data, and produce a confusion matrix comparing the test labels to the predicted test labels. What is the test error rate?
- Use cross-validation on the training set in order to determine the optimal tree size.
- Produce a plot with tree size on the x-axis and cross-validated classifcation error rate on the y-axis.
- Which tree size corresponds to the lowest cross-validated classifcation error rate?
- Produce a pruned tree corresponding to the optimal tree size obtained using cross-validation. If cross-validation does not lead to selection of a pruned tree, then create a pruned tree with fve terminal nodes.
- Compare the training error rates between the pruned and unpruned trees. Which is higher?
- Compare the test error rates between the pruned and unpruned trees. Which is higher?
- We now use boosting to predict Salary in the Hitters data set.
- Remove the observations for whom the salary information is unknown, and then log-transform the salaries.
- Create a training set consisting of the frst 200 observations, and a test set consisting of the remaining observations.
- Perform boosting on the training set with 1,000 trees for a range of values of the shrinkage parameter λ. Produce a plot with diferent shrinkage values on the x-axis and the corresponding training set MSE on the y-axis.
- Produce a plot with diferent shrinkage values on the x-axis and the corresponding test set MSE on the y-axis.
- Which variables appear to be the most important predictors in the boosted model?
- Now apply bagging to the training set. What is the test set MSE for this approach?
- This question uses the Caravan data set.
- Create a training set consisting of the frst 1,000 observations, and a test set consisting of the remaining observations.
- Fit a boosting model to the training set with Purchase as the response and the other variables as predictors. Use 1,000 trees, and a shrinkage value of 0.01. Which predictors appear to be the most important?
- Use the boosting model to predict the response on the test data. Predict that a person will make a purchase if the estimated probability of purchase is greater than 20 %. Form a confusion matrix. What fraction of the people predicted to make a purchase do in fact make one? How does this compare with the results obtained from applying KNN or logistic regression to this data set?
- Apply boosting, bagging, random forests, and BART to a data set of your choice. Be sure to ft the models on a training set and to evaluate their performance on a test set. How accurate are the results compared to simple methods like linear or logistic regression? Which of these approaches yields the best performance?
9 Support Vector Machines

In this chapter, we discuss the support vector machine (SVM), an approach for classifcation that was developed in the computer science community in the 1990s and that has grown in popularity since then. SVMs have been shown to perform well in a variety of settings, and are often considered one of the best “out of the box” classifers.
The support vector machine is a generalization of a simple and intuitive classifer called the maximal margin classifer, which we introduce in Section 9.1. Though it is elegant and simple, we will see that this classifer unfortunately cannot be applied to most data sets, since it requires that the classes be separable by a linear boundary. In Section 9.2, we introduce the support vector classifer, an extension of the maximal margin classifer that can be applied in a broader range of cases. Section 9.3 introduces the support vector machine, which is a further extension of the support vector classifer in order to accommodate non-linear class boundaries. Support vector machines are intended for the binary classifcation setting in which there are two classes; in Section 9.4 we discuss extensions of support vector machines to the case of more than two classes. In Section 9.5 we discuss the close connections between support vector machines and other statistical methods such as logistic regression.
People often loosely refer to the maximal margin classifer, the support vector classifer, and the support vector machine as “support vector machines”. To avoid confusion, we will carefully distinguish between these three notions in this chapter.
9.1 Maximal Margin Classifer
In this section, we defne a hyperplane and introduce the concept of an optimal separating hyperplane.
© Springer Nature Switzerland AG 2023
G. James et al., An Introduction to Statistical Learning, Springer Texts in Statistics, https://doi.org/10.1007/978-3-031-38747-0\_9
368 9. Support Vector Machines
9.1.1 What Is a Hyperplane?
In a p-dimensional space, a hyperplane is a fat afne subspace of hyperplane dimension p − 1. 1 For instance, in two dimensions, a hyperplane is a fat one-dimensional subspace—in other words, a line. In three dimensions, a hyperplane is a fat two-dimensional subspace—that is, a plane. In p > 3 dimensions, it can be hard to visualize a hyperplane, but the notion of a (p − 1)-dimensional fat subspace still applies.
The mathematical defnition of a hyperplane is quite simple. In two dimensions, a hyperplane is defned by the equation
\[ \beta\_0 + \beta\_1 X\_1 + \beta\_2 X\_2 = 0 \tag{9.1} \]
for parameters β0, β1, and β2. When we say that (9.1) “defnes” the hyperplane, we mean that any X = (X1, X2)T for which (9.1) holds is a point on the hyperplane. Note that (9.1) is simply the equation of a line, since indeed in two dimensions a hyperplane is a line.
Equation 9.1 can be easily extended to the p-dimensional setting:
\[ \beta\_0 + \beta\_1 X\_1 + \beta\_2 X\_2 + \dots + \beta\_p X\_p = 0 \tag{9.2} \]
defnes a p-dimensional hyperplane, again in the sense that if a point X = (X1, X2,…,Xp)T in p-dimensional space (i.e. a vector of length p) satisfes (9.2), then X lies on the hyperplane.
Now, suppose that X does not satisfy (9.2); rather,
\[ \beta\_0 + \beta\_1 X\_1 + \beta\_2 X\_2 + \dots + \beta\_p X\_p > 0. \tag{9.3} \]
Then this tells us that X lies to one side of the hyperplane. On the other hand, if
\[ \beta\_0 + \beta\_1 X\_1 + \beta\_2 X\_2 + \dots + \beta\_p X\_p < 0,\tag{9.4} \]
then X lies on the other side of the hyperplane. So we can think of the hyperplane as dividing p-dimensional space into two halves. One can easily determine on which side of the hyperplane a point lies by simply calculating the sign of the left-hand side of (9.2). A hyperplane in two-dimensional space is shown in Figure 9.1.
9.1.2 Classifcation Using a Separating Hyperplane
Now suppose that we have an n × p data matrix X that consists of n training observations in p-dimensional space,
\[x\_1 = \begin{pmatrix} x\_{11} \\ \vdots \\ x\_{1p} \end{pmatrix}, \dots, x\_n = \begin{pmatrix} x\_{n1} \\ \vdots \\ x\_{np} \end{pmatrix}, \tag{9.5}\]
and that these observations fall into two classes—that is, y1,…,yn ∈ {−1, 1} where −1 represents one class and 1 the other class. We also have a
1The word afne indicates that the subspace need not pass through the origin.
FIGURE 9.1. The hyperplane 1+2X1 + 3X2 = 0 is shown. The blue region is the set of points for which 1+2X1 + 3X2 > 0, and the purple region is the set of points for which 1+2X1 + 3X2 < 0.
test observation, a p-vector of observed features x∗ = 5 x∗ 1 … x∗ p 6T . Our goal is to develop a classifer based on the training data that will correctly classify the test observation using its feature measurements. We have seen a number of approaches for this task, such as linear discriminant analysis and logistic regression in Chapter 4, and classifcation trees, bagging, and boosting in Chapter 8. We will now see a new approach that is based upon the concept of a separating hyperplane. separating
hyperplane Suppose that it is possible to construct a hyperplane that separates the training observations perfectly according to their class labels. Examples of three such separating hyperplanes are shown in the left-hand panel of Figure 9.2. We can label the observations from the blue class as yi = 1 and those from the purple class as yi = −1. Then a separating hyperplane has the property that
\[ \beta\_0 + \beta\_1 x\_{i1} + \beta\_2 x\_{i2} + \dots + \beta\_p x\_{ip} > 0 \text{ if } y\_i = 1,\tag{9.6} \]
and
β0 + β1xi1 + β2xi2 + ··· + βpxip < 0 if yi = −1. (9.7)
Equivalently, a separating hyperplane has the property that
\[y\_i(\beta\_0 + \beta\_1 x\_{i1} + \beta\_2 x\_{i2} + \dots + \beta\_p x\_{ip}) > 0\tag{9.8}\]
for all i = 1,…,n.
If a separating hyperplane exists, we can use it to construct a very natural classifer: a test observation is assigned a class depending on which side of the hyperplane it is located. The right-hand panel of Figure 9.2 shows an example of such a classifer. That is, we classify the test observation x∗ based on the sign of f(x∗) = β0+β1x∗ 1+β2x∗ 2+···+βpx∗ p. If f(x∗) is positive, then we assign the test observation to class 1, and if f(x∗) is negative, then we assign it to class −1. We can also make use of the magnitude of f(x∗). If
FIGURE 9.2. Left: There are two classes of observations, shown in blue and in purple, each of which has measurements on two variables. Three separating hyperplanes, out of many possible, are shown in black. Right: A separating hyperplane is shown in black. The blue and purple grid indicates the decision rule made by a classifer based on this separating hyperplane: a test observation that falls in the blue portion of the grid will be assigned to the blue class, and a test observation that falls into the purple portion of the grid will be assigned to the purple class.
f(x∗) is far from zero, then this means that x∗ lies far from the hyperplane, and so we can be confdent about our class assignment for x∗. On the other hand, if f(x∗) is close to zero, then x∗ is located near the hyperplane, and so we are less certain about the class assignment for x∗. Not surprisingly, and as we see in Figure 9.2, a classifer that is based on a separating hyperplane leads to a linear decision boundary.
9.1.3 The Maximal Margin Classifer
In general, if our data can be perfectly separated using a hyperplane, then there will in fact exist an infnite number of such hyperplanes. This is because a given separating hyperplane can usually be shifted a tiny bit up or down, or rotated, without coming into contact with any of the observations. Three possible separating hyperplanes are shown in the left-hand panel of Figure 9.2. In order to construct a classifer based upon a separating hyperplane, we must have a reasonable way to decide which of the infnite possible separating hyperplanes to use.
A natural choice is the maximal margin hyperplane (also known as the maximal optimal separating hyperplane), which is the separating hyperplane that is farthest from the training observations. That is, we can compute the (perpendicular) distance from each training observation to a given separating hyperplane; the smallest such distance is the minimal distance from the observations to the hyperplane, and is known as the margin. The maximal margin hyperplane is the separating hyperplane for which the margin is margin largest—that is, it is the hyperplane that has the farthest minimum distance to the training observations. We can then classify a test observation based on which side of the maximal margin hyperplane it lies. This is known
margin hyperplane optimal separating hyperplane
FIGURE 9.3. There are two classes of observations, shown in blue and in purple. The maximal margin hyperplane is shown as a solid line. The margin is the distance from the solid line to either of the dashed lines. The two blue points and the purple point that lie on the dashed lines are the support vectors, and the distance from those points to the hyperplane is indicated by arrows. The purple and blue grid indicates the decision rule made by a classifer based on this separating hyperplane.
as the maximal margin classifer. We hope that a classifer that has a large maximal margin on the training data will also have a large margin on the test data, and hence will classify the test observations correctly. Although the maximal margin classifer is often successful, it can also lead to overftting when p is large.
margin classifer
If β0, β1,…, βp are the coefcients of the maximal margin hyperplane, then the maximal margin classifer classifes the test observation x∗ based on the sign of f(x∗) = β0 + β1x∗ 1 + β2x∗ 2 + ··· + βpx∗ p.
Figure 9.3 shows the maximal margin hyperplane on the data set of Figure 9.2. Comparing the right-hand panel of Figure 9.2 to Figure 9.3, we see that the maximal margin hyperplane shown in Figure 9.3 does indeed result in a greater minimal distance between the observations and the separating hyperplane—that is, a larger margin. In a sense, the maximal margin hyperplane represents the mid-line of the widest “slab” that we can insert between the two classes.
Examining Figure 9.3, we see that three training observations are equidistant from the maximal margin hyperplane and lie along the dashed lines indicating the width of the margin. These three observations are known as support vectors, since they are vectors in p-dimensional space (in Figure 9.3, support vector p = 2) and they “support” the maximal margin hyperplane in the sense that if these points were moved slightly then the maximal margin hyperplane would move as well. Interestingly, the maximal margin hyperplane depends directly on the support vectors, but not on the other observations: a movement to any of the other observations would not afect the separating hyperplane, provided that the observation’s movement does not cause it to
cross the boundary set by the margin. The fact that the maximal margin hyperplane depends directly on only a small subset of the observations is an important property that will arise later in this chapter when we discuss the support vector classifer and support vector machines.
9.1.4 Construction of the Maximal Margin Classifer
We now consider the task of constructing the maximal margin hyperplane based on a set of n training observations x1,…,xn ∈ Rp and associated class labels y1,…,yn ∈ {−1, 1}. Briefy, the maximal margin hyperplane is the solution to the optimization problem
\[\underset{\beta\_0, \beta\_1, \dots, \beta\_p, M}{\text{maximize }} M \tag{9.9}\]
\[\text{subject to } \sum\_{j=1}^{p} \beta\_j^2 = 1,\tag{9.10}\]
\[y\_i(\beta\_0 + \beta\_1 x\_{i1} + \beta\_2 x\_{i2} + \dots + \beta\_p x\_{ip}) \ge M \; \forall \; i = 1, \dots, n. \; (9.11)\]
This optimization problem (9.9)–(9.11) is actually simpler than it looks. First of all, the constraint in (9.11) that
\[y\_i(\beta\_0 + \beta\_1 x\_{i1} + \beta\_2 x\_{i2} + \dots + \beta\_p x\_{ip}) \ge M \quad \forall \ i = 1, \dots, n\]
guarantees that each observation will be on the correct side of the hyperplane, provided that M is positive. (Actually, for each observation to be on the correct side of the hyperplane we would simply need yi(β0 +β1xi1 + β2xi2+···+βpxip) > 0, so the constraint in (9.11) in fact requires that each observation be on the correct side of the hyperplane, with some cushion, provided that M is positive.)
Second, note that (9.10) is not really a constraint on the hyperplane, since if β0 + β1xi1 + β2xi2 + ··· + βpxip = 0 defnes a hyperplane, then so does k(β0 +β1xi1 +β2xi2 +···+βpxip)=0 for any k = 0 ̸ . However, (9.10) adds meaning to (9.11); one can show that with this constraint the perpendicular distance from the ith observation to the hyperplane is given by
\[y\_i(\beta\_0 + \beta\_1 x\_{i1} + \beta\_2 x\_{i2} + \dots + \beta\_p x\_{ip}).\]
Therefore, the constraints (9.10) and (9.11) ensure that each observation is on the correct side of the hyperplane and at least a distance M from the hyperplane. Hence, M represents the margin of our hyperplane, and the optimization problem chooses β0, β1,…, βp to maximize M. This is exactly the defnition of the maximal margin hyperplane! The problem (9.9)–(9.11) can be solved efciently, but details of this optimization are outside of the scope of this book.
9.1.5 The Non-separable Case
The maximal margin classifer is a very natural way to perform classifcation, if a separating hyperplane exists. However, as we have hinted, in many cases no separating hyperplane exists, and so there is no maximal
FIGURE 9.4. There are two classes of observations, shown in blue and in purple. In this case, the two classes are not separable by a hyperplane, and so the maximal margin classifer cannot be used.
margin classifer. In this case, the optimization problem (9.9)–(9.11) has no solution with M > 0. An example is shown in Figure 9.4. In this case, we cannot exactly separate the two classes. However, as we will see in the next section, we can extend the concept of a separating hyperplane in order to develop a hyperplane that almost separates the classes, using a so-called soft margin. The generalization of the maximal margin classifer to the non-separable case is known as the support vector classifer.
9.2 Support Vector Classifers
9.2.1 Overview of the Support Vector Classifer
In Figure 9.4, we see that observations that belong to two classes are not necessarily separable by a hyperplane. In fact, even if a separating hyperplane does exist, then there are instances in which a classifer based on a separating hyperplane might not be desirable. A classifer based on a separating hyperplane will necessarily perfectly classify all of the training observations; this can lead to sensitivity to individual observations. An example is shown in Figure 9.5. The addition of a single observation in the right-hand panel of Figure 9.5 leads to a dramatic change in the maximal margin hyperplane. The resulting maximal margin hyperplane is not satisfactory—for one thing, it has only a tiny margin. This is problematic because as discussed previously, the distance of an observation from the hyperplane can be seen as a measure of our confdence that the observation was correctly classifed. Moreover, the fact that the maximal margin hyperplane is extremely sensitive to a change in a single observation suggests that it may have overft the training data.
In this case, we might be willing to consider a classifer based on a hyperplane that does not perfectly separate the two classes, in the interest of
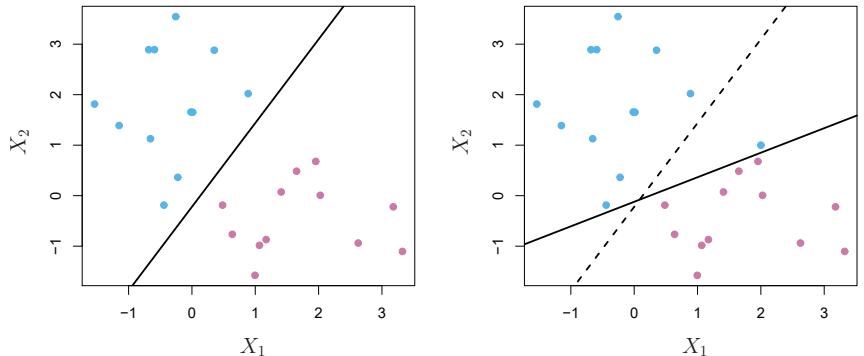
FIGURE 9.5. Left: Two classes of observations are shown in blue and in purple, along with the maximal margin hyperplane. Right: An additional blue observation has been added, leading to a dramatic shift in the maximal margin hyperplane shown as a solid line. The dashed line indicates the maximal margin hyperplane that was obtained in the absence of this additional point.
- Greater robustness to individual observations, and
- Better classifcation of most of the training observations.
That is, it could be worthwhile to misclassify a few training observations in order to do a better job in classifying the remaining observations.
The support vector classifer, sometimes called a soft margin classifer, support does exactly this. Rather than seeking the largest possible margin so that every observation is not only on the correct side of the hyperplane but also on the correct side of the margin, we instead allow some observations to be on the incorrect side of the margin, or even the incorrect side of the hyperplane. (The margin is soft because it can be violated by some of the training observations.) An example is shown in the left-hand panel of Figure 9.6. Most of the observations are on the correct side of the margin. However, a small subset of the observations are on the wrong side of the margin.
An observation can be not only on the wrong side of the margin, but also on the wrong side of the hyperplane. In fact, when there is no separating hyperplane, such a situation is inevitable. Observations on the wrong side of the hyperplane correspond to training observations that are misclassifed by the support vector classifer. The right-hand panel of Figure 9.6 illustrates such a scenario.
9.2.2 Details of the Support Vector Classifer
The support vector classifer classifes a test observation depending on which side of a hyperplane it lies. The hyperplane is chosen to correctly separate most of the training observations into the two classes, but may
vector classifer soft margin classifer
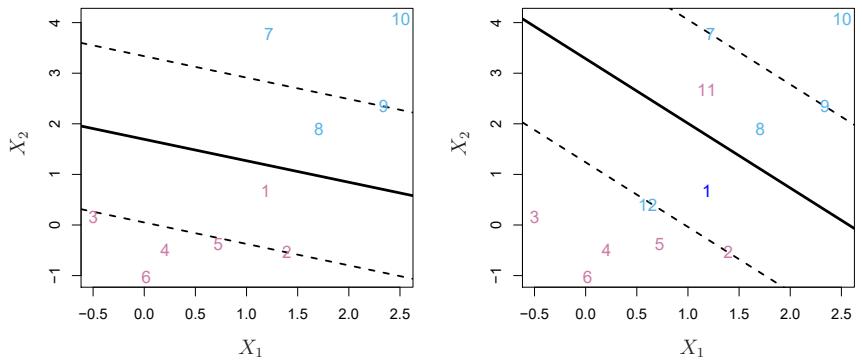
FIGURE 9.6. Left: A support vector classifer was ft to a small data set. The hyperplane is shown as a solid line and the margins are shown as dashed lines. Purple observations: Observations 3, 4, 5, and 6 are on the correct side of the margin, observation 2 is on the margin, and observation 1 is on the wrong side of the margin. Blue observations: Observations 7 and 10 are on the correct side of the margin, observation 9 is on the margin, and observation 8 is on the wrong side of the margin. No observations are on the wrong side of the hyperplane. Right: Same as left panel with two additional points, 11 and 12. These two observations are on the wrong side of the hyperplane and the wrong side of the margin.
misclassify a few observations. It is the solution to the optimization problem
\[\max\_{\beta\_0, \beta\_1, \dots, \beta\_p, \epsilon\_1, \dots, \epsilon\_n, M} M \tag{9.12}\]
\[\text{subject to } \sum\_{j=1}^{p} \beta\_j^2 = 1,\tag{9.13}\]
\[y\_i(\beta\_0 + \beta\_1 x\_{i1} + \beta\_2 x\_{i2} + \dots + \beta\_p x\_{ip}) \ge M(1 - \epsilon\_i),\qquad(9.14)\]
\[ \epsilon\_i \ge 0, \ \sum\_{i=1}^n \epsilon\_i \le C,\tag{9.15} \]
where C is a nonnegative tuning parameter. As in (9.11), M is the width of the margin; we seek to make this quantity as large as possible. In (9.14), ϵ1,…, ϵn are slack variables that allow individual observations to be on slack variable the wrong side of the margin or the hyperplane; we will explain them in greater detail momentarily. Once we have solved (9.12)–(9.15), we classify a test observation x∗ as before, by simply determining on which side of the hyperplane it lies. That is, we classify the test observation based on the sign of f(x∗) = β0 + β1x∗ 1 + ··· + βpx∗ p.
The problem (9.12)–(9.15) seems complex, but insight into its behavior can be made through a series of simple observations presented below. First of all, the slack variable ϵi tells us where the ith observation is located, relative to the hyperplane and relative to the margin. If ϵi = 0 then the ith observation is on the correct side of the margin, as we saw in Section 9.1.4. If ϵi > 0 then the ith observation is on the wrong side of the margin, and we say that the ith observation has violated the margin. If ϵi > 1 then it is on the wrong side of the hyperplane.
We now consider the role of the tuning parameter C. In (9.15), C bounds the sum of the ϵi’s, and so it determines the number and severity of the violations to the margin (and to the hyperplane) that we will tolerate. We can think of C as a budget for the amount that the margin can be violated by the n observations. If C = 0 then there is no budget for violations to the margin, and it must be the case that ϵ1 = ··· = ϵn = 0, in which case (9.12)–(9.15) simply amounts to the maximal margin hyperplane optimization problem (9.9)–(9.11). (Of course, a maximal margin hyperplane exists only if the two classes are separable.) For C > 0 no more than C observations can be on the wrong side of the hyperplane, because if an observation is on the wrong side of the hyperplane then ϵi > 1, and (9.15) requires that #n i=1 ϵi ≤ C. As the budget C increases, we become more tolerant of violations to the margin, and so the margin will widen. Conversely, as C decreases, we become less tolerant of violations to the margin and so the margin narrows. An example is shown in Figure 9.7.
In practice, C is treated as a tuning parameter that is generally chosen via cross-validation. As with the tuning parameters that we have seen throughout this book, C controls the bias-variance trade-of of the statistical learning technique. When C is small, we seek narrow margins that are rarely violated; this amounts to a classifer that is highly ft to the data, which may have low bias but high variance. On the other hand, when C is larger, the margin is wider and we allow more violations to it; this amounts to ftting the data less hard and obtaining a classifer that is potentially more biased but may have lower variance.
The optimization problem (9.12)–(9.15) has a very interesting property: it turns out that only observations that either lie on the margin or that violate the margin will afect the hyperplane, and hence the classifer obtained. In other words, an observation that lies strictly on the correct side of the margin does not afect the support vector classifer! Changing the position of that observation would not change the classifer at all, provided that its position remains on the correct side of the margin. Observations that lie directly on the margin, or on the wrong side of the margin for their class, are known as support vectors. These observations do afect the support vector classifer.
The fact that only support vectors afect the classifer is in line with our previous assertion that C controls the bias-variance trade-of of the support vector classifer. When the tuning parameter C is large, then the margin is wide, many observations violate the margin, and so there are many support vectors. In this case, many observations are involved in determining the hyperplane. The top left panel in Figure 9.7 illustrates this setting: this classifer has low variance (since many observations are support vectors) but potentially high bias. In contrast, if C is small, then there will be fewer support vectors and hence the resulting classifer will have low bias but high variance. The bottom right panel in Figure 9.7 illustrates this setting, with only eight support vectors.
The fact that the support vector classifer’s decision rule is based only on a potentially small subset of the training observations (the support vectors) means that it is quite robust to the behavior of observations that are far away from the hyperplane. This property is distinct from some of
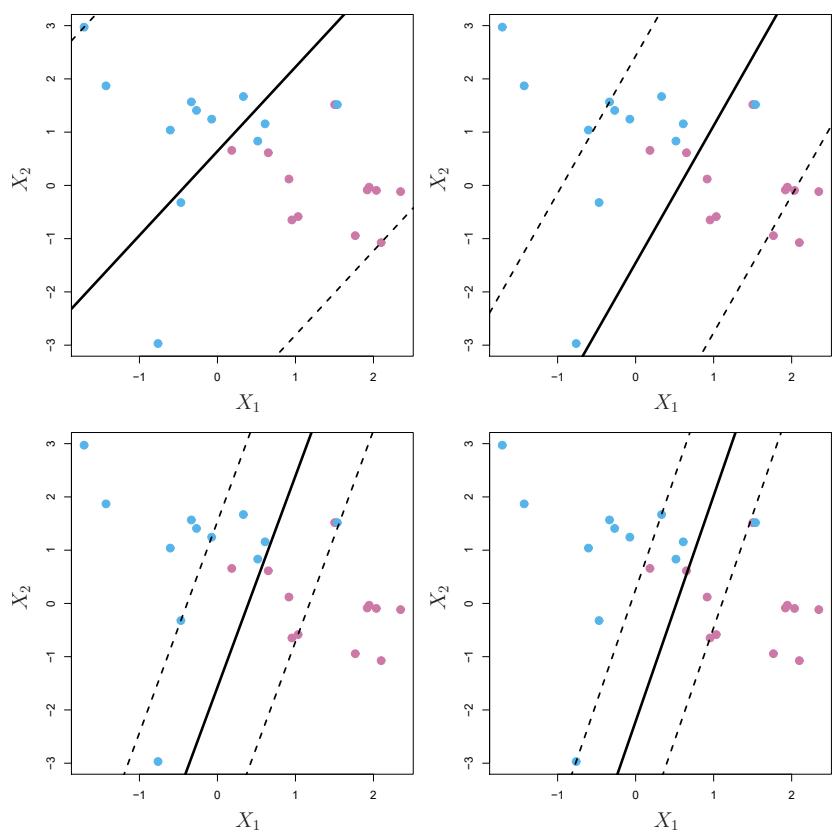
FIGURE 9.7. A support vector classifer was ft using four diferent values of the tuning parameter C in (9.12)–(9.15). The largest value of C was used in the top left panel, and smaller values were used in the top right, bottom left, and bottom right panels. When C is large, then there is a high tolerance for observations being on the wrong side of the margin, and so the margin will be large. As C decreases, the tolerance for observations being on the wrong side of the margin decreases, and the margin narrows.
the other classifcation methods that we have seen in preceding chapters, such as linear discriminant analysis. Recall that the LDA classifcation rule depends on the mean of all of the observations within each class, as well as the within-class covariance matrix computed using all of the observations. In contrast, logistic regression, unlike LDA, has very low sensitivity to observations far from the decision boundary. In fact we will see in Section 9.5 that the support vector classifer and logistic regression are closely related.
9.3 Support Vector Machines
We frst discuss a general mechanism for converting a linear classifer into one that produces non-linear decision boundaries. We then introduce the support vector machine, which does this in an automatic way.
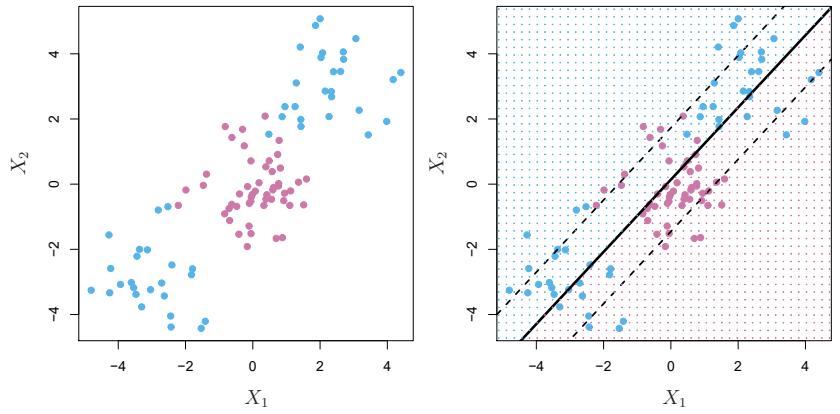
FIGURE 9.8. Left: The observations fall into two classes, with a non-linear boundary between them. Right: The support vector classifer seeks a linear boundary, and consequently performs very poorly.
9.3.1 Classifcation with Non-Linear Decision Boundaries
The support vector classifer is a natural approach for classifcation in the two-class setting, if the boundary between the two classes is linear. However, in practice we are sometimes faced with non-linear class boundaries. For instance, consider the data in the left-hand panel of Figure 9.8. It is clear that a support vector classifer or any linear classifer will perform poorly here. Indeed, the support vector classifer shown in the right-hand panel of Figure 9.8 is useless here.
In Chapter 7, we are faced with an analogous situation. We see there that the performance of linear regression can sufer when there is a nonlinear relationship between the predictors and the outcome. In that case, we consider enlarging the feature space using functions of the predictors, such as quadratic and cubic terms, in order to address this non-linearity. In the case of the support vector classifer, we could address the problem of possibly non-linear boundaries between classes in a similar way, by enlarging the feature space using quadratic, cubic, and even higher-order polynomial functions of the predictors. For instance, rather than ftting a support vector classifer using p features
\[X\_1, X\_2, \dots, X\_p,\]
we could instead ft a support vector classifer using 2p features
\[X\_1, X\_1^2, X\_2, X\_2^2, \dots, X\_p, X\_p^2.\]
Then (9.12)–(9.15) would become
\[\begin{aligned} \underset{\beta\_0, \beta\_{11}, \beta\_{12}, \dots, \beta\_{p1}, \beta\_{p2}, \epsilon\_1, \dots, \epsilon\_n, M}{\text{subject to } y\_i} \quad &M\\ \text{subject to } y\_i \left(\beta\_0 + \sum\_{j=1}^p \beta\_{j1} x\_{ij} + \sum\_{j=1}^p \beta\_{j2} x\_{ij}^2 \right) &\ge M(1 - \epsilon\_i),\\ \sum\_{i=1}^n \epsilon\_i \le C, \quad \epsilon\_i \ge 0, \quad &\sum\_{j=1}^p \sum\_{k=1}^2 \beta\_{jk}^2 = 1. \end{aligned}\]
Why does this lead to a non-linear decision boundary? In the enlarged feature space, the decision boundary that results from (9.16) is in fact linear. But in the original feature space, the decision boundary is of the form q(x)=0, where q is a quadratic polynomial, and its solutions are generally non-linear. One might additionally want to enlarge the feature space with higher-order polynomial terms, or with interaction terms of the form XjXj′ for j ̸= j′ . Alternatively, other functions of the predictors could be considered rather than polynomials. It is not hard to see that there are many possible ways to enlarge the feature space, and that unless we are careful, we could end up with a huge number of features. Then computations would become unmanageable. The support vector machine, which we present next, allows us to enlarge the feature space used by the support vector classifer in a way that leads to efcient computations.
9.3.2 The Support Vector Machine
The support vector machine (SVM) is an extension of the support vector support vector machine classifer that results from enlarging the feature space in a specifc way, using kernels. We will now discuss this extension, the details of which are somewhat complex and beyond the scope of this book. However, the main kernel idea is described in Section 9.3.1: we may want to enlarge our feature space in order to accommodate a non-linear boundary between the classes. The kernel approach that we describe here is simply an efcient computational approach for enacting this idea.
We have not discussed exactly how the support vector classifer is computed because the details become somewhat technical. However, it turns out that the solution to the support vector classifer problem (9.12)–(9.15) involves only the inner products of the observations (as opposed to the observations themselves). The inner product of two r-vectors a and b is defned as ⟨a, b⟩ = #r i=1 aibi. Thus the inner product of two observations xi, xi′ is given by
\[ \langle x\_i, x\_{i'} \rangle = \sum\_{j=1}^p x\_{ij} x\_{i'j}.\tag{9.17} \]
It can be shown that
• The linear support vector classifer can be represented as
\[f(x) = \beta\_0 + \sum\_{i=1}^{n} \alpha\_i \langle x, x\_i \rangle,\tag{9.18}\]
where there are n parameters αi, i = 1,…,n, one per training observation.
• To estimate the parameters α1,…, αn and β0, all we need are the 5n 2 6 inner products ⟨xi, xi′ ⟩ between all pairs of training observations. (The notation 5n 2 6 means n(n − 1)/2, and gives the number of pairs among a set of n items.)
Notice that in (9.18), in order to evaluate the function f(x), we need to compute the inner product between the new point x and each of the training points xi. However, it turns out that αi is nonzero only for the support vectors in the solution—that is, if a training observation is not a support vector, then its αi equals zero. So if S is the collection of indices of these support points, we can rewrite any solution function of the form (9.18) as
\[f(x) = \beta\_0 + \sum\_{i \in \mathcal{S}} \alpha\_i \langle x, x\_i \rangle,\tag{9.19}\]
which typically involves far fewer terms than in (9.18).2
To summarize, in representing the linear classifer f(x), and in computing its coefcients, all we need are inner products.
Now suppose that every time the inner product (9.17) appears in the representation (9.18), or in a calculation of the solution for the support vector classifer, we replace it with a generalization of the inner product of the form
\[K(x\_i, x\_{i'}),\tag{9.20}\]
where K is some function that we will refer to as a kernel. A kernel is a kernel function that quantifes the similarity of two observations. For instance, we could simply take
\[K(x\_i, x\_{i'}) = \sum\_{j=1}^{p} x\_{ij} x\_{i'j},\tag{9.21}\]
which would just give us back the support vector classifer. Equation 9.21 is known as a linear kernel because the support vector classifer is linear in the features; the linear kernel essentially quantifes the similarity of a pair of observations using Pearson (standard) correlation. But one could instead choose another form for (9.20). For instance, one could replace every instance of #p j=1 xijxi′j with the quantity
\[K(x\_i, x\_{i'}) = (1 + \sum\_{j=1}^p x\_{ij} x\_{i'j})^d. \tag{9.22}\]
This is known as a polynomial kernel of degree d, where d is a positive polynomial kernel integer. Using such a kernel with d > 1, instead of the standard linear kernel (9.21), in the support vector classifer algorithm leads to a much more fexible decision boundary. It essentially amounts to ftting a support vector
2By expanding each of the inner products in (9.19), it is easy to see that f(x) is a linear function of the coordinates of x. Doing so also establishes the correspondence between the αi and the original parameters βj .
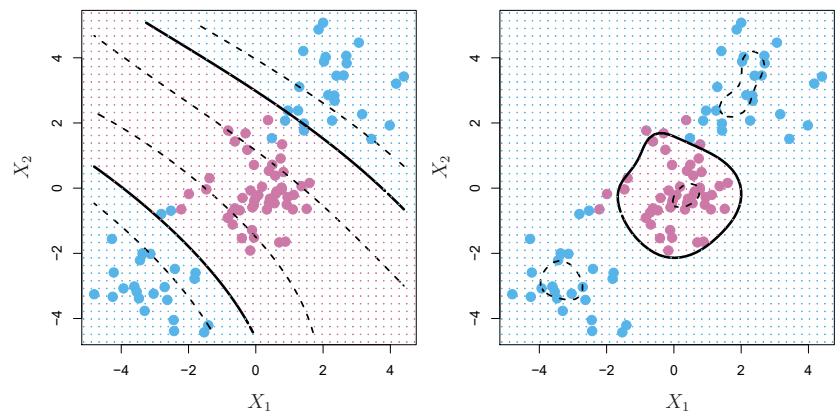
FIGURE 9.9. Left: An SVM with a polynomial kernel of degree 3 is applied to the non-linear data from Figure 9.8, resulting in a far more appropriate decision rule. Right: An SVM with a radial kernel is applied. In this example, either kernel is capable of capturing the decision boundary.
classifer in a higher-dimensional space involving polynomials of degree d, rather than in the original feature space. When the support vector classifer is combined with a non-linear kernel such as (9.22), the resulting classifer is known as a support vector machine. Note that in this case the (non-linear) function has the form
\[f(x) = \beta\_0 + \sum\_{i \in \mathcal{S}} \alpha\_i K(x, x\_i). \tag{9.23}\]
The left-hand panel of Figure 9.9 shows an example of an SVM with a polynomial kernel applied to the non-linear data from Figure 9.8. The ft is a substantial improvement over the linear support vector classifer. When d = 1, then the SVM reduces to the support vector classifer seen earlier in this chapter.
The polynomial kernel shown in (9.22) is one example of a possible non-linear kernel, but alternatives abound. Another popular choice is the radial kernel, which takes the form radial kernel
\[K(x\_i, x\_{i'}) = \exp(-\gamma \sum\_{j=1}^p (x\_{ij} - x\_{i'j})^2). \tag{9.24}\]
In (9.24), γ is a positive constant. The right-hand panel of Figure 9.9 shows an example of an SVM with a radial kernel on this non-linear data; it also does a good job in separating the two classes.
How does the radial kernel (9.24) actually work? If a given test observation x∗ = (x∗ 1,…,x∗ p)T is far from a training observation xi in terms of Euclidean distance, then #p j=1(x∗ j −xij )2 will be large, and so K(x∗, xi) = exp(−γ #p j=1(x∗ j − xij )2) will be tiny. This means that in (9.23), xi will play virtually no role in f(x∗). Recall that the predicted class label for the test observation x∗ is based on the sign of f(x∗). In other words, training observations that are far from x∗ will play essentially no role in the predicted class label for x∗. This means that the radial kernel has very local
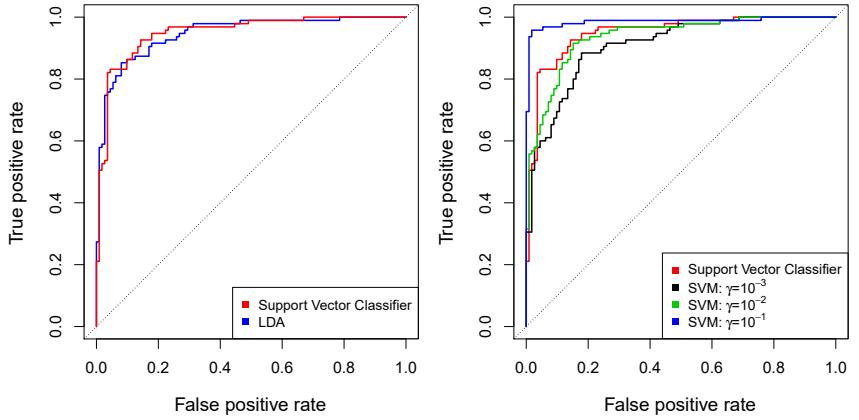
FIGURE 9.10. ROC curves for the Heart data training set. Left: The support vector classifer and LDA are compared. Right: The support vector classifer is compared to an SVM using a radial basis kernel with γ = 10−3, 10−2, and 10−1.
behavior, in the sense that only nearby training observations have an efect on the class label of a test observation.
What is the advantage of using a kernel rather than simply enlarging the feature space using functions of the original features, as in (9.16)? One advantage is computational, and it amounts to the fact that using kernels, one need only compute K(xi, x′ i) for all 5n 2 6 distinct pairs i, i′ . This can be done without explicitly working in the enlarged feature space. This is important because in many applications of SVMs, the enlarged feature space is so large that computations are intractable. For some kernels, such as the radial kernel (9.24), the feature space is implicit and infnite-dimensional, so we could never do the computations there anyway!
9.3.3 An Application to the Heart Disease Data
In Chapter 8 we apply decision trees and related methods to the Heart data. The aim is to use 13 predictors such as Age, Sex, and Chol in order to predict whether an individual has heart disease. We now investigate how an SVM compares to LDA on this data. After removing 6 missing observations, the data consist of 297 subjects, which we randomly split into 207 training and 90 test observations.
We frst ft LDA and the support vector classifer to the training data. Note that the support vector classifer is equivalent to an SVM using a polynomial kernel of degree d = 1. The left-hand panel of Figure 9.10 displays ROC curves (described in Section 4.4.2) for the training set predictions for both LDA and the support vector classifer. Both classifers compute scores of the form ˆf(X) = βˆ0 + βˆ1X1 + βˆ2X2 + ··· + βˆpXp for each observation. For any given cutof t, we classify observations into the heart disease or no heart disease categories depending on whether ˆf(X) < t or ˆf(X) ≥ t. The ROC curve is obtained by forming these predictions and computing the false positive and true positive rates for a range of values of t. An optimal classifer will hug the top left corner of the ROC plot. In this instance
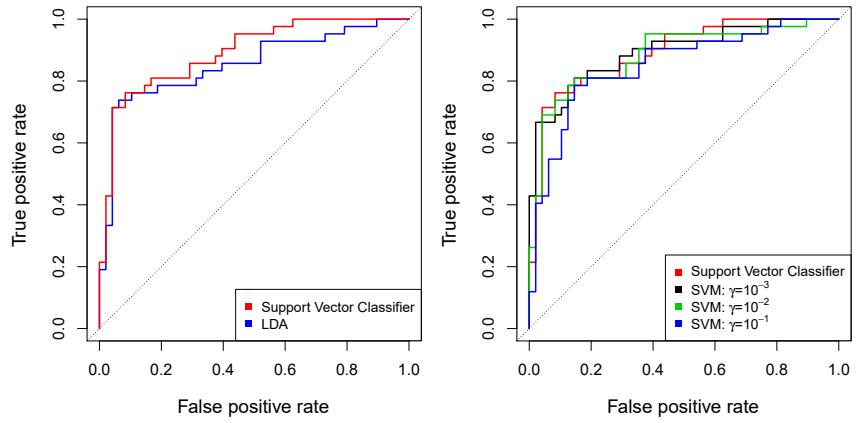
FIGURE 9.11. ROC curves for the test set of the Heart data. Left: The support vector classifer and LDA are compared. Right: The support vector classifer is compared to an SVM using a radial basis kernel with γ = 10−3, 10−2, and 10−1.
LDA and the support vector classifer both perform well, though there is a suggestion that the support vector classifer may be slightly superior.
The right-hand panel of Figure 9.10 displays ROC curves for SVMs using a radial kernel, with various values of γ. As γ increases and the ft becomes more non-linear, the ROC curves improve. Using γ = 10−1 appears to give an almost perfect ROC curve. However, these curves represent training error rates, which can be misleading in terms of performance on new test data. Figure 9.11 displays ROC curves computed on the 90 test observations. We observe some diferences from the training ROC curves. In the left-hand panel of Figure 9.11, the support vector classifer appears to have a small advantage over LDA (although these diferences are not statistically signifcant). In the right-hand panel, the SVM using γ = 10−1, which showed the best results on the training data, produces the worst estimates on the test data. This is once again evidence that while a more fexible method will often produce lower training error rates, this does not necessarily lead to improved performance on test data. The SVMs with γ = 10−2 and γ = 10−3 perform comparably to the support vector classifer, and all three outperform the SVM with γ = 10−1.
9.4 SVMs with More than Two Classes
So far, our discussion has been limited to the case of binary classifcation: that is, classifcation in the two-class setting. How can we extend SVMs to the more general case where we have some arbitrary number of classes? It turns out that the concept of separating hyperplanes upon which SVMs are based does not lend itself naturally to more than two classes. Though a number of proposals for extending SVMs to the K-class case have been made, the two most popular are the one-versus-one and one-versus-all approaches. We briefy discuss those two approaches here.
9.4.1 One-Versus-One Classifcation
Suppose that we would like to perform classifcation using SVMs, and there are K > 2 classes. A one-versus-one or all-pairs approach constructs 5K 2 6 SVMs, each of which compares a pair of classes. For example, one such one SVM might compare the kth class, coded as +1, to the k′ th class, coded as −1. We classify a test observation using each of the 5K 2 6 classifers, and we tally the number of times that the test observation is assigned to each of the K classes. The fnal classifcation is performed by assigning the test observation to the class to which it was most frequently assigned in these 5K 2 6 pairwise classifcations.
9.4.2 One-Versus-All Classifcation
The one-versus-all approach (also referred to as one-versus-rest) is an al- one-versusternative procedure for applying SVMs in the case of K > 2 classes. We ft K SVMs, each time comparing one of the K classes to the remaining K − 1 classes. Let β0k, β1k,…, βpk denote the parameters that result from ftting an SVM comparing the kth class (coded as +1) to the others (coded as −1). Let x∗ denote a test observation. We assign the observation to the class for which β0k +β1kx∗ 1 +β2kx∗ 2 +···+βpkx∗ p is largest, as this amounts to a high level of confdence that the test observation belongs to the kth class rather than to any of the other classes.
all one-versusrest
9.5 Relationship to Logistic Regression
When SVMs were frst introduced in the mid-1990s, they made quite a splash in the statistical and machine learning communities. This was due in part to their good performance, good marketing, and also to the fact that the underlying approach seemed both novel and mysterious. The idea of fnding a hyperplane that separates the data as well as possible, while allowing some violations to this separation, seemed distinctly diferent from classical approaches for classifcation, such as logistic regression and linear discriminant analysis. Moreover, the idea of using a kernel to expand the feature space in order to accommodate non-linear class boundaries appeared to be a unique and valuable characteristic.
However, since that time, deep connections between SVMs and other more classical statistical methods have emerged. It turns out that one can rewrite the criterion (9.12)–(9.15) for ftting the support vector classifer f(X) = β0 + β1X1 + ··· + βpXp as
\[\underset{\beta\_0, \beta\_1, \dots, \beta\_p}{\text{minimize}} \left\{ \sum\_{i=1}^n \max\left[0, 1 - y\_i f(x\_i)\right] + \lambda \sum\_{j=1}^p \beta\_j^2 \right\},\tag{9.25}\]
where λ is a nonnegative tuning parameter. When λ is large then β1,…, βp are small, more violations to the margin are tolerated, and a low-variance but high-bias classifer will result. When λ is small then few violations to the margin will occur; this amounts to a high-variance but low-bias
classifer. Thus, a small value of λ in (9.25) amounts to a small value of C in (9.15). Note that the λ #p j=1 β2 j term in (9.25) is the ridge penalty term from Section 6.2.1, and plays a similar role in controlling the bias-variance trade-of for the support vector classifer.
Now (9.25) takes the “Loss + Penalty” form that we have seen repeatedly throughout this book:
\[\underset{\beta\_0, \beta\_1, \dots, \beta\_p}{\text{minimize}} \left\{ L(\mathbf{X}, \mathbf{y}, \beta) + \lambda P(\beta) \right\}. \tag{9.26}\]
In (9.26), L(X, y, β) is some loss function quantifying the extent to which the model, parametrized by β, fts the data (X, y), and P(β) is a penalty function on the parameter vector β whose efect is controlled by a nonnegative tuning parameter λ. For instance, ridge regression and the lasso both take this form with
\[L(\mathbf{X}, \mathbf{y}, \boldsymbol{\beta}) = \sum\_{i=1}^{n} \left( y\_i - \beta\_0 - \sum\_{j=1}^{p} x\_{ij}\beta\_j \right)^2\]
and with P(β) = #p j=1 β2 j for ridge regression and P(β) = #p j=1 |βj | for the lasso. In the case of (9.25) the loss function instead takes the form
\[L(\mathbf{X}, \mathbf{y}, \boldsymbol{\beta}) = \sum\_{i=1}^{n} \max\left[0, 1 - y\_i(\beta\_0 + \beta\_1 x\_{i1} + \dots + \beta\_p x\_{ip})\right].\]
This is known as hinge loss, and is depicted in Figure 9.12. However, it hinge loss turns out that the hinge loss function is closely related to the loss function used in logistic regression, also shown in Figure 9.12.
An interesting characteristic of the support vector classifer is that only support vectors play a role in the classifer obtained; observations on the correct side of the margin do not afect it. This is due to the fact that the loss function shown in Figure 9.12 is exactly zero for observations for which yi(β0 + β1xi1 + ··· + βpxip) ≥ 1; these correspond to observations that are on the correct side of the margin.3 In contrast, the loss function for logistic regression shown in Figure 9.12 is not exactly zero anywhere. But it is very small for observations that are far from the decision boundary. Due to the similarities between their loss functions, logistic regression and the support vector classifer often give very similar results. When the classes are well separated, SVMs tend to behave better than logistic regression; in more overlapping regimes, logistic regression is often preferred.
When the support vector classifer and SVM were frst introduced, it was thought that the tuning parameter C in (9.15) was an unimportant “nuisance” parameter that could be set to some default value, like 1. However, the “Loss + Penalty” formulation (9.25) for the support vector classifer indicates that this is not the case. The choice of tuning parameter is very important and determines the extent to which the model underfts or overfts the data, as illustrated, for example, in Figure 9.7.
3With this hinge-loss + penalty representation, the margin corresponds to the value one, and the width of the margin is determined by !β2 j .
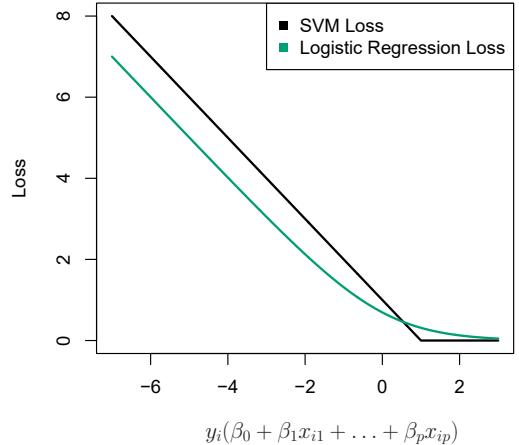
FIGURE 9.12. The SVM and logistic regression loss functions are compared, as a function of yi(β0 +β1xi1 +···+βpxip). When yi(β0 +β1xi1 +···+βpxip) is greater than 1, then the SVM loss is zero, since this corresponds to an observation that is on the correct side of the margin. Overall, the two loss functions have quite similar behavior.
We have established that the support vector classifer is closely related to logistic regression and other preexisting statistical methods. Is the SVM unique in its use of kernels to enlarge the feature space to accommodate non-linear class boundaries? The answer to this question is “no”. We could just as well perform logistic regression or many of the other classifcation methods seen in this book using non-linear kernels; this is closely related to some of the non-linear approaches seen in Chapter 7. However, for historical reasons, the use of non-linear kernels is much more widespread in the context of SVMs than in the context of logistic regression or other methods.
Though we have not addressed it here, there is in fact an extension of the SVM for regression (i.e. for a quantitative rather than a qualitative response), called support vector regression. In Chapter 3, we saw that support least squares regression seeks coefcients β0, β1,…, βp such that the sum of squared residuals is as small as possible. (Recall from Chapter 3 that residuals are defned as yi − β0 − β1xi1 − ··· − βpxip.) Support vector regression instead seeks coefcients that minimize a diferent type of loss, where only residuals larger in absolute value than some positive constant contribute to the loss function. This is an extension of the margin used in support vector classifers to the regression setting.
vector regression
9.6 Lab: Support Vector Machines
In this lab, we use the sklearn.svm library to demonstrate the support vector classifer and the support vector machine.
We import some of our usual libraries.
In [1]: import numpy as np
from matplotlib.pyplot import subplots, cm
import sklearn.model_selection as skm
from ISLP import load_data, confusion_tableWe also collect the new imports needed for this lab.
In [2]: from sklearn.svm import SVC
from ISLP.svm import plot as plot_svm
from sklearn.metrics import RocCurveDisplayWe will use the function RocCurveDisplay.from_estimator() to produce RocCurve several ROC plots, using a shorthand roc_curve.
In [3]: roc_curve = RocCurveDisplay.from_estimator # shorthand
Display.from_ estimator()
9.6.1 Support Vector Classifer
We now use the SupportVectorClassifier() function (abbreviated SVC()) SupportVector Classifier() from sklearn to ft the support vector classifer for a given value of the parameter C. The C argument allows us to specify the cost of a violation to the margin. When the cost argument is small, then the margins will be wide and many support vectors will be on the margin or will violate the margin. When the C argument is large, then the margins will be narrow and there will be few support vectors on the margin or violating the margin.
Here we demonstrate the use of SVC() on a two-dimensional example, so that we can plot the resulting decision boundary. We begin by generating the observations, which belong to two classes, and checking whether the classes are linearly separable.
In [4]: rng = np.random.default_rng(1)
X = rng.standard_normal((50, 2))
y = np.array([-1]*25+[1]*25)
X[y==1] += 1
fig, ax = subplots(figsize=(8,8))
ax.scatter(X[:,0],
X[:,1],
c=y,
cmap=cm.coolwarm);They are not. We now ft the classifer.
In [5]: svm_linear = SVC(C=10, kernel='linear')
svm_linear.fit(X, y)Out[5]: SVC(C=10, kernel=‘linear’)
The support vector classifer with two features can be visualized by plotting values of its decision function. We have included a function for this in decision function the ISLP package (inspired by a similar example in the sklearn docs).
388 9. Support Vector Machines
In [6]: fig, ax = subplots(figsize=(8,8))
plot_svm(X,
y,
svm_linear,
ax=ax)The decision boundary between the two classes is linear (because we used the argument kernel=‘linear’). The support vectors are marked with + and the remaining observations are plotted as circles.
What if we instead used a smaller value of the cost parameter?
In [7]: svm_linear_small = SVC(C=0.1, kernel='linear')
svm_linear_small.fit(X, y)
fig, ax = subplots(figsize=(8,8))
plot_svm(X,
y,
svm_linear_small,
ax=ax)With a smaller value of the cost parameter, we obtain a larger number of support vectors, because the margin is now wider. For linear kernels, we can extract the coefcients of the linear decision boundary as follows:
In [8]: svm_linear.coef_Out[8]: array([[1.173 , 0.7734]])Since the support vector machine is an estimator in sklearn, we can use the usual machinery to tune it.
In [9]: kfold = skm.KFold(5,
random_state=0,
shuffle=True)
grid = skm.GridSearchCV(svm_linear,
{'C':[0.001,0.01,0.1,1,5,10,100]},
refit=True,
cv=kfold,
scoring='accuracy')
grid.fit(X, y)
grid.best_params_Out[9]: {‘C’: 1}
We can easily access the cross-validation errors for each of these models in grid.cv_results_. This prints out a lot of detail, so we extract the accuracy results only.
In [10]: grid.cv_results_[('mean_test_score')]Out[10]: array([0.46, 0.46, 0.72, 0.74, 0.74, 0.74, 0.74])We see that C=1 results in the highest cross-validation accuracy of 0.74, though the accuracy is the same for several values of C. The classifer grid.best_estimator_ can be used to predict the class label on a set of test observations. Let’s generate a test data set.
In [11]: X_test = rng.standard_normal((20, 2))
y_test = np.array([-1]*10+[1]*10)
X_test[y_test==1] += 1Now we predict the class labels of these test observations. Here we use the best model selected by cross-validation in order to make the predictions.
In [12]: best_ = grid.best_estimator_
y_test_hat = best_.predict(X_test)
confusion_table(y_test_hat, y_test)Out[12]: Truth -1 1
Predicted
-1 8 4
126Thus, with this value of C, 70% of the test observations are correctly classifed. What if we had instead used C=0.001?
In [13]: svm_ = SVC(C=0.001,
kernel='linear').fit(X, y)
y_test_hat = svm_.predict(X_test)
confusion_table(y_test_hat, y_test)Out[13]: Truth -1 1
Predicted
-1 2 0
1 8 10In this case 60% of test observations are correctly classifed.
We now consider a situation in which the two classes are linearly separable. Then we can fnd an optimal separating hyperplane using the SVC() estimator. We frst further separate the two classes in our simulated data so that they are linearly separable:
In [14]: X[y==1] += 1.9;
fig, ax = subplots(figsize=(8,8))
ax.scatter(X[:,0], X[:,1], c=y, cmap=cm.coolwarm);Now the observations are just barely linearly separable.
In [15]: svm_ = SVC(C=1e5, kernel='linear').fit(X, y)
y_hat = svm_.predict(X)
confusion_table(y_hat, y)Out[15]: Truth -1 1
Predicted
-1 25 0
1 0 25We ft the support vector classifer and plot the resulting hyperplane, using a very large value of C so that no observations are misclassifed.
In [16]: fig, ax = subplots(figsize=(8,8))
plot_svm(X,
y,
svm_,
ax=ax)Indeed no training errors were made and only three support vectors were used. In fact, the large value of C also means that these three support points are on the margin, and defne it. One may wonder how good the classifer could be on test data that depends on only three data points! We now try a smaller value of C.
In [17]: svm_ = SVC(C=0.1, kernel='linear').fit(X, y)
y_hat = svm_.predict(X)
confusion_table(y_hat, y)Out[17]: Truth -1 1
Predicted
-1 25 0
1 0 25Using C=0.1, we again do not misclassify any training observations, but we also obtain a much wider margin and make use of twelve support vectors. These jointly defne the orientation of the decision boundary, and since there are more of them, it is more stable. It seems possible that this model will perform better on test data than the model with C=1e5 (and indeed, a simple experiment with a large test set would bear this out).
In [18]: fig, ax = subplots(figsize=(8,8))
plot_svm(X,
y,
svm_,
ax=ax)9.6.2 Support Vector Machine
In order to ft an SVM using a non-linear kernel, we once again use the SVC() estimator. However, now we use a diferent value of the parameter kernel. To ft an SVM with a polynomial kernel we use kernel=“poly”, and to ft an SVM with a radial kernel we use kernel=“rbf”. In the former case we also use the degree argument to specify a degree for the polynomial kernel (this is d in (9.22)), and in the latter case we use gamma to specify a value of γ for the radial basis kernel (9.24).
We frst generate some data with a non-linear class boundary, as follows:
In [19]: X = rng.standard_normal((200, 2))
X[:100] += 2
X[100:150] -= 2
y = np.array([1]*150+[2]*50)Plotting the data makes it clear that the class boundary is indeed nonlinear.
In [20]: fig, ax = subplots(figsize=(8,8))
ax.scatter(X[:,0],
X[:,1],
c=y,
cmap=cm.coolwarm)Out[20]: <matplotlib.collections.PathCollection at 0x7faa9ba52eb0 >
The data is randomly split into training and testing groups. We then ft the training data using the SVC() estimator with a radial kernel and γ = 1:
In [21]: (X_train,
X_test,
y_train,
y_test) = skm.train_test_split(X,
y,
test_size=0.5,
random_state=0)
svm_rbf = SVC(kernel="rbf", gamma=1, C=1)
svm_rbf.fit(X_train, y_train)The plot shows that the resulting SVM has a decidedly non-linear boundary.
In [22]: fig, ax = subplots(figsize=(8,8))
plot_svm(X_train,
y_train,
svm_rbf,
ax=ax)We can see from the fgure that there are a fair number of training errors in this SVM ft. If we increase the value of C, we can reduce the number of training errors. However, this comes at the price of a more irregular decision boundary that seems to be at risk of overftting the data.
In [23]: svm_rbf = SVC(kernel="rbf", gamma=1, C=1e5)
svm_rbf.fit(X_train, y_train)
fig, ax = subplots(figsize=(8,8))
plot_svm(X_train,
y_train,
svm_rbf,
ax=ax)We can perform cross-validation using skm.GridSearchCV() to select the best choice of γ and C for an SVM with a radial kernel:
In [24]: kfold = skm.KFold(5,
random_state=0,
shuffle=True)
grid = skm.GridSearchCV(svm_rbf,
{'C':[0.1,1,10,100,1000],
'gamma':[0.5,1,2,3,4]},
refit=True,
cv=kfold,
scoring='accuracy');
grid.fit(X_train, y_train)
grid.best_params_Out[24]: {‘C’: 100, ‘gamma’: 1}
The best choice of parameters under fve-fold CV is achieved at C=1 and gamma=0.5, though several other values also achieve the same value.
In [25]: best_svm = grid.best_estimator_
fig, ax = subplots(figsize=(8,8))
plot_svm(X_train,392 9. Support Vector Machines
y_train,
best_svm,
ax=ax)
y_hat_test = best_svm.predict(X_test)
confusion_table(y_hat_test, y_test)Out[25]: Truth 1 2
Predicted
1 69 6
2 6 19With these parameters, 12% of test observations are misclassifed by this SVM.
9.6.3 ROC Curves
SVMs and support vector classifers output class labels for each observation. However, it is also possible to obtain ftted values for each observation, which are the numerical scores used to obtain the class labels. For instance, in the case of a support vector classifer, the ftted value for an observation X = (X1, X2,…,Xp)T takes the form βˆ0 +βˆ1X1 +βˆ2X2 +…+βˆpXp. For an SVM with a non-linear kernel, the equation that yields the ftted value is given in (9.23). The sign of the ftted value determines on which side of the decision boundary the observation lies. Therefore, the relationship between the ftted value and the class prediction for a given observation is simple: if the ftted value exceeds zero then the observation is assigned to one class, and if it is less than zero then it is assigned to the other. By changing this threshold from zero to some positive value, we skew the classifcations in favor of one class versus the other. By considering a range of these thresholds, positive and negative, we produce the ingredients for a ROC plot. We can access these values by calling the decision_function() .function_ method of a ftted SVM estimator. decision()
The function ROCCurveDisplay.from_estimator() (which we have abbreviated to roc_curve()) will produce a plot of a ROC curve. It takes a ftted roc_curve() estimator as its frst argument, followed by a model matrix X and labels y. The argument name is used in the legend, while color is used for the color of the line. Results are plotted on our axis object ax.
In [26]: fig, ax = subplots(figsize=(8,8))
roc_curve(best_svm,
X_train,
y_train,
name='Training',
color='r',
ax=ax);In this example, the SVM appears to provide accurate predictions. By increasing γ we can produce a more fexible ft and generate further improvements in accuracy.
In [27]: svm_flex = SVC(kernel="rbf",
gamma=50,C=1)
svm_flex.fit(X_train, y_train)
fig, ax = subplots(figsize=(8,8))
roc_curve(svm_flex,
X_train,
y_train,
name='Training $\gamma=50$',
color='r',
ax=ax);However, these ROC curves are all on the training data. We are really more interested in the level of prediction accuracy on the test data. When we compute the ROC curves on the test data, the model with γ = 0.5 appears to provide the most accurate results.
In [28]: roc_curve(svm_flex,
X_test,
y_test,
name='Test $\gamma=50$',
color='b',
ax=ax)
fig;Let’s look at our tuned SVM.
In [29]: fig, ax = subplots(figsize=(8,8))
for (X_, y_, c, name) in zip(
(X_train, X_test),
(y_train, y_test),
('r', 'b'),
('CV tuned on training',
'CV tuned on test')):
roc_curve(best_svm,
X_,
y_,
name=name,
ax=ax,
color=c)9.6.4 SVM with Multiple Classes
If the response is a factor containing more than two levels, then the SVC() function will perform multi-class classifcation using either the one-versusone approach (when decision_function_shape==‘ovo’) or one-versus-rest4 (when decision_function_shape==‘ovr’). We explore that setting briefy here by generating a third class of observations.
In [30]: rng = np.random.default_rng(123)
X = np.vstack([X, rng.standard_normal((50, 2))])
y = np.hstack([y, [0]*50])
X[y==0,1] += 2
fig, ax = subplots(figsize=(8,8))
ax.scatter(X[:,0], X[:,1], c=y, cmap=cm.coolwarm);4One-versus-rest is also known as one-versus-all.
394 9. Support Vector Machines
We now ft an SVM to the data:
In [31]: svm_rbf_3 = SVC(kernel="rbf",
C=10,
gamma=1,
decision_function_shape='ovo');
svm_rbf_3.fit(X, y)
fig, ax = subplots(figsize=(8,8))
plot_svm(X,
y,
svm_rbf_3,
scatter_cmap=cm.tab10,
ax=ax)The sklearn.svm library can also be used to perform support vector regression with a numerical response using the estimator SupportVector-Regression(). SupportVector
Regression()
9.6.5 Application to Gene Expression Data
We now examine the Khan data set, which consists of a number of tissue samples corresponding to four distinct types of small round blue cell tumors. For each tissue sample, gene expression measurements are available. The data set consists of training data, xtrain and ytrain, and testing data, xtest and ytest.
We examine the dimension of the data:
In [32]: Khan = load_data('Khan')
Khan['xtrain'].shape, Khan['xtest'].shapeOut[32]: ((63, 2308), (20, 2308))This data set consists of expression measurements for 2,308 genes. The training and test sets consist of 63 and 20 observations, respectively.
We will use a support vector approach to predict cancer subtype using gene expression measurements. In this data set, there is a very large number of features relative to the number of observations. This suggests that we should use a linear kernel, because the additional fexibility that will result from using a polynomial or radial kernel is unnecessary.
In [33]: khan_linear = SVC(kernel='linear', C=10)
khan_linear.fit(Khan['xtrain'], Khan['ytrain'])
confusion_table(khan_linear.predict(Khan['xtrain']),
Khan['ytrain'])Out[33]: Truth 1 2 3 4
Predicted
1 8000
2 0 23 0 0
3 0 0 12 0
4 0 0 0 20We see that there are no training errors. In fact, this is not surprising, because the large number of variables relative to the number of observations implies that it is easy to fnd hyperplanes that fully separate the classes. We are more interested in the support vector classifer’s performance on the test observations.
In [34]: confusion_table(khan_linear.predict(Khan['xtest']),
Khan['ytest'])
Out[34]: Truth 1 2 3 4
Predicted
1 30002 0620 3 0040 4 0005
We see that using C=10 yields two test set errors on these data.
9.7 Exercises
Conceptual
- This problem involves hyperplanes in two dimensions.
- Sketch the hyperplane 1+3X1 − X2 = 0. Indicate the set of points for which 1+3X1 − X2 > 0, as well as the set of points for which 1+3X1 − X2 < 0.
- On the same plot, sketch the hyperplane −2 + X1 + 2X2 = 0. Indicate the set of points for which −2 + X1 + 2X2 > 0, as well as the set of points for which −2 + X1 + 2X2 < 0.
- We have seen that in p = 2 dimensions, a linear decision boundary takes the form β0+β1X1+β2X2 = 0. We now investigate a non-linear decision boundary.
- Sketch the curve
\[(1+X\_1)^2 + (2-X\_2)^2 = 4.\]
- On your sketch, indicate the set of points for which
\[(1+X\_1)^2 + (2-X\_2)^2 > 4,\]
as well as the set of points for which
\[(1+X\_1)^2 + (2-X\_2)^2 \le 4.\]
- Suppose that a classifer assigns an observation to the blue class if
\[(1+X\_1)^2+(2-X\_2)^2>4,\]
and to the red class otherwise. To what class is the observation (0, 0) classifed? (−1, 1)? (2, 2)? (3, 8)?
- Argue that while the decision boundary in (c) is not linear in terms of X1 and X2, it is linear in terms of X1, X2 1 , X2, and X2 2 .
- Here we explore the maximal margin classifer on a toy data set.
| Obs. | X1 | X2 | Y |
|---|---|---|---|
| 1 | 3 | 4 | Red |
| 2 | 2 | 2 | Red |
| 3 | 4 | 4 | Red |
| 4 | 1 | 4 | Red |
| 5 | 2 | 1 | Blue |
| 6 | 4 | 3 | Blue |
| 7 | 4 | 1 | Blue |
- We are given n = 7 observations in p = 2 dimensions. For each observation, there is an associated class label.
Sketch the observations.
- Sketch the optimal separating hyperplane, and provide the equation for this hyperplane (of the form (9.1)).
- Describe the classifcation rule for the maximal margin classifer. It should be something along the lines of “Classify to Red if β0 + β1X1 + β2X2 > 0, and classify to Blue otherwise.” Provide the values for β0, β1, and β2.
- On your sketch, indicate the margin for the maximal margin hyperplane.
- Indicate the support vectors for the maximal margin classifer.
- Argue that a slight movement of the seventh observation would not afect the maximal margin hyperplane.
- Sketch a hyperplane that is not the optimal separating hyperplane, and provide the equation for this hyperplane.
- Draw an additional observation on the plot so that the two classes are no longer separable by a hyperplane.
Applied
- Generate a simulated two-class data set with 100 observations and two features in which there is a visible but non-linear separation between the two classes. Show that in this setting, a support vector machine with a polynomial kernel (with degree greater than 1) or a radial kernel will outperform a support vector classifer on the training data. Which technique performs best on the test data? Make plots and report training and test error rates in order to back up your assertions.
- We have seen that we can ft an SVM with a non-linear kernel in order to perform classifcation using a non-linear decision boundary. We will now see that we can also obtain a non-linear decision boundary by performing logistic regression using non-linear transformations of the features.
- Generate a data set with n = 500 and p = 2, such that the observations belong to two classes with a quadratic decision boundary between them. For instance, you can do this as follows:
rng = np.random.default_rng(5)
x1 = rng.uniform(size=500) - 0.5
x2 = rng.uniform(size=500) - 0.5
y = x1**2 - x2**2 > 0- Plot the observations, colored according to their class labels. Your plot should display X1 on the x-axis, and X2 on the yaxis.
- Fit a logistic regression model to the data, using X1 and X2 as predictors.
- Apply this model to the training data in order to obtain a predicted class label for each training observation. Plot the observations, colored according to the predicted class labels. The decision boundary should be linear.
- Now ft a logistic regression model to the data using non-linear functions of X1 and X2 as predictors (e.g. X2 1 , X1×X2, log(X2), and so forth).
- Apply this model to the training data in order to obtain a predicted class label for each training observation. Plot the observations, colored according to the predicted class labels. The decision boundary should be obviously non-linear. If it is not, then repeat (a)–(e) until you come up with an example in which the predicted class labels are obviously non-linear.
- Fit a support vector classifer to the data with X1 and X2 as predictors. Obtain a class prediction for each training observation. Plot the observations, colored according to the predicted class labels.
- Fit a SVM using a non-linear kernel to the data. Obtain a class prediction for each training observation. Plot the observations, colored according to the predicted class labels.
- Comment on your results.
- At the end of Section 9.6.1, it is claimed that in the case of data that is just barely linearly separable, a support vector classifer with a small value of C that misclassifes a couple of training observations may perform better on test data than one with a huge value of C that does not misclassify any training observations. You will now investigate this claim.
- Generate two-class data with p = 2 in such a way that the classes are just barely linearly separable.
- Compute the cross-validation error rates for support vector classifers with a range of C values. How many training observations are misclassifed for each value of C considered, and how does this relate to the cross-validation errors obtained?
- Generate an appropriate test data set, and compute the test errors corresponding to each of the values of C considered. Which value of C leads to the fewest test errors, and how does this compare to the values of C that yield the fewest training errors and the fewest cross-validation errors?
- Discuss your results.
- In this problem, you will use support vector approaches in order to predict whether a given car gets high or low gas mileage based on the Auto data set.
- Create a binary variable that takes on a 1 for cars with gas mileage above the median, and a 0 for cars with gas mileage below the median.
- Fit a support vector classifer to the data with various values of C, in order to predict whether a car gets high or low gas mileage. Report the cross-validation errors associated with diferent values of this parameter. Comment on your results. Note you will need to ft the classifer without the gas mileage variable to produce sensible results.
- Now repeat (b), this time using SVMs with radial and polynomial basis kernels, with diferent values of gamma and degree and C. Comment on your results.
- Make some plots to back up your assertions in (b) and (c).
Hint: In the lab, we used the plot_svm() function for ftted SVMs. When p > 2, you can use the keyword argument features to create plots displaying pairs of variables at a time.
- This problem involves the OJ data set which is part of the ISLP package.
- Create a training set containing a random sample of 800 observations, and a test set containing the remaining observations.
- Fit a support vector classifer to the training data using C = 0.01, with Purchase as the response and the other variables as predictors. How many support points are there?
- What are the training and test error rates?
- Use cross-validation to select an optimal C. Consider values in the range 0.01 to 10.
- Compute the training and test error rates using this new value for C.
- Repeat parts (b) through (e) using a support vector machine with a radial kernel. Use the default value for gamma.
- Repeat parts (b) through (e) using a support vector machine with a polynomial kernel. Set degree = 2.
- Overall, which approach seems to give the best results on this data?
10 Deep Learning

This chapter covers the important topic of deep learning. At the time of deep writing (2020), deep learning is a very active area of research in the machine learning learning and artifcial intelligence communities. The cornerstone of deep
learning is the neural network. neural Neural networks rose to fame in the late 1980s. There was a lot of excite- network ment and a certain amount of hype associated with this approach, and they were the impetus for the popular Neural Information Processing Systems meetings (NeurIPS, formerly NIPS) held every year, typically in exotic places like ski resorts. This was followed by a synthesis stage, where the properties of neural networks were analyzed by machine learners, mathematicians and statisticians; algorithms were improved, and the methodology stabilized. Then along came SVMs, boosting, and random forests, and neural networks fell somewhat from favor. Part of the reason was that neural networks required a lot of tinkering, while the new methods were more automatic. Also, on many problems the new methods outperformed poorly-trained neural networks. This was the status quo for the frst decade in the new millennium.
All the while, though, a core group of neural-network enthusiasts were pushing their technology harder on ever-larger computing architectures and data sets. Neural networks resurfaced after 2010 with the new name deep learning, with new architectures, additional bells and whistles, and a string of success stories on some niche problems such as image and video classifcation, speech and text modeling. Many in the feld believe that the major reason for these successes is the availability of ever-larger training datasets, made possible by the wide-scale use of digitization in science and industry.
In this chapter we discuss the basics of neural networks and deep learning, and then go into some of the specializations for specifc problems, such as convolutional neural networks (CNNs) for image classifcation, and recurrent neural networks (RNNs) for time series and other sequences. We
© Springer Nature Switzerland AG 2023
G. James et al., An Introduction to Statistical Learning, Springer Texts in Statistics, https://doi.org/10.1007/978-3-031-38747-0\_10
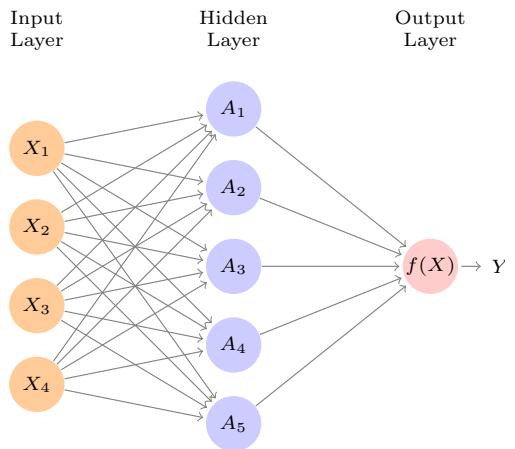
FIGURE 10.1. Neural network with a single hidden layer. The hidden layer computes activations Ak = hk(X) that are nonlinear transformations of linear combinations of the inputs X1, X2,…,Xp. Hence these Ak are not directly observed. The functions hk(·) are not fxed in advance, but are learned during the training of the network. The output layer is a linear model that uses these activations Ak as inputs, resulting in a function f(X).
will also demonstrate these models using the Python torch package, along with a number of helper packages.
The material in this chapter is slightly more challenging than elsewhere in this book.
10.1 Single Layer Neural Networks
A neural network takes an input vector of p variables X = (X1, X2,…,Xp) and builds a nonlinear function f(X) to predict the response Y . We have built nonlinear prediction models in earlier chapters, using trees, boosting and generalized additive models. What distinguishes neural networks from these methods is the particular structure of the model. Figure 10.1 shows a simple feed-forward neural network for modeling a quantitative response feed-forward using p = 4 predictors. In the terminology of neural networks, the four features X1,…,X4 make up the units in the input layer. The arrows indicate that each of the inputs from the input layer feeds into each of the K hidden input layer units (we get to pick K; here we chose 5). The neural network model has hidden units the form
neural network
\[\begin{aligned} f(X) &= \beta\_0 + \sum\_{k=1}^{K} \beta\_k h\_k(X) \\ &= \beta\_0 + \sum\_{k=1}^{K} \beta\_k g(w\_{k0} + \sum\_{j=1}^{p} w\_{kj} X\_j). \end{aligned} \tag{10.1}\]
It is built up here in two steps. First the K activations Ak, k = 1, . . . , K, in activations the hidden layer are computed as functions of the input features X1,…,Xp,
\[A\_k = h\_k(X) = g(w\_{k0} + \sum\_{j=1}^p w\_{kj} X\_j),\tag{10.2}\]
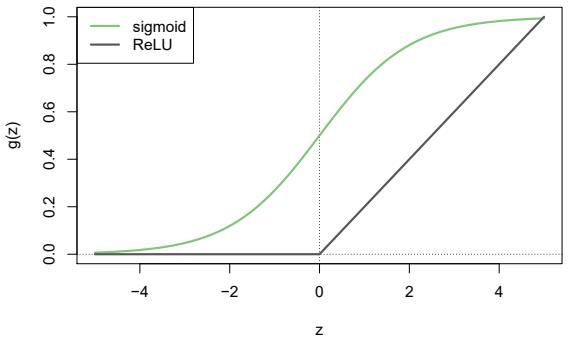
FIGURE 10.2. Activation functions. The piecewise-linear ReLU function is popular for its efciency and computability. We have scaled it down by a factor of fve for ease of comparison.
where g(z) is a nonlinear activation function that is specifed in advance. activation We can think of each Ak function as a diferent transformation hk(X) of the original features, much like the basis functions of Chapter 7. These K activations from the hidden layer then feed into the output layer, resulting in
\[f(X) = \beta\_0 + \sum\_{k=1}^{K} \beta\_k A\_k,\tag{10.3}\]
a linear regression model in the K = 5 activations. All the parameters β0,…, βK and w10,…,wKp need to be estimated from data. In the early instances of neural networks, the sigmoid activation function was favored, sigmoid
\[g(z) = \frac{e^z}{1 + e^z} = \frac{1}{1 + e^{-z}},\tag{10.4}\]
which is the same function used in logistic regression to convert a linear function into probabilities between zero and one (see Figure 10.2). The preferred choice in modern neural networks is the ReLU (rectifed linear ReLU unit) activation function, which takes the form rectifed
linear unit
\[g(z) = (z)\_{+} = \begin{cases} 0 & \text{if } z < 0\\ \, \, z & \text{otherwise.} \end{cases} \tag{10.5}\]
A ReLU activation can be computed and stored more efciently than a sigmoid activation. Although it thresholds at zero, because we apply it to a linear function (10.2) the constant term wk0 will shift this infection point.
So in words, the model depicted in Figure 10.1 derives fve new features by computing fve diferent linear combinations of X, and then squashes each through an activation function g(·) to transform it. The fnal model is linear in these derived variables.
The name neural network originally derived from thinking of these hidden units as analogous to neurons in the brain — values of the activations Ak = hk(X) close to one are fring, while those close to zero are silent (using the sigmoid activation function).
The nonlinearity in the activation function g(·) is essential, since without it the model f(X) in (10.1) would collapse into a simple linear model in X1,…,Xp. Moreover, having a nonlinear activation function allows the model to capture complex nonlinearities and interaction efects. Consider a very simple example with p = 2 input variables X = (X1, X2), and K = 2 hidden units h1(X) and h2(X) with g(z) = z2. We specify the other parameters as
\[\begin{array}{ll} \beta\_0 = 0, & \beta\_1 = \frac{1}{4}, \quad \beta\_2 = -\frac{1}{4}, \\ w\_{10} = 0, & w\_{11} = 1, \quad w\_{12} = 1, \\ w\_{20} = 0, & w\_{21} = 1, \quad w\_{22} = -1. \end{array} \tag{10.6}\]
From (10.2), this means that
\[\begin{array}{rcl} h\_1(X) &=& (0 + X\_1 + X\_2)^2, \\ h\_2(X) &=& (0 + X\_1 - X\_2)^2. \end{array} \tag{10.7}\]
Then plugging (10.7) into (10.1), we get
\[\begin{array}{rcl} f(X) &=& 0 + \frac{1}{4} \cdot (0 + X\_1 + X\_2)^2 - \frac{1}{4} \cdot (0 + X\_1 - X\_2)^2 \\ &=& \frac{1}{4} \left[ (X\_1 + X\_2)^2 - (X\_1 - X\_2)^2 \right] \\ &=& X\_1 X\_2. \end{array} \tag{10.8}\]
So the sum of two nonlinear transformations of linear functions can give us an interaction! In practice we would not use a quadratic function for g(z), since we would always get a second-degree polynomial in the original coordinates X1,…,Xp. The sigmoid or ReLU activations do not have such a limitation.
Fitting a neural network requires estimating the unknown parameters in (10.1). For a quantitative response, typically squared-error loss is used, so that the parameters are chosen to minimize
\[\sum\_{i=1}^{n} \left( y\_i - f(x\_i) \right)^2. \tag{10.9}\]
Details about how to perform this minimization are provided in Section 10.7.
10.2 Multilayer Neural Networks
Modern neural networks typically have more than one hidden layer, and often many units per layer. In theory a single hidden layer with a large number of units has the ability to approximate most functions. However, the learning task of discovering a good solution is made much easier with multiple layers each of modest size.
We will illustrate a large dense network on the famous and publicly available MNIST handwritten digit dataset.1 Figure 10.3 shows examples of these digits. The idea is to build a model to classify the images into their correct digit class 0–9. Every image has p = 28 × 28 = 784 pixels, each of which is an eight-bit grayscale value between 0 and 255 representing
1See LeCun, Cortes, and Burges (2010) “The MNIST database of handwritten digits”, available at http://yann.lecun.com/exdb/mnist.
FIGURE 10.3. Examples of handwritten digits from the MNIST corpus. Each grayscale image has 28 × 28 pixels, each of which is an eight-bit number (0–255) which represents how dark that pixel is. The frst 3, 5, and 8 are enlarged to show their 784 individual pixel values.
the relative amount of the written digit in that tiny square.2 These pixels are stored in the input vector X (in, say, column order). The output is the class label, represented by a vector Y = (Y0, Y1,…,Y9) of 10 dummy variables, with a one in the position corresponding to the label, and zeros elsewhere. In the machine learning community, this is known as one-hot
encoding. There are 60,000 training images, and 10,000 test images. one-hot On a historical note, digit recognition problems were the catalyst that encoding accelerated the development of neural network technology in the late 1980s at AT&T Bell Laboratories and elsewhere. Pattern recognition tasks of this kind are relatively simple for humans. Our visual system occupies a large fraction of our brains, and good recognition is an evolutionary force for survival. These tasks are not so simple for machines, and it has taken more than 30 years to refne the neural-network architectures to match human performance.
Figure 10.4 shows a multilayer network architecture that works well for solving the digit-classifcation task. It difers from Figure 10.1 in several ways:
- It has two hidden layers L1 (256 units) and L2 (128 units) rather than one. Later we will see a network with seven hidden layers.
- It has ten output variables, rather than one. In this case the ten variables really represent a single qualitative variable and so are quite dependent. (We have indexed them by the digit class 0–9 rather than 1–10, for clarity.) More generally, in multi-task learning one can pre- multi-task learning dict diferent responses simultaneously with a single network; they all have a say in the formation of the hidden layers.
- The loss function used for training the network is tailored for the multiclass classifcation task.
2In the analog-to-digital conversion process, only part of the written numeral may fall in the square representing a particular pixel.
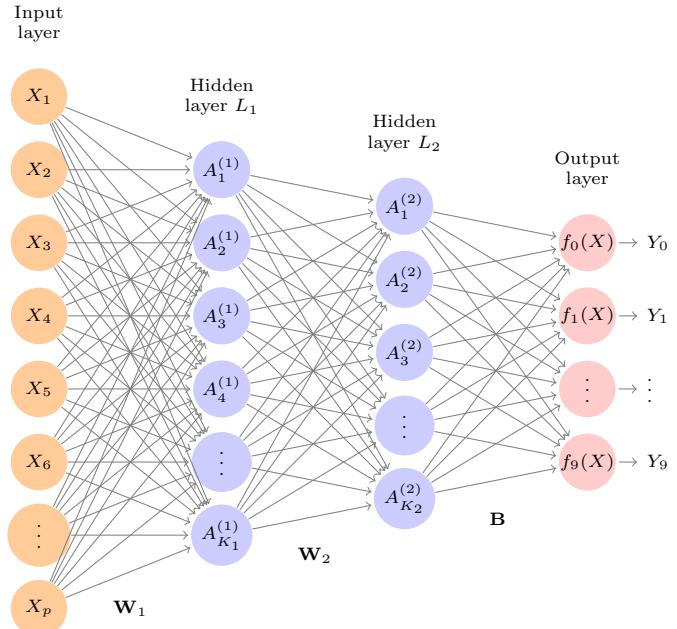
FIGURE 10.4. Neural network diagram with two hidden layers and multiple outputs, suitable for the MNIST handwritten-digit problem. The input layer has p = 784 units, the two hidden layers K1 = 256 and K2 = 128 units respectively, and the output layer 10 units. Along with intercepts (referred to as biases in the deep-learning community) this network has 235,146 parameters (referred to as weights).
The frst hidden layer is as in (10.2), with
\[\begin{array}{rcl} A\_k^{(1)} &=& h\_k^{(1)}(X) \\ &=& g(w\_{k0}^{(1)} + \sum\_{j=1}^p w\_{kj}^{(1)} X\_j) \end{array} \tag{10.10}\]
for k = 1,…,K1. The second hidden layer treats the activations A(1) k of the frst hidden layer as inputs and computes new activations
\[\begin{array}{rcl} A\_{\ell}^{(2)} & = & h\_{\ell}^{(2)}(X) \\ & = & g(w\_{\ell 0}^{(2)} + \sum\_{k=1}^{K\_1} w\_{\ell k}^{(2)} A\_k^{(1)}) \end{array} \tag{10.11}\]
for ℓ = 1,…,K2. Notice that each of the activations in the second layer A(2) ℓ = h(2) ℓ (X) is a function of the input vector X. This is the case because while they are explicitly a function of the activations A(1) k from layer L1, these in turn are functions of X. This would also be the case with more hidden layers. Thus, through a chain of transformations, the network is able to build up fairly complex transformations of X that ultimately feed into the output layer as features.
We have introduced additional superscript notation such as h(2) ℓ (X) and w(2) ℓj in (10.10) and (10.11) to indicate to which layer the activations and weights (coefcients) belong, in this case layer 2. The notation W1 in Fig- weights ure 10.4 represents the entire matrix of weights that feed from the input layer to the frst hidden layer L1. This matrix will have 785×256 = 200,960 elements; there are 785 rather than 784 because we must account for the intercept or bias term.3
Each element A(1) k feeds to the second hidden layer L2 via the matrix of weights W2 of dimension 257 × 128 = 32,896.
We now get to the output layer, where we now have ten responses rather than one. The frst step is to compute ten diferent linear models similar to our single model (10.1),
\[\begin{aligned} Z\_m &= \ \beta\_{m0} + \sum\_{\ell=1}^{K\_2} \beta\_{m\ell} h\_{\ell}^{(2)}(X) \\ &= \ \beta\_{m0} + \sum\_{\ell=1}^{K\_2} \beta\_{m\ell} A\_{\ell}^{(2)}, \end{aligned} \tag{10.12}\]
for m = 0, 1,…, 9. The matrix B stores all 129 × 10 = 1,290 of these weights.
If these were all separate quantitative responses, we would simply set each fm(X) = Zm and be done. However, we would like our estimates to represent class probabilities fm(X) = Pr(Y = m|X), just like in multinomial logistic regression in Section 4.3.5. So we use the special softmax softmax activation function (see (4.13) on page 145),
\[f\_m(X) = \Pr(Y = m | X) = \frac{e^{Z\_m}}{\sum\_{\ell=0}^9 e^{Z\_\ell}},\tag{10.13}\]
for m = 0, 1,…, 9. This ensures that the 10 numbers behave like probabilities (non-negative and sum to one). Even though the goal is to build a classifer, our model actually estimates a probability for each of the 10 classes. The classifer then assigns the image to the class with the highest probability.
To train this network, since the response is qualitative, we look for coeffcient estimates that minimize the negative multinomial log-likelihood
\[-\sum\_{i=1}^{n}\sum\_{m=0}^{9}y\_{im}\log(f\_m(x\_i)),\tag{10.14}\]
also known as the cross-entropy. This is a generalization of the crite- crossrion (4.5) for two-class logistic regression. Details on how to minimize this entropy objective are given in Section 10.7. If the response were quantitative, we would instead minimize squared-error loss as in (10.9).
Table 10.1 compares the test performance of the neural network with two simple models presented in Chapter 4 that make use of linear decision boundaries: multinomial logistic regression and linear discriminant analysis. The improvement of neural networks over both of these linear methods is dramatic: the network with dropout regularization achieves a test error rate below 2% on the 10,000 test images. (We describe dropout regularization in Section 10.7.3.) In Section 10.9.2 of the lab, we present the code for ftting this model, which runs in just over two minutes on a laptop computer.
bias
3The use of “weights” for coefcients and “bias” for the intercepts wk0 in (10.2) is popular in the machine learning community; this use of bias is not to be confused with the “bias-variance” usage elsewhere in this book.
406 10. Deep Learning
| Method | Test Error |
|---|---|
| Neural Network + Ridge Regularization | 2.3% |
| Neural Network + Dropout Regularization | 1.8% |
| Multinomial Logistic Regression | 7.2% |
| Linear Discriminant Analysis | 12.7% |
TABLE 10.1. Test error rate on the MNIST data, for neural networks with two forms of regularization, as well as multinomial logistic regression and linear discriminant analysis. In this example, the extra complexity of the neural network leads to a marked improvement in test error.

FIGURE 10.5. A sample of images from the CIFAR100 database: a collection of natural images from everyday life, with 100 diferent classes represented.
Adding the number of coefcients in W1, W2 and B, we get 235,146 in all, more than 33 times the number 785×9=7,065 needed for multinomial logistic regression. Recall that there are 60,000 images in the training set. While this might seem like a large training set, there are almost four times as many coefcients in the neural network model as there are observations in the training set! To avoid overftting, some regularization is needed. In this example, we used two forms of regularization: ridge regularization, which is similar to ridge regression from Chapter 6, and dropout regularization. dropout We discuss both forms of regularization in Section 10.7.
10.3 Convolutional Neural Networks
Neural networks rebounded around 2010 with big successes in image classifcation. Around that time, massive databases of labeled images were being accumulated, with ever-increasing numbers of classes. Figure 10.5 shows 75 images drawn from the CIFAR100 database.4 This database consists of 60,000 images labeled according to 20 superclasses (e.g. aquatic mammals), with fve classes per superclass (beaver, dolphin, otter, seal, whale). Each image has a resolution of 32 × 32 pixels, with three eight-bit numbers per pixel representing red, green and blue. The numbers for each image are organized in a three-dimensional array called a feature map. The frst two feature map
4See Chapter 3 of Krizhevsky (2009) “Learning multiple layers of features from tiny images”, available at https://www.cs.toronto.edu/~kriz/ learning-features-2009-TR.pdf.
FIGURE 10.6. Schematic showing how a convolutional neural network classifes an image of a tiger. The network takes in the image and identifes local features. It then combines the local features in order to create compound features, which in this example include eyes and ears. These compound features are used to output the label “tiger”.
axes are spatial (both are 32-dimensional), and the third is the channel channel axis,5 representing the three colors. There is a designated training set of 50,000 images, and a test set of 10,000.
A special family of convolutional neural networks (CNNs) has evolved for convolutional classifying images such as these, and has shown spectacular success on a wide range of problems. CNNs mimic to some degree how humans classify images, by recognizing specifc features or patterns anywhere in the image that distinguish each particular object class. In this section we give a brief overview of how they work.
Figure 10.6 illustrates the idea behind a convolutional neural network on a cartoon image of a tiger.6
The network frst identifes low-level features in the input image, such as small edges, patches of color, and the like. These low-level features are then combined to form higher-level features, such as parts of ears, eyes, and so on. Eventually, the presence or absence of these higher-level features contributes to the probability of any given output class.
How does a convolutional neural network build up this hierarchy? It combines two specialized types of hidden layers, called convolution layers and pooling layers. Convolution layers search for instances of small patterns in the image, whereas pooling layers downsample these to select a prominent subset. In order to achieve state-of-the-art results, contemporary neuralnetwork architectures make use of many convolution and pooling layers. We describe convolution and pooling layers next.
10.3.1 Convolution Layers
A convolution layer is made up of a large number of convolution flters, each convolution
layer convolution flter
neural networks
5The term channel is taken from the signal-processing literature. Each channel is a distinct source of information.
6 Thanks to Elena Tuzhilina for producing the diagram and https://www. cartooning4kids.com/ for permission to use the cartoon tiger.
of which is a template that determines whether a particular local feature is present in an image. A convolution flter relies on a very simple operation, called a convolution, which basically amounts to repeatedly multiplying matrix elements and then adding the results.
To understand how a convolution flter works, consider a very simple example of a 4 × 3 image:
\[ \text{Original Image} = \begin{bmatrix} a & b & c \\ d & e & f \\ g & h & i \\ j & k & l \end{bmatrix}. \]
Now consider a 2 × 2 flter of the form
\[\text{Convolution Filter} = \begin{bmatrix} \alpha & \beta \\ \gamma & \delta \end{bmatrix}.\]
When we convolve the image with the flter, we get the result7
\[\text{Convolved Image} = \begin{bmatrix} a\alpha + b\beta + d\gamma + e\delta & b\alpha + c\beta + e\gamma + f\delta \\ d\alpha + e\beta + g\gamma + h\delta & e\alpha + f\beta + h\gamma + i\delta \\ g\alpha + h\beta + j\gamma + k\delta & h\alpha + i\beta + k\gamma + l\delta \end{bmatrix}.\]
For instance, the top-left element comes from multiplying each element in the 2 × 2 flter by the corresponding element in the top left 2 × 2 portion of the image, and adding the results. The other elements are obtained in a similar way: the convolution flter is applied to every 2×2 submatrix of the original image in order to obtain the convolved image. If a 2 × 2 submatrix of the original image resembles the convolution flter, then it will have a large value in the convolved image; otherwise, it will have a small value. Thus, the convolved image highlights regions of the original image that resemble the convolution flter. We have used 2 × 2 as an example; in general convolution flters are small ℓ1 × ℓ2 arrays, with ℓ1 and ℓ2 small positive integers that are not necessarily equal.
Figure 10.7 illustrates the application of two convolution flters to a 192× 179 image of a tiger, shown on the left-hand side.8 Each convolution flter is a 15 × 15 image containing mostly zeros (black), with a narrow strip of ones (white) oriented either vertically or horizontally within the image. When each flter is convolved with the image of the tiger, areas of the tiger that resemble the flter (i.e. that have either horizontal or vertical stripes or edges) are given large values, and areas of the tiger that do not resemble the feature are given small values. The convolved images are displayed on the right-hand side. We see that the horizontal stripe flter picks out horizontal stripes and edges in the original image, whereas the vertical stripe flter picks out vertical stripes and edges in the original image.
7The convolved image is smaller than the original image because its dimension is given by the number of 2 × 2 submatrices in the original image. Note that 2 × 2 is the dimension of the convolution flter. If we want the convolved image to have the same dimension as the original image, then padding can be applied.
8The tiger image used in Figures 10.7–10.9 was obtained from the public domain image resource https://www.needpix.com/.

FIGURE 10.7. Convolution flters fnd local features in an image, such as edges and small shapes. We begin with the image of the tiger shown on the left, and apply the two small convolution flters in the middle. The convolved images highlight areas in the original image where details similar to the flters are found. Specifcally, the top convolved image highlights the tiger’s vertical stripes, whereas the bottom convolved image highlights the tiger’s horizontal stripes. We can think of the original image as the input layer in a convolutional neural network, and the convolved images as the units in the frst hidden layer.
We have used a large image and two large flters in Figure 10.7 for illustration. For the CIFAR100 database there are 32×32 color pixels per image, and we use 3 × 3 convolution flters.
In a convolution layer, we use a whole bank of flters to pick out a variety of diferently-oriented edges and shapes in the image. Using predefned flters in this way is standard practice in image processing. By contrast, with CNNs the flters are learned for the specifc classifcation task. We can think of the flter weights as the parameters going from an input layer to a hidden layer, with one hidden unit for each pixel in the convolved image. This is in fact the case, though the parameters are highly structured and constrained (see Exercise 4 for more details). They operate on localized patches in the input image (so there are many structural zeros), and the same weights in a given flter are reused for all possible patches in the image (so the weights are constrained).9
We now give some additional details.
• Since the input image is in color, it has three channels represented by a three-dimensional feature map (array). Each channel is a twodimensional (32 × 32) feature map — one for red, one for green, and one for blue. A single convolution flter will also have three channels, one per color, each of dimension 3×3, with potentially diferent flter weights. The results of the three convolutions are summed to form a two-dimensional output feature map. Note that at this point the color information has been used, and is not passed on to subsequent layers except through its role in the convolution.
9This used to be called weight sharing in the early years of neural networks.
410 10. Deep Learning
- If we use K diferent convolution flters at this frst hidden layer, we get K two-dimensional output feature maps, which together are treated as a single three-dimensional feature map. We view each of the K output feature maps as a separate channel of information, so now we have K channels in contrast to the three color channels of the original input feature map. The three-dimensional feature map is just like the activations in a hidden layer of a simple neural network, except organized and produced in a spatially structured way.
- We typically apply the ReLU activation function (10.5) to the convolved image. This step is sometimes viewed as a separate layer in the convolutional neural network, in which case it is referred to as a detector layer. detector
layer
10.3.2 Pooling Layers
A pooling layer provides a way to condense a large image into a smaller pooling summary image. While there are a number of possible ways to perform pooling, the max pooling operation summarizes each non-overlapping 2 × 2 block of pixels in an image using the maximum value in the block. This reduces the size of the image by a factor of two in each direction, and it also provides some location invariance: i.e. as long as there is a large value in one of the four pixels in the block, the whole block registers as a large value in the reduced image.
Here is a simple example of max pooling:
Max pool ⎡ ⎢ ⎢ ⎣ 1253 3012 2134 1120 ⎤ ⎥ ⎥ ⎦ → ’ 3 5 2 4( .
10.3.3 Architecture of a Convolutional Neural Network
So far we have defned a single convolution layer — each flter produces a new two-dimensional feature map. The number of convolution flters in a convolution layer is akin to the number of units at a particular hidden layer in a fully-connected neural network of the type we saw in Section 10.2. This number also defnes the number of channels in the resulting threedimensional feature map. We have also described a pooling layer, which reduces the frst two dimensions of each three-dimensional feature map. Deep CNNs have many such layers. Figure 10.8 shows a typical architecture for a CNN for the CIFAR100 image classifcation task.
At the input layer, we see the three-dimensional feature map of a color image, where the channel axis represents each color by a 32 × 32 twodimensional feature map of pixels. Each convolution flter produces a new channel at the frst hidden layer, each of which is a 32 × 32 feature map (after some padding at the edges). After this frst round of convolutions, we now have a new “image”; a feature map with considerably more channels than the three color input channels (six in the fgure, since we used six convolution flters).
FIGURE 10.8. Architecture of a deep CNN for the CIFAR100 classifcation task. Convolution layers are interspersed with 2 × 2 max-pool layers, which reduce the size by a factor of 2 in both dimensions.
This is followed by a max-pool layer, which reduces the size of the feature map in each channel by a factor of four: two in each dimension.
This convolve-then-pool sequence is now repeated for the next two layers. Some details are as follows:
- Each subsequent convolve layer is similar to the frst. It takes as input the three-dimensional feature map from the previous layer and treats it like a single multi-channel image. Each convolution flter learned has as many channels as this feature map.
- Since the channel feature maps are reduced in size after each pool layer, we usually increase the number of flters in the next convolve layer to compensate.
- Sometimes we repeat several convolve layers before a pool layer. This efectively increases the dimension of the flter.
These operations are repeated until the pooling has reduced each channel feature map down to just a few pixels in each dimension. At this point the three-dimensional feature maps are fattened — the pixels are treated as separate units — and fed into one or more fully-connected layers before reaching the output layer, which is a softmax activation for the 100 classes (as in (10.13)).
There are many tuning parameters to be selected in constructing such a network, apart from the number, nature, and sizes of each layer. Dropout learning can be used at each layer, as well as lasso or ridge regularization (see Section 10.7). The details of constructing a convolutional neural network can seem daunting. Fortunately, terrifc software is available, with extensive examples and vignettes that provide guidance on sensible choices for the parameters. For the CIFAR100 ofcial test set, the best accuracy as of this writing is just above 75%, but undoubtedly this performance will continue to improve.
10.3.4 Data Augmentation
An additional important trick used with image modeling is data augment- data augmentation ation. Essentially, each training image is replicated many times, with each replicate randomly distorted in a natural way such that human recognition is unafected. Figure 10.9 shows some examples. Typical distortions are

FIGURE 10.9. Data augmentation. The original image (leftmost) is distorted in natural ways to produce diferent images with the same class label. These distortions do not fool humans, and act as a form of regularization when ftting the CNN.
zoom, horizontal and vertical shift, shear, small rotations, and in this case horizontal fips. At face value this is a way of increasing the training set considerably with somewhat diferent examples, and thus protects against overftting. In fact we can see this as a form of regularization: we build a cloud of images around each original image, all with the same label. This kind of fattening of the data is similar in spirit to ridge regularization.
We will see in Section 10.7.2 that the stochastic gradient descent algorithms for ftting deep learning models repeatedly process randomlyselected batches of, say, 128 training images at a time. This works hand-inglove with augmentation, because we can distort each image in the batch on the fy, and hence do not have to store all the new images.
10.3.5 Results Using a Pretrained Classifer
Here we use an industry-level pretrained classifer to predict the class of some new images. The resnet50 classifer is a convolutional neural network that was trained using the imagenet data set, which consists of millions of images that belong to an ever-growing number of categories.10 Figure 10.10 demonstrates the performance of resnet50 on six photographs (private collection of one of the authors).11 The CNN does a reasonable job classifying the hawk in the second image. If we zoom out as in the third image, it gets confused and chooses the fountain rather than the hawk. In the fnal image a “jacamar” is a tropical bird from South and Central America with similar coloring to the South African Cape Weaver. We give more details on this example in Section 10.9.4.
Much of the work in ftting a CNN is in learning the convolution flters at the hidden layers; these are the coefcients of a CNN. For models ft to massive corpora such as imagenet with many classes, the output of these flters can serve as features for general natural-image classifcation problems. One can use these pretrained hidden layers for new problems with much smaller training sets (a process referred to as weight freezing), and weight freezing just train the last few layers of the network, which requires much less data.
10For more information about resnet50, see He, Zhang, Ren, and Sun (2015) “Deep residual learning for image recognition”, https://arxiv.org/abs/1512.03385. For details about imagenet, see Russakovsky, Deng, et al. (2015) “ImageNet Large Scale Visual Recognition Challenge”, in International Journal of Computer Vision.
11These resnet results can change with time, since the publicly-trained model gets updated periodically.
| famingo famingo |
0.83 | Cooper’s hawk kite |
0.60 | Cooper’s hawk fountain |
0.35 |
|---|---|---|---|---|---|
| spoonbill | 0.17 | great grey owl | 0.09 | nail | 0.12 |
| white stork | 0.00 | robin | 0.06 | hook | 0.07 |
| Lhasa Apso | cat | Cape weaver | |||
| Tibetan terrier | 0.56 | Old English sheepdog | 0.82 | jacamar | 0.28 |
| Lhasa | 0.32 | Shih-Tzu | 0.04 | macaw | 0.12 |
| cocker spaniel | 0.03 | Persian cat | 0.04 | robin | 0.12 |
FIGURE 10.10. Classifcation of six photographs using the resnet50 CNN trained on the imagenet corpus. The table below the images displays the true (intended) label at the top of each panel, and the top three choices of the classifer (out of 100). The numbers are the estimated probabilities for each choice. (A kite is a raptor, but not a hawk.)
The vignettes and book12 that accompany the keras package give more details on such applications.
10.4 Document Classifcation
In this section we introduce a new type of example that has important applications in industry and science: predicting attributes of documents. Examples of documents include articles in medical journals, Reuters news feeds, emails, tweets, and so on. Our example will be IMDb (Internet Movie Database) ratings — short documents where viewers have written critiques of movies.13 The response in this case is the sentiment of the review, which will be positive or negative.
12Deep Learning with R by F. Chollet and J.J. Allaire, 2018, Manning Publications.
13For details, see Maas et al. (2011) “Learning word vectors for sentiment analysis”, in Proceedings of the 49th Annual Meeting of the Association for Computational Linguistics: Human Language Technologies, pages 142–150.
Here is the beginning of a rather amusing negative review:
This has to be one of the worst flms of the 1990s. When my friends & I were watching this flm (being the target audience it was aimed at) we just sat & watched the frst half an hour with our jaws touching the foor at how bad it really was. The rest of the time, everyone else in the theater just started talking to each other, leaving or generally crying into their popcorn …
Each review can be a diferent length, include slang or non-words, have spelling errors, etc. We need to fnd a way to featurize such a document. featurize This is modern parlance for defning a set of predictors.
The simplest and most common featurization is the bag-of-words model. bag-of-words We score each document for the presence or absence of each of the words in a language dictionary — in this case an English dictionary. If the dictionary contains M words, that means for each document we create a binary feature vector of length M, and score a 1 for every word present, and 0 otherwise. That can be a very wide feature vector, so we limit the dictionary — in this case to the 10,000 most frequently occurring words in the training corpus of 25,000 reviews. Fortunately there are nice tools for doing this automatically. Here is the beginning of a positive review that has been redacted in this way:
⟨START ⟩ this flm was just brilliant casting location scenery story direction everyone’s really suited the part they played and you could just imagine being there robert ⟨UNK ⟩ is an amazing actor and now the same being director ⟨UNK ⟩ father came from the same scottish island as myself so i loved …
Here we can see many words have been omitted, and some unknown words (UNK) have been marked as such. With this reduction the binary feature vector has length 10,000, and consists mostly of 0’s and a smattering of 1’s in the positions corresponding to words that are present in the document. We have a training set and test set, each with 25,000 examples, and each balanced with regard to sentiment. The resulting training feature matrix X has dimension 25,000×10,000, but only 1.3% of the binary entries are nonzero. We call such a matrix sparse, because most of the values are the same (zero in this case); it can be stored efciently in sparse matrix format. 14 There are a variety of ways to account for the document length; here we only score a word as in or out of the document, but for example one could instead record the relative frequency of words. We split of a validation set of size 2,000 from the 25,000 training observations (for model tuning), and ft two model sequences:
sparse matrix format
- A lasso logistic regression using the glmnet package;
- A two-class neural network with two hidden layers, each with 16 ReLU units.
14Rather than store the whole matrix, we can store instead the location and values for the nonzero entries. In this case, since the nonzero entries are all 1, just the locations are stored.
FIGURE 10.11. Accuracy of the lasso and a two-hidden-layer neural network on the IMDb data. For the lasso, the x-axis displays − log(λ), while for the neural network it displays epochs (number of times the ftting algorithm passes through the training set). Both show a tendency to overft, and achieve approximately the same test accuracy.
Both methods produce a sequence of solutions. The lasso sequence is indexed by the regularization parameter λ. The neural-net sequence is indexed by the number of gradient-descent iterations used in the ftting, as measured by training epochs or passes through the training set (Section 10.7). Notice that the training accuracy in Figure 10.11 (black points) increases monotonically in both cases. We can use the validation error to pick a good solution from each sequence (blue points in the plots), which would then be used to make predictions on the test data set.
Note that a two-class neural network amounts to a nonlinear logistic regression model. From (10.12) and (10.13) we can see that
\[\begin{aligned} \log\left(\frac{\Pr(Y=1|X)}{\Pr(Y=0|X)}\right) &= \quad Z\_1 - Z\_0 \\ &= \quad (\beta\_{10} - \beta\_{00}) + \sum\_{\ell=1}^{K\_2} (\beta\_{1\ell} - \beta\_{0\ell}) A\_{\ell}^{(2)} .\end{aligned}\]
(This shows the redundancy in the softmax function; for K classes we really only need to estimate K −1 sets of coefcients. See Section 4.3.5.) In Figure 10.11 we show accuracy (fraction correct) rather than classifcation accuracy error (fraction incorrect), the former being more popular in the machine learning community. Both models achieve a test-set accuracy of about 88%.
The bag-of-words model summarizes a document by the words present, and ignores their context. There are at least two popular ways to take the context into account:
• The bag-of-n-grams model. For example, a bag of 2-grams records bag-of-n-
grams
the consecutive co-occurrence of every distinct pair of words. “Blissfully long” can be seen as a positive phrase in a movie review, while “blissfully short” a negative.
• Treat the document as a sequence, taking account of all the words in the context of those that preceded and those that follow.
In the next section we explore models for sequences of data, which have applications in weather forecasting, speech recognition, language translation, and time-series prediction, to name a few. We continue with this IMDb example there.
10.5 Recurrent Neural Networks
Many data sources are sequential in nature, and call for special treatment when building predictive models. Examples include:
- Documents such as book and movie reviews, newspaper articles, and tweets. The sequence and relative positions of words in a document capture the narrative, theme and tone, and can be exploited in tasks such as topic classifcation, sentiment analysis, and language translation.
- Time series of temperature, rainfall, wind speed, air quality, and so on. We may want to forecast the weather several days ahead, or climate several decades ahead.
- Financial time series, where we track market indices, trading volumes, stock and bond prices, and exchange rates. Here prediction is often difcult, but as we will see, certain indices can be predicted with reasonable accuracy.
- Recorded speech, musical recordings, and other sound recordings. We may want to give a text transcription of a speech, or perhaps a language translation. We may want to assess the quality of a piece of music, or assign certain attributes.
- Handwriting, such as doctor’s notes, and handwritten digits such as zip codes. Here we want to turn the handwriting into digital text, or read the digits (optical character recognition).
In a recurrent neural network (RNN), the input object X is a sequence. recurrent neural network Consider a corpus of documents, such as the collection of IMDb movie reviews. Each document can be represented as a sequence of L words, so X = {X1, X2,…,XL}, where each Xℓ represents a word. The order of the words, and closeness of certain words in a sentence, convey semantic meaning. RNNs are designed to accommodate and take advantage of the sequential nature of such input objects, much like convolutional neural networks accommodate the spatial structure of image inputs. The output Y can also be a sequence (such as in language translation), but often is a scalar, like the binary sentiment label of a movie review document.
FIGURE 10.12. Schematic of a simple recurrent neural network. The input is a sequence of vectors {Xℓ}L 1 , and here the target is a single response. The network processes the input sequence X sequentially; each Xℓ feeds into the hidden layer, which also has as input the activation vector Aℓ−1 from the previous element in the sequence, and produces the current activation vector Aℓ. The same collections of weights W, U and B are used as each element of the sequence is processed. The output layer produces a sequence of predictions Oℓ from the current activation Aℓ, but typically only the last of these, OL, is of relevance. To the left of the equal sign is a concise representation of the network, which is unrolled into a more explicit version on the right.
Figure 10.12 illustrates the structure of a very basic RNN with a sequence X = {X1, X2,…,XL} as input, a simple output Y , and a hidden-layer sequence {Aℓ}L 1 = {A1, A2,…,AL}. Each Xℓ is a vector; in the document example Xℓ could represent a one-hot encoding for the ℓth word based on the language dictionary for the corpus (see the top panel in Figure 10.13 for a simple example). As the sequence is processed one vector Xℓ at a time, the network updates the activations Aℓ in the hidden layer, taking as input the vector Xℓ and the activation vector Aℓ−1 from the previous step in the sequence. Each Aℓ feeds into the output layer and produces a prediction Oℓ for Y . OL, the last of these, is the most relevant.
In detail, suppose each vector Xℓ of the input sequence has p components XT ℓ = (Xℓ1, Xℓ2,…,Xℓp), and the hidden layer consists of K units AT ℓ = (Aℓ1, Aℓ2,…,AℓK). As in Figure 10.4, we represent the collection of K × (p+ 1) shared weights wkj for the input layer by a matrix W, and similarly U is a K × K matrix of the weights uks for the hidden-to-hidden layers, and B is a K + 1 vector of weights βk for the output layer. Then
\[A\_{\ell k} = g\left(w\_{k0} + \sum\_{j=1}^{p} w\_{kj} X\_{\ell j} + \sum\_{s=1}^{K} u\_{ks} A\_{\ell - 1, s}\right),\tag{10.16}\]
and the output Oℓ is computed as
\[O\_{\ell} = \beta\_0 + \sum\_{k=1}^{K} \beta\_k A\_{\ell k} \tag{10.17}\]
for a quantitative response, or with an additional sigmoid activation function for a binary response, for example. Here g(·) is an activation function such as ReLU. Notice that the same weights W, U and B are used as we process each element in the sequence, i.e. they are not functions of ℓ. This is a form of weight sharing used by RNNs, and similar to the use of flters weight sharing in convolutional neural networks (Section 10.3.1.) As we proceed from beginning to end, the activations Aℓ accumulate a history of what has been seen before, so that the learned context can be used for prediction.
For regression problems the loss function for an observation (X, Y ) is
\[(Y - O\_L)^2,\tag{10.18}\]
which only references the fnal output OL = β0+#K k=1 βkALk. Thus O1, O2, …,OL−1 are not used. When we ft the model, each element Xℓ of the input sequence X contributes to OL via the chain (10.16), and hence contributes indirectly to learning the shared parameters W, U and B via the loss (10.18). With n input sequence/response pairs (xi, yi), the parameters are found by minimizing the sum of squares
\[\sum\_{i=1}^{n} (y\_i - o\_{iL})^2 = \sum\_{i=1}^{n} \left( y\_i - \left( \beta\_0 + \sum\_{k=1}^{K} \beta\_k g \left( w\_{k0} + \sum\_{j=1}^{p} w\_{kj} x\_{iLj} + \sum\_{s=1}^{K} u\_{ks} a\_{i,L-1,s} \right) \right) \right)^2. \tag{10.19}\]
Here we use lowercase letters for the observed yi and vector sequences xi = {xi1, xi2,…,xiL}, 15 as well as the derived activations.
Since the intermediate outputs Oℓ are not used, one may well ask why they are there at all. First of all, they come for free, since they use the same output weights B needed to produce OL, and provide an evolving prediction for the output. Furthermore, for some learning tasks the response is also a sequence, and so the output sequence {O1, O2,…,OL} is explicitly needed.
When used at full strength, recurrent neural networks can be quite complex. We illustrate their use in two simple applications. In the frst, we continue with the IMDb sentiment analysis of the previous section, where we process the words in the reviews sequentially. In the second application, we illustrate their use in a fnancial time series forecasting problem.
10.5.1 Sequential Models for Document Classifcation
Here we return to our classifcation task with the IMDb reviews. Our approach in Section 10.4 was to use the bag-of-words model. Here the plan is to use instead the sequence of words occurring in a document to make predictions about the label for the entire document.
We have, however, a dimensionality problem: each word in our document is represented by a one-hot-encoded vector (dummy variable) with 10,000 elements (one per word in the dictionary)! An approach that has become popular is to represent each word in a much lower-dimensional embedding embedding space. This means that rather than representing each word by a binary vector with 9,999 zeros and a single one in some position, we will represent it instead by a set of m real numbers, none of which are typically zero. Here m is the embedding dimension, and can be in the low 100s, or even less. This means (in our case) that we need a matrix E of dimension m×10,000,
15This is a sequence of vectors; each element xiℓ is a p-vector.
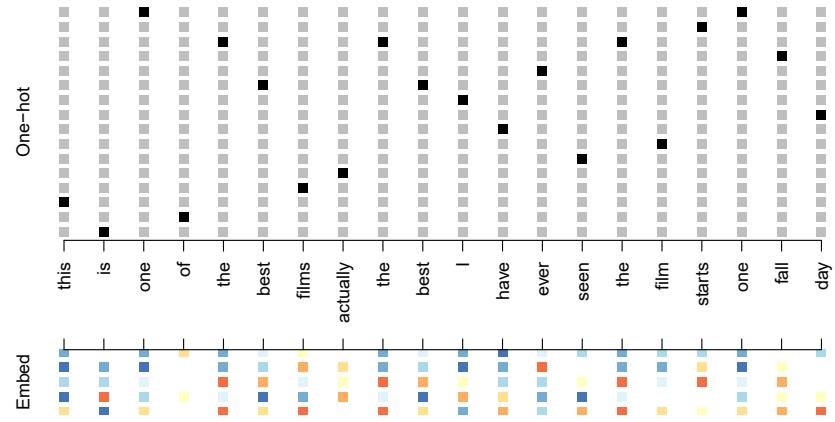
FIGURE 10.13. Depiction of a sequence of 20 words representing a single document: one-hot encoded using a dictionary of 16 words (top panel) and embedded in an m-dimensional space with m = 5 (bottom panel).
where each column is indexed by one of the 10,000 words in our dictionary, and the values in that column give the m coordinates for that word in the embedding space.
Figure 10.13 illustrates the idea (with a dictionary of 16 rather than 10,000, and m = 5). Where does E come from? If we have a large corpus of labeled documents, we can have the neural network learn E as part of the optimization. In this case E is referred to as an embedding layer, embedding layer and a specialized E is learned for the task at hand. Otherwise we can insert a precomputed matrix E in the embedding layer, a process known as weight freezing. Two pretrained embeddings, word2vec and GloVe, are weight widely used.16 These are built from a very large corpus of documents by a variant of principal components analysis (Section 12.2). The idea is that the positions of words in the embedding space preserve semantic meaning; e.g. synonyms should appear near each other.
So far, so good. Each document is now represented as a sequence of mvectors that represents the sequence of words. The next step is to limit each document to the last L words. Documents that are shorter than L get padded with zeros upfront. So now each document is represented by a series consisting of L vectors X = {X1, X2,…,XL}, and each Xℓ in the sequence has m components.
We now use the RNN structure in Figure 10.12. The training corpus consists of n separate series (documents) of length L, each of which gets processed sequentially from left to right. In the process, a parallel series of hidden activation vectors Aℓ, ℓ = 1,…,L is created as in (10.16) for each document. Aℓ feeds into the output layer to produce the evolving prediction Oℓ. We use the fnal value OL to predict the response: the sentiment of the review.
freezing word2vec GloVe
16 word2vec is described in Mikolov, Chen, Corrado, and Dean (2013), available at https://code.google.com/archive/p/word2vec. GloVe is described in Pennington, Socher, and Manning (2014), available at https://nlp.stanford.edu/projects/glove.
This is a simple RNN, and has relatively few parameters. If there are K hidden units, the common weight matrix W has K × (m + 1) parameters, the matrix U has K × K parameters, and B has 2(K + 1) for the two-class logistic regression as in (10.15). These are used repeatedly as we process the sequence X = {Xℓ}L 1 from left to right, much like we use a single convolution flter to process each patch in an image (Section 10.3.1). If the embedding layer E is learned, that adds an additional m × D parameters (D = 10,000 here), and is by far the biggest cost.
We ft the RNN as described in Figure 10.12 and the accompaying text to the IMDb data. The model had an embedding matrix E with m = 32 (which was learned in training as opposed to precomputed), followed by a single recurrent layer with K = 32 hidden units. The model was trained with dropout regularization on the 25,000 reviews in the designated training set, and achieved a disappointing 76% accuracy on the IMDb test data. A network using the GloVe pretrained embedding matrix E performed slightly worse.
For ease of exposition we have presented a very simple RNN. More elaborate versions use long term and short term memory (LSTM). Two tracks of hidden-layer activations are maintained, so that when the activation Aℓ is computed, it gets input from hidden units both further back in time, and closer in time — a so-called LSTM RNN. With long sequences, this LSTM RNN overcomes the problem of early signals being washed out by the time they get propagated through the chain to the fnal activation vector AL.
When we reft our model using the LSTM architecture for the hidden layer, the performance improved to 87% on the IMDb test data. This is comparable with the 88% achieved by the bag-of-words model in Section 10.4. We give details on ftting these models in Section 10.9.6.
Despite this added LSTM complexity, our RNN is still somewhat “entry level”. We could probably achieve slightly better results by changing the size of the model, changing the regularization, and including additional hidden layers. However, LSTM models take a long time to train, which makes exploring many architectures and parameter optimization tedious.
RNNs provide a rich framework for modeling data sequences, and they continue to evolve. There have been many advances in the development of RNNs — in architecture, data augmentation, and in the learning algorithms. At the time of this writing (early 2020) the leading RNN confgurations report accuracy above 95% on the IMDb data. The details are beyond the scope of this book.17
10.5.2 Time Series Forecasting
Figure 10.14 shows historical trading statistics from the New York Stock Exchange. Shown are three daily time series covering the period December 3, 1962 to December 31, 1986:18
17An IMDb leaderboard can be found at https://paperswithcode.com/sota/ sentiment-analysis-on-imdb.
18These data were assembled by LeBaron and Weigend (1998) IEEE Transactions on Neural Networks, 9(1): 213–220.
FIGURE 10.14. Historical trading statistics from the New York Stock Exchange. Daily values of the normalized log trading volume, DJIA return, and log volatility are shown for a 24-year period from 1962–1986. We wish to predict trading volume on any day, given the history on all earlier days. To the left of the red bar (January 2, 1980) is training data, and to the right test data.
- Log trading volume. This is the fraction of all outstanding shares that are traded on that day, relative to a 100-day moving average of past turnover, on the log scale.
- Dow Jones return. This is the diference between the log of the Dow Jones Industrial Index on consecutive trading days.
- Log volatility. This is based on the absolute values of daily price movements.
Predicting stock prices is a notoriously hard problem, but it turns out that predicting trading volume based on recent past history is more manageable (and is useful for planning trading strategies).
An observation here consists of the measurements (vt, rt, zt) on day t, in this case the values for log_volume, DJ_return and log_volatility. There are a total of T = 6,051 such triples, each of which is plotted as a time series in Figure 10.14. One feature that strikes us immediately is that the dayto-day observations are not independent of each other. The series exhibit auto-correlation — in this case values nearby in time tend to be similar autocorrelation to each other. This distinguishes time series from other data sets we have encountered, in which observations can be assumed to be independent of
Log( Trading Volume)
FIGURE 10.15. The autocorrelation function for log_volume. We see that nearby values are fairly strongly correlated, with correlations above 0.2 as far as 20 days apart.
each other. To be clear, consider pairs of observations (vt, vt−ℓ), a lag of ℓ lag days apart. If we take all such pairs in the vt series and compute their correlation coefcient, this gives the autocorrelation at lag ℓ. Figure 10.15 shows the autocorrelation function for all lags up to 37, and we see considerable correlation.
Another interesting characteristic of this forecasting problem is that the response variable vt — log_volume — is also a predictor! In particular, we will use the past values of log_volume to predict values in the future.
RNN forecaster
We wish to predict a value vt from past values vt−1, vt−2,…, and also to make use of past values of the other series rt−1, rt−2,… and zt−1, zt−2,…. Although our combined data is quite a long series with 6,051 trading days, the structure of the problem is diferent from the previous documentclassifcation example.
- We only have one series of data, not 25,000.
- We have an entire series of targets vt, and the inputs include past values of this series.
How do we represent this problem in terms of the structure displayed in Figure 10.12? The idea is to extract many short mini-series of input sequences X = {X1, X2,…,XL} with a predefned length L (called the lag lag in this context), and a corresponding target Y . They have the form
\[X\_1 = \begin{pmatrix} v\_{t-L} \\ r\_{t-L} \\ z\_{t-L} \end{pmatrix}, \ X\_2 = \begin{pmatrix} v\_{t-L+1} \\ r\_{t-L+1} \\ z\_{t-L+1} \end{pmatrix}, \ \cdots, X\_L = \begin{pmatrix} v\_{t-1} \\ r\_{t-1} \\ z\_{t-1} \end{pmatrix}, \ \text{and } Y = v\_t. \tag{10.20}\]
So here the target Y is the value of log_volume vt at a single timepoint t, and the input sequence X is the series of 3-vectors {Xℓ}L 1 each consisting of the three measurements log_volume, DJ_return and log_volatility from day t − L, t − L + 1, up to t − 1. Each value of t makes a separate (X, Y ) pair, for t running from L + 1 to T. For the NYSE data we will use the past
Test Period: Observed and Predicted
Year FIGURE 10.16. RNN forecast of log_volume on the NYSE test data. The black lines are the true volumes, and the superimposed orange the forecasts. The forecasted series accounts for 42% of the variance of log_volume.
fve trading days to predict the next day’s trading volume. Hence, we use L = 5. Since T = 6,051, we can create 6,046 such (X, Y ) pairs. Clearly L is a parameter that should be chosen with care, perhaps using validation data.
We ft this model with K = 12 hidden units using the 4,281 training sequences derived from the data before January 2, 1980 (see Figure 10.14), and then used it to forecast the 1,770 values of log_volume after this date. We achieve an R2 = 0.42 on the test data. Details are given in Section 10.9.6. As a straw man, 19 using yesterday’s value for log_volume as the prediction for today has R2 = 0.18. Figure 10.16 shows the forecast results. We have plotted the observed values of the daily log_volume for the test period 1980–1986 in black, and superimposed the predicted series in orange. The correspondence seems rather good.
In forecasting the value of log_volume in the test period, we have to use the test data itself in forming the input sequences X. This may feel like cheating, but in fact it is not; we are always using past data to predict the future.
Autoregression
The RNN we just ft has much in common with a traditional autoregression autoregression (AR) linear model, which we present now for comparison. We frst consider the response sequence vt alone, and construct a response vector y and a matrix M of predictors for least squares regression as follows:
\[\mathbf{y} = \begin{bmatrix} v\_{L+1} \\ v\_{L+2} \\ v\_{L+3} \\ \vdots \\ v\_T \end{bmatrix} \qquad \mathbf{M} = \begin{bmatrix} 1 & v\_L & v\_{L-1} & \cdots & v\_1 \\ 1 & v\_{L+1} & v\_L & \cdots & v\_2 \\ 1 & v\_{L+2} & v\_{L+1} & \cdots & v\_3 \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 1 & v\_{T-1} & v\_{T-2} & \cdots & v\_{T-L} \end{bmatrix} . \tag{10.21}\]
M and y each have T − L rows, one per observation. We see that the predictors for any given response vt on day t are the previous L values
19A straw man here refers to a simple and sensible prediction that can be used as a baseline for comparison.
of the same series. Fitting a regression of y on M amounts to ftting the model
\[ \hat{v}\_t = \hat{\beta}\_0 + \hat{\beta}\_1 v\_{t-1} + \hat{\beta}\_2 v\_{t-2} + \dots + \hat{\beta}\_L v\_{t-L},\tag{10.22} \]
and is called an order-L autoregressive model, or simply AR(L). For the NYSE data we can include lagged versions of DJ_return and log_volatility, rt and zt, in the predictor matrix M, resulting in 3L + 1 columns. An AR model with L = 5 achieves a test R2 of 0.41, slightly inferior to the 0.42 achieved by the RNN.
Of course the RNN and AR models are very similar. They both use the same response Y and input sequences X of length L = 5 and dimension p = 3 in this case. The RNN processes this sequence from left to right with the same weights W (for the input layer), while the AR model simply treats all L elements of the sequence equally as a vector of L × p predictors — a process called fattening in the neural network literature. fattening Of course the RNN also includes the hidden layer activations Aℓ which transfer information along the sequence, and introduces additional nonlinearity. From (10.19) with K = 12 hidden units, we see that the RNN has 13 + 12 × (1 + 3 + 12) = 205 parameters, compared to the 16 for the AR(5) model.
An obvious extension of the AR model is to use the set of lagged predictors as the input vector to an ordinary feedforward neural network (10.1), and hence add more fexibility. This achieved a test R2 = 0.42, slightly better than the linear AR, and the same as the RNN.
All the models can be improved by including the variable day_of_week corresponding to the day t of the target vt (which can be learned from the calendar dates supplied with the data); trading volume is often higher on Mondays and Fridays. Since there are fve trading days, this one-hot encodes to fve binary variables. The performance of the AR model improved to R2 = 0.46 as did the RNN, and the nonlinear AR model improved to R2 = 0.47.
We used the most simple version of the RNN in our examples here. Additional experiments with the LSTM extension of the RNN yielded small improvements, typically of up to 1% in R2 in these examples.
We give details of how we ft all three models in Section 10.9.6.
10.5.3 Summary of RNNs
We have illustrated RNNs through two simple use cases, and have only scratched the surface.
There are many variations and enhancements of the simple RNN we used for sequence modeling. One approach we did not discuss uses a onedimensional convolutional neural network, treating the sequence of vectors (say words, as represented in the embedding space) as an image. The convolution flter slides along the sequence in a one-dimensional fashion, with the potential to learn particular phrases or short subsequences relevant to the learning task.
One can also have additional hidden layers in an RNN. For example, with two hidden layers, the sequence Aℓ is treated as an input sequence to the next hidden layer in an obvious fashion.
The RNN we used scanned the document from beginning to end; alter-
native bidirectional RNNs scan the sequences in both directions. bidirectional In language translation the target is also a sequence of words, in a language diferent from that of the input sequence. Both the input sequence and the target sequence are represented by a structure similar to Figure 10.12, and they share the hidden units. In this so-called Seq2Seq Seq2Seq learning, the hidden units are thought to capture the semantic meaning of the sentences. Some of the big breakthroughs in language modeling and translation resulted from the relatively recent improvements in such RNNs.
Algorithms used to ft RNNs can be complex and computationally costly. Fortunately, good software protects users somewhat from these complexities, and makes specifying and ftting these models relatively painless. Many of the models that we enjoy in daily life (like Google Translate) use stateof-the-art architectures developed by teams of highly skilled engineers, and have been trained using massive computational and data resources.
10.6 When to Use Deep Learning
The performance of deep learning in this chapter has been rather impressive. It nailed the digit classifcation problem, and deep CNNs have really revolutionized image classifcation. We see daily reports of new success stories for deep learning. Many of these are related to image classifcation tasks, such as machine diagnosis of mammograms or digital X-ray images, ophthalmology eye scans, annotations of MRI scans, and so on. Likewise there are numerous successes of RNNs in speech and language translation, forecasting, and document modeling. The question that then begs an answer is: should we discard all our older tools, and use deep learning on every problem with data? To address this question, we revisit our Hitters dataset from Chapter 6.
This is a regression problem, where the goal is to predict the Salary of a baseball player in 1987 using his performance statistics from 1986. After removing players with missing responses, we are left with 263 players and 19 variables. We randomly split the data into a training set of 176 players (two thirds), and a test set of 87 players (one third). We used three methods for ftting a regression model to these data.
- A linear model was used to ft the training data, and make predictions on the test data. The model has 20 parameters.
- The same linear model was ft with lasso regularization. The tuning parameter was selected by 10-fold cross-validation on the training data. It selected a model with 12 variables having nonzero coefcients.
- A neural network with one hidden layer consisting of 64 ReLU units was ft to the data. This model has 1,345 parameters.20
20The model was ft by stochastic gradient descent with a batch size of 32 for 1,000 epochs, and 10% dropout regularization. The test error performance fattened out and started to slowly increase after 1,000 epochs. These ftting details are discussed in Section 10.7.
| Model | # Parameters | Mean Abs. Error | R2 Test Set |
|---|---|---|---|
| Linear Regression | 20 | 254.7 | 0.56 |
| Lasso | 12 | 252.3 | 0.51 |
| Neural Network | 1345 | 257.4 | 0.54 |
TABLE 10.2. Prediction results on the Hitters test data for linear models ft by ordinary least squares and lasso, compared to a neural network ft by stochastic gradient descent with dropout regularization.
| Coefcient | Std. error | t-statistic | p-value | |
|---|---|---|---|---|
| Intercept | -226.67 | 86.26 | -2.63 | 0.0103 |
| Hits | 3.06 | 1.02 | 3.00 | 0.0036 |
| Walks | 0.181 | 2.04 | 0.09 | 0.9294 |
| CRuns | 0.859 | 0.12 | 7.09 | < 0.0001 |
| PutOuts | 0.465 | 0.13 | 3.60 | 0.0005 |
TABLE 10.3. Least squares coefcient estimates associated with the regression of Salary on four variables chosen by lasso on the Hitters data set. This model achieved the best performance on the test data, with a mean absolute error of 224.8. The results reported here were obtained from a regression on the test data, which was not used in ftting the lasso model.
Table 10.2 compares the results. We see similar performance for all three models. We report the mean absolute error on the test data, as well as the test R2 for each method, which are all respectable (see Exercise 5). We spent a fair bit of time fddling with the confguration parameters of the neural network to achieve these results. It is possible that if we were to spend more time, and got the form and amount of regularization just right, that we might be able to match or even outperform linear regression and the lasso. But with great ease we obtained linear models that work well. Linear models are much easier to present and understand than the neural network, which is essentially a black box. The lasso selected 12 of the 19 variables in making its prediction. So in cases like this we are much better of following the Occam’s razor principle: when faced with several methods Occam’s razor that give roughly equivalent performance, pick the simplest.
After a bit more exploration with the lasso model, we identifed an even simpler model with four variables. We then reft the linear model with these four variables to the training data (the so-called relaxed lasso), and achieved a test mean absolute error of 224.8, the overall winner! It is tempting to present the summary table from this ft, so we can see coefcients and pvalues; however, since the model was selected on the training data, there would be selection bias. Instead, we reft the model on the test data, which was not used in the selection. Table 10.3 shows the results.
We have a number of very powerful tools at our disposal, including neural networks, random forests and boosting, support vector machines and generalized additive models, to name a few. And then we have linear models, and simple variants of these. When faced with new data modeling and prediction problems, it’s tempting to always go for the trendy new methods. Often they give extremely impressive results, especially when the datasets are very large and can support the ftting of high-dimensional nonlinear models. However, if we can produce models with the simpler tools that
perform as well, they are likely to be easier to ft and understand, and potentially less fragile than the more complex approaches. Wherever possible, it makes sense to try the simpler models as well, and then make a choice based on the performance/complexity tradeof.
Typically we expect deep learning to be an attractive choice when the sample size of the training set is extremely large, and when interpretability of the model is not a high priority.
10.7 Fitting a Neural Network
Fitting neural networks is somewhat complex, and we give a brief overview here. The ideas generalize to much more complex networks. Readers who fnd this material challenging can safely skip it. Fortunately, as we see in the lab at the end of this chapter, good software is available to ft neural network models in a relatively automated way, without worrying about the technical details of the model-ftting procedure.
We start with the simple network depicted in Figure 10.1 in Section 10.1. In model (10.1) the parameters are β = (β0, β1,…, βK), as well as each of the wk = (wk0, wk1,…,wkp), k = 1, . . . , K. Given observations (xi, yi), i = 1, . . . , n, we could ft the model by solving a nonlinear least squares problem
\[\underset{\{w\_k\}\_1^K, \beta}{\text{minimize}} \frac{1}{2} \sum\_{i=1}^n (y\_i - f(x\_i))^2,\tag{10.23}\]
where
\[f(x\_i) = \beta\_0 + \sum\_{k=1}^{K} \beta\_k g\left(w\_{k0} + \sum\_{j=1}^{p} w\_{kj} x\_{ij}\right). \tag{10.24}\]
The objective in (10.23) looks simple enough, but because of the nested arrangement of the parameters and the symmetry of the hidden units, it is not straightforward to minimize. The problem is nonconvex in the parameters, and hence there are multiple solutions. As an example, Figure 10.17 shows a simple nonconvex function of a single variable θ; there are two solutions: one is a local minimum and the other is a global minimum. Fur- local thermore, (10.1) is the very simplest of neural networks; in this chapter we have presented much more complex ones where these problems are compounded. To overcome some of these issues and to protect from overftting, two general strategies are employed when ftting neural networks.
- minimum global minimum
- Slow Learning: the model is ft in a somewhat slow iterative fashion, using gradient descent. The ftting process is then stopped when gradient descent overftting is detected.
- Regularization: penalties are imposed on the parameters, usually lasso or ridge as discussed in Section 6.2.
Suppose we represent all the parameters in one long vector θ. Then we can rewrite the objective in (10.23) as
\[R(\theta) = \frac{1}{2} \sum\_{i=1}^{n} (y\_i - f\_{\theta}(x\_i))^2,\tag{10.25}\]
FIGURE 10.17. Illustration of gradient descent for one-dimensional θ. The objective function R(θ) is not convex, and has two minima, one at θ = −0.46 (local), the other at θ = 1.02 (global). Starting at some value θ0 (typically randomly chosen), each step in θ moves downhill — against the gradient — until it cannot go down any further. Here gradient descent reached the global minimum in 7 steps.
where we make explicit the dependence of f on the parameters. The idea of gradient descent is very simple.
- Start with a guess θ0 for all the parameters in θ, and set t = 0.
- Iterate until the objective (10.25) fails to decrease:
- Find a vector δ that refects a small change in θ, such that θt+1 = θt + δ reduces the objective; i.e. such that R(θt+1) < R(θt ).
- Set t ← t + 1.
One can visualize (Figure 10.17) standing in a mountainous terrain, and the goal is to get to the bottom through a series of steps. As long as each step goes downhill, we must eventually get to the bottom. In this case we were lucky, because with our starting guess θ0 we end up at the global minimum. In general we can hope to end up at a (good) local minimum.
10.7.1 Backpropagation
How do we fnd the directions to move θ so as to decrease the objective R(θ) in (10.25)? The gradient of R(θ), evaluated at some current value θ = θm, gradient is the vector of partial derivatives at that point:
\[\nabla R(\theta^m) = \frac{\partial R(\theta)}{\partial \theta}\Big|\_{\theta = \theta^m} \,. \tag{10.26}\]
The subscript θ = θm means that after computing the vector of derivatives, we evaluate it at the current guess, θm. This gives the direction in θ-space in which R(θ) increases most rapidly. The idea of gradient descent is to move θ a little in the opposite direction (since we wish to go downhill):
\[ \theta^{m+1} \leftarrow \theta^m - \rho \nabla R(\theta^m). \tag{10.27} \]
For a small enough value of the learning rate ρ, this step will decrease the learning rate objective R(θ); i.e. R(θm+1) ≤ R(θm). If the gradient vector is zero, then we may have arrived at a minimum of the objective.
How complicated is the calculation (10.26)? It turns out that it is quite simple here, and remains simple even for much more complex networks,
because of the chain rule of diferentiation. chain rule Since R(θ) = #n i=1 Ri(θ) = 1 2 #n i=1(yi − fθ(xi))2 is a sum, its gradient is also a sum over the n observations, so we will just examine one of these terms,
\[R\_i(\theta) = \frac{1}{2} \left( y\_i - \beta\_0 - \sum\_{k=1}^{K} \beta\_k g \left( w\_{k0} + \sum\_{j=1}^{p} w\_{kj} x\_{ij} \right) \right)^2. \tag{10.28}\]
To simplify the expressions to follow, we write zik = wk0 + #p j=1 wkjxij . First we take the derivative with respect to βk:
\[\begin{split} \frac{\partial R\_i(\theta)}{\partial \beta\_k} &= \quad \frac{\partial R\_i(\theta)}{\partial f\_\theta(x\_i)} \cdot \frac{\partial f\_\theta(x\_i)}{\partial \beta\_k} \\ &= \quad -(y\_i - f\_\theta(x\_i)) \cdot g(z\_{ik}). \end{split} \tag{10.29}\]
And now we take the derivative with respect to wkj :
\[\frac{\partial R\_i(\theta)}{\partial w\_{kj}} = \frac{\partial R\_i(\theta)}{\partial f\_\theta(x\_i)} \cdot \frac{\partial f\_\theta(x\_i)}{\partial g(z\_{ik})} \cdot \frac{\partial g(z\_{ik})}{\partial z\_{ik}} \cdot \frac{\partial z\_{ik}}{\partial w\_{kj}}\]
\[= \quad - (y\_i - f\_\theta(x\_i)) \cdot \beta\_k \cdot g'(z\_{ik}) \cdot x\_{ij}.\tag{10.30}\]
Notice that both these expressions contain the residual yi − fθ(xi). In (10.29) we see that a fraction of that residual gets attributed to each of the hidden units according to the value of g(zik). Then in (10.30) we see a similar attribution to input j via hidden unit k. So the act of diferentiation assigns a fraction of the residual to each of the parameters via the chain rule — a process known as backpropagation in the neural network backpropagation literature. Although these calculations are straightforward, it takes careful bookkeeping to keep track of all the pieces.
10.7.2 Regularization and Stochastic Gradient Descent
Gradient descent usually takes many steps to reach a local minimum. In practice, there are a number of approaches for accelerating the process. Also, when n is large, instead of summing (10.29)–(10.30) over all n observations, we can sample a small fraction or minibatch of them each time minibatch we compute a gradient step. This process is known as stochastic gradient descent (SGD) and is the state of the art for learning deep neural networks. stochastic Fortunately, there is very good software for setting up deep learning models, and for ftting them to data, so most of the technicalities are hidden from the user.
We now turn to the multilayer network (Figure 10.4) used in the digit recognition problem. The network has over 235,000 weights, which is around four times the number of training examples. Regularization is essential here
gradient descent
FIGURE 10.18. Evolution of training and validation errors for the MNIST neural network depicted in Figure 10.4, as a function of training epochs. The objective refers to the log-likelihood (10.14).
to avoid overftting. The frst row in Table 10.1 uses ridge regularization on the weights. This is achieved by augmenting the objective function (10.14) with a penalty term:
\[R(\theta;\lambda) = -\sum\_{i=1}^{n} \sum\_{m=0}^{9} y\_{im} \log(f\_m(x\_i)) + \lambda \sum\_{j} \theta\_j^2. \tag{10.31}\]
The parameter λ is often preset at a small value, or else it is found using the validation-set approach of Section 5.3.1. We can also use diferent values of λ for the groups of weights from diferent layers; in this case W1 and W2 were penalized, while the relatively few weights B of the output layer were not penalized at all. Lasso regularization is also popular as an additional form of regularization, or as an alternative to ridge.
Figure 10.18 shows some metrics that evolve during the training of the network on the MNIST data. It turns out that SGD naturally enforces its own form of approximately quadratic regularization.21 Here the minibatch size was 128 observations per gradient update. The term epochs labeling the epochs horizontal axis in Figure 10.18 counts the number of times an equivalent of the full training set has been processed. For this network, 20% of the 60,000 training observations were used as a validation set in order to determine when training should stop. So in fact 48,000 observations were used for training, and hence there are 48,000/128 ≈ 375 minibatch gradient updates per epoch. We see that the value of the validation objective actually starts to increase by 30 epochs, so early stopping can also be used as an additional early stopping form of regularization.
21This and other properties of SGD for deep learning are the subject of much research in the machine learning literature at the time of writing.
FIGURE 10.19. Dropout Learning. Left: a fully connected network. Right: network with dropout in the input and hidden layer. The nodes in grey are selected at random, and ignored in an instance of training.
10.7.3 Dropout Learning
The second row in Table 10.1 is labeled dropout. This is a relatively new dropout and efcient form of regularization, similar in some respects to ridge regularization. Inspired by random forests (Section 8.2), the idea is to randomly remove a fraction φ of the units in a layer when ftting the model. Figure 10.19 illustrates this. This is done separately each time a training observation is processed. The surviving units stand in for those missing, and their weights are scaled up by a factor of 1/(1 − φ) to compensate. This prevents nodes from becoming over-specialized, and can be seen as a form of regularization. In practice dropout is achieved by randomly setting the activations for the “dropped out” units to zero, while keeping the architecture intact.
10.7.4 Network Tuning
The network in Figure 10.4 is considered to be relatively straightforward; it nevertheless requires a number of choices that all have an efect on the performance:
- The number of hidden layers, and the number of units per layer. Modern thinking is that the number of units per hidden layer can be large, and overftting can be controlled via the various forms of regularization.
- Regularization tuning parameters. These include the dropout rate φ and the strength λ of lasso and ridge regularization, and are typically set separately at each layer.
- Details of stochastic gradient descent. These include the batch size, the number of epochs, and if used, details of data augmentation (Section 10.3.4.)
Choices such as these can make a diference. In preparing this MNIST example, we achieved a respectable 1.8% misclassifcation error after some trial and error. Finer tuning and training of a similar network can get under 1% error on these data, but the tinkering process can be tedious, and can result in overftting if done carelessly.
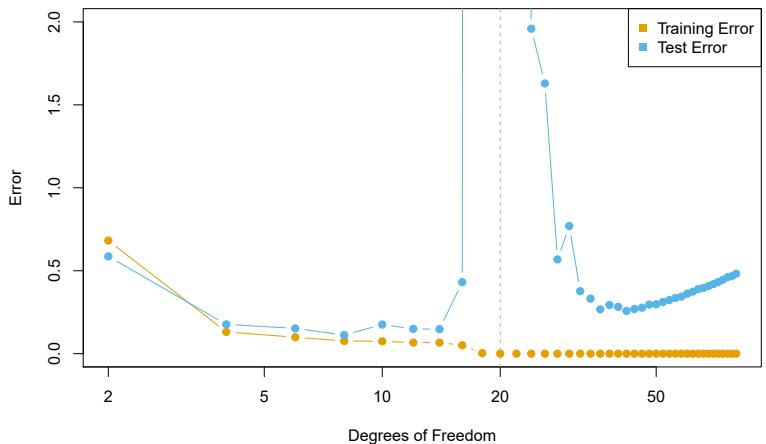
FIGURE 10.20. Double descent phenomenon, illustrated using error plots for a one-dimensional natural spline example. The horizontal axis refers to the number of spline basis functions on the log scale. The training error hits zero when the degrees of freedom coincides with the sample size n = 20, the “interpolation threshold”, and remains zero thereafter. The test error increases dramatically at this threshold, but then descends again to a reasonable value before fnally increasing again.
10.8 Interpolation and Double Descent
Throughout this book, we have repeatedly discussed the bias-variance tradeof, frst presented in Section 2.2.2. This trade-of indicates that statistical learning methods tend to perform the best, in terms of test-set error, for an intermediate level of model complexity. In particular, if we plot “fexibility” on the x-axis and error on the y-axis, then we generally expect to see that test error has a U-shape, whereas training error decreases monotonically. Two “typical” examples of this behavior can be seen in the right-hand panel of Figure 2.9 on page 29, and in Figure 2.17 on page 39. One implication of the bias-variance trade-of is that it is generally not a good idea to interpolate the training data — that is, to get zero training error — since interpolate that will often result in very high test error.
However, it turns out that in certain specifc settings it can be possible for a statistical learning method that interpolates the training data to perform well — or at least, better than a slightly less complex model that does not quite interpolate the data. This phenomenon is known as double descent, and is displayed in Figure 10.20. “Double descent” gets its name from the fact that the test error has a U-shape before the interpolation threshold is reached, and then it descends again (for a while, at least) as an increasingly fexible model is ft.
We now describe the set-up that resulted in Figure 10.20. We simulated n = 20 observations from the model
\[Y = \sin(X) + \epsilon,\]
where X ∼ U[−5, 5] (uniform distribution), and ϵ ∼ N(0, σ2) with σ = 0.3. We then ft a natural spline to the data, as described in Section 7.4, with d
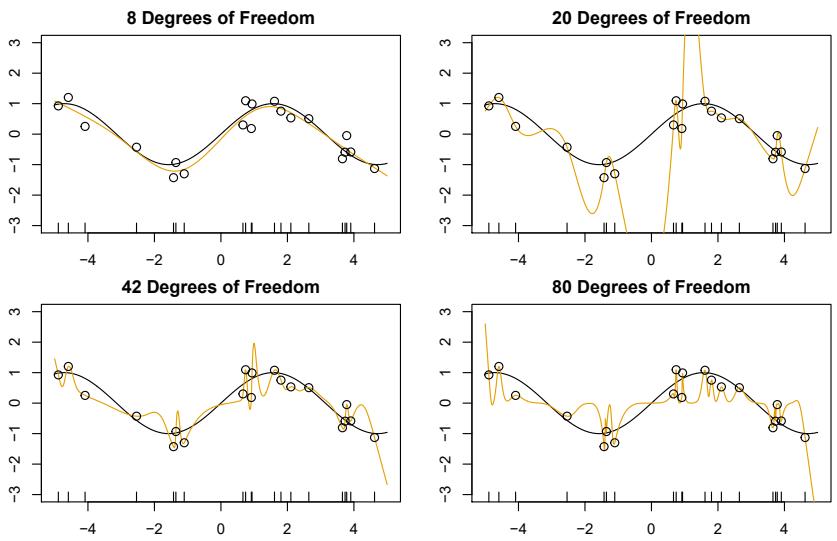
FIGURE 10.21. Fitted functions ˆfd(X) (orange), true function f(X) (black) and the observed 20 training data points. A diferent value of d (degrees of freedom) is used in each panel. For d ≥ 20 the orange curves all interpolate the training points, and hence the training error is zero.
degrees of freedom.22 Recall from Section 7.4 that ftting a natural spline with d degrees of freedom amounts to ftting a least-squares regression of the response onto a set of d basis functions. The upper-left panel of Figure 10.21 shows the data, the true function f(X), and ˆf8(X), the ftted natural spline with d = 8 degrees of freedom.
Next, we ft a natural spline with d = 20 degrees of freedom. Since n = 20, this means that n = d, and we have zero training error; in other words, we have interpolated the training data! We can see from the top-right panel of Figure 10.21 that ˆf20(X) makes wild excursions, and hence the test error will be large.
We now continue to ft natural splines to the data, with increasing values of d. For d > 20, the least squares regression of Y onto d basis functions is not unique: there are an infnite number of least squares coefcient estimates that achieve zero error. To select among them, we choose the one with the smallest sum of squared coefcients, #d j=1 βˆ2 j . This is known as the minimum-norm solution.
The two lower panels of Figure 10.21 show the minimum-norm natural spline fts with d = 42 and d = 80 degrees of freedom. Incredibly, ˆf42(X) is quite a bit less less wild than ˆf20(X), even though it makes use of more degrees of freedom. And ˆf80(X) is not much diferent. How can this be? Essentially, ˆf20(X) is very wild because there is just a single way to interpolate n = 20 observations using d = 20 basis functions, and that single way results in a somewhat extreme ftted function. By contrast, there are an
22This implies the choice of d knots, here chosen at d equi-probability quantiles of the training data. When d>n, the quantiles are found by interpolation.
infnite number of ways to interpolate n = 20 observations using d = 42 or d = 80 basis functions, and the smoothest of them — that is, the minimum norm solution — is much less wild than ˆf20(X)!
In Figure 10.20, we display the training error and test error associated with ˆfd(X), for a range of values of the degrees of freedom d. We see that the training error drops to zero once d = 20 and beyond; i.e. once the interpolation threshold is reached. By contrast, the test error shows a Ushape for d ≤ 20, grows extremely large around d = 20, and then shows a second region of descent for d > 20. For this example the signal-to-noise ratio — Var(f(X))/σ2 — is 5.9, which is quite high (the data points are close to the true curve). So an estimate that interpolates the data and does not wander too far inbetween the observed data points will likely do well.
In Figures 10.20 and 10.21, we have illustrated the double descent phenomenon in a simple one-dimensional setting using natural splines. However, it turns out that the same phenomenon can arise for deep learning. Basically, when we ft neural networks with a huge number of parameters, we are sometimes able to get good results with zero training error. This is particularly true in problems with high signal-to-noise ratio, such as natural image recognition and language translation, for example. This is because the techniques used to ft neural networks, including stochastic gradient descent, naturally lend themselves to selecting a “smooth” interpolating model that has good test-set performance on these kinds of problems.
Some points are worth emphasizing:
- The double-descent phenomenon does not contradict the bias-variance trade-of, as presented in Section 2.2.2. Rather, the double-descent curve seen in the right-hand side of Figure 10.20 is a consequence of the fact that the x-axis displays the number of spline basis functions used, which does not properly capture the true “fexibility” of models that interpolate the training data. Stated another way, in this example, the minimum-norm natural spline with d = 42 has lower variance than the natural spline with d = 20.
- Most of the statistical learning methods seen in this book do not exhibit double descent. For instance, regularization approaches typically do not interpolate the training data, and thus double descent does not occur. This is not a drawback of regularized methods: they can give great results without interpolating the data!
In particular, in the examples here, if we had ft the natural splines using ridge regression with an appropriately-chosen penalty rather than least squares, then we would not have seen double descent, and in fact would have obtained better test error results.
- In Chapter 9, we saw that maximal margin classifers and SVMs that have zero training error nonetheless often achieve very good test error. This is in part because those methods seek smooth minimum norm solutions. This is similar to the fact that the minimum-norm natural spline can give good results with zero training error.
- The double-descent phenomenon has been used by the machine learning community to explain the successful practice of using an over-
parametrized neural network (many layers, and many hidden units), and then ftting all the way to zero training error. However, ftting to zero error is not always optimal, and whether it is advisable depends on the signal-to-noise ratio. For instance, we may use ridge regularization to avoid overftting a neural network, as in (10.31). In this case, provided that we use an appropriate choice for the tuning parameter λ, we will never interpolate the training data, and thus will not see the double descent phenomenon. Nonetheless we can get very good test-set performance, likely much better than we would have achieved had we interpolated the training data. Early stopping during stochastic gradient descent can also serve as a form of regularization that prevents us from interpolating the training data, while still getting very good results on test data.
To summarize: though double descent can sometimes occur in neural networks, we typically do not want to rely on this behavior. Moreover, it is important to remember that the bias-variance trade-of always holds (though it is possible that test error as a function of fexibility may not exhibit a U-shape, depending on how we have parametrized the notion of “fexibility” on the x-axis).
10.9 Lab: Deep Learning
In this section we demonstrate how to ft the examples discussed in the text. We use the Python torch package, along with the pytorch_lightning torch package which provides utilities to simplify ftting and evaluating models. This code can be impressively fast with certain special processors, such as Apple’s new M1 chip. The package is well-structured, fexible, and will feel comfortable to Python users. A good companion is the site pytorch.org/tutorials. Much of our code is adapted from there, as well as the pytorch_lightning documentation.23
pytorch_ lightning
We start with several standard imports that we have seen before.
In [1]: import numpy as np, pandas as pd
from matplotlib.pyplot import subplots
from sklearn.linear_model import \
(LinearRegression,
LogisticRegression,
Lasso)
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import KFold
from sklearn.pipeline import Pipeline
from ISLP import load_data
from ISLP.models import ModelSpec as MS
from sklearn.model_selection import \
(train_test_split,
GridSearchCV)23The precise URLs at the time of writing are https://pytorch.org/tutorials/ beginner/basics/intro.html and https://pytorch-lightning.readthedocs.io/en/ latest/.
436 10. Deep Learning
Torch-Specifc Imports
There are a number of imports for torch. (These are not included with ISLP, so must be installed separately.) First we import the main library and essential tools used to specify sequentially-structured networks.
In [2]: import torch
from torch import nn
from torch.optim import RMSprop
from torch.utils.data import TensorDatasetThere are several other helper packages for torch. For instance, the torchmetrics package has utilities to compute various metrics to evalu- torchmetrics ate performance when ftting a model. The torchinfo package provides a torchinfo useful summary of the layers of a model. We use the read_image() function read_image() when loading test images in Section 10.9.4.
In [3]: from torchmetrics import (MeanAbsoluteError,
R2Score)
from torchinfo import summary
from torchvision.io import read_imageThe package pytorch_lightning is a somewhat higher-level interface to torch that simplifes the specifcation and ftting of models by reducing the amount of boilerplate code needed (compared to using torch alone).
In [4]: from pytorch_lightning import Trainer
from pytorch_lightning.loggers import CSVLoggerIn order to reproduce results we use seed_everything(). We will also seed_ everything() instruct torch to use deterministic algorithms where possible.
In [5]: from pytorch_lightning.utilities.seed import seed_everything
seed_everything(0, workers=True)
torch.use_deterministic_algorithms(True, warn_only=True)We will use several datasets shipped with torchvision for our examples: torchvision a pretrained network for image classifcation, as well as some transforms used for preprocessing.
In [6]: from torchvision.datasets import MNIST, CIFAR100
from torchvision.models import (resnet50,
ResNet50_Weights)
from torchvision.transforms import (Resize,
Normalize,
CenterCrop,
ToTensor)We have provided a few utilities in ISLP specifcally for this lab. The SimpleDataModule and SimpleModule are simple versions of objects used in pytorch_lightning, the high-level module for ftting torch models. Although more advanced uses such as computing on graphical processing units (GPUs) and parallel data processing are possible in this module, we will not be focusing much on these in this lab. The ErrorTracker handles collections of targets and predictions over each mini-batch in the validation or test stage, allowing computation of the metric over the entire validation or test data set.
In [7]: from ISLP.torch import (SimpleDataModule,
SimpleModule,
ErrorTracker,
rec_num_workers)In addition we have included some helper functions to load the IMDb database, as well as a lookup that maps integers to particular keys in the database. We’ve included a slightly modifed copy of the preprocessed IMDb data from keras, a separate package for ftting deep learning models. This keras saves us signifcant preprocessing and allows us to focus on specifying and ftting the models themselves.
In [8]: from ISLP.torch.imdb import (load_lookup,
load_tensor,
load_sparse,
load_sequential)Finally, we introduce some utility imports not directly related to torch. The glob() function from the glob module is used to fnd all fles matching glob() wildcard characters, which we will use in our example applying the ResNet50 model to some of our own images. The json module will be used to load a json JSON fle for looking up classes to identify the labels of the pictures in the ResNet50 example.
In [9]: from glob import glob import json
10.9.1 Single Layer Network on Hitters Data
We start by ftting the models in Section 10.6 on the Hitters data.
In [10]: Hitters = load_data('Hitters').dropna()
n = Hitters.shape[0]We will ft two linear models (least squares and lasso) and compare their performance to that of a neural network. For this comparison we will use mean absolute error on a validation dataset.
\[\text{MAE}(y, \hat{y}) = \frac{1}{n} \sum\_{i=1}^{n} |y\_i - \hat{y}\_i|.\]
We set up the model matrix and the response.
In [11]: model = MS(Hitters.columns.drop('Salary'), intercept=False)
X = model.fit_transform(Hitters).to_numpy()
Y = Hitters['Salary'].to_numpy()The to_numpy() method above converts pandas data frames or series to to_numpy() numpy arrays. We do this because we will need to use sklearn to ft the lasso model, and it requires this conversion. We also use a linear regression method from sklearn, rather than the method in Chapter 3 from statsmodels, to facilitate the comparisons.
We now split the data into test and training, fxing the random state used by sklearn to do the split.
In [12]: (X_train,
X_test,
Y_train,
Y_test) = train_test_split(X,
Y,
test_size=1/3,
random_state=1)Linear Models
We ft the linear model and evaluate the test error directly.
In [13]: hit_lm = LinearRegression().fit(X_train, Y_train)
Yhat_test = hit_lm.predict(X_test)
np.abs(Yhat_test - Y_test).mean()Out[13]: 259.7153
Next we ft the lasso using sklearn. We are using mean absolute error to select and evaluate a model, rather than mean squared error. The specialized solver we used in Section 6.5.2 uses only mean squared error. So here, with a bit more work, we create a cross-validation grid and perform the cross-validation directly.
We encode a pipeline with two steps: we frst normalize the features using a StandardScaler() transform, and then ft the lasso without further normalization.
In [14]: scaler = StandardScaler(with_mean=True, with_std=True)
lasso = Lasso(warm_start=True, max_iter=30000)
standard_lasso = Pipeline(steps=[('scaler', scaler),
('lasso', lasso)])We need to create a grid of values for λ. As is common practice, we choose a grid of 100 values of λ, uniform on the log scale from lam_max down to 0.01*lam_max. Here lam_max is the smallest value of λ with an allzero solution. This value equals the largest absolute inner-product between any predictor and the (centered) response.24
In [15]: X_s = scaler.fit_transform(X_train)
n = X_s.shape[0]
lam_max = np.fabs(X_s.T.dot(Y_train - Y_train.mean())).max() / n
param_grid = {'alpha': np.exp(np.linspace(0, np.log(0.01), 100))
* lam_max}Note that we had to transform the data frst, since the scale of the variables impacts the choice of λ. We now perform cross-validation using this sequence of λ values.
In [16]: cv = KFold(10, shuffle=True, random_state=1) grid = GridSearchCV(lasso,
24The derivation of this result is beyond the scope of this book.
param_grid,
cv=cv,
scoring='neg_mean_absolute_error')
grid.fit(X_train, Y_train);We extract the lasso model with best cross-validated mean absolute error, and evaluate its performance on X_test and Y_test, which were not used in cross-validation.
In [17]: trained_lasso = grid.best_estimator_
Yhat_test = trained_lasso.predict(X_test)
np.fabs(Yhat_test - Y_test).mean()Out[17]: 257.2382
This is similar to the results we got for the linear model ft by least squares. However, these results can vary a lot for diferent train/test splits; we encourage the reader to try a diferent seed in code block 12 and rerun the subsequent code up to this point.
Specifying a Network: Classes and Inheritance
To ft the neural network, we frst set up a model structure that describes the network. Doing so requires us to defne new classes specifc to the model we wish to ft. Typically this is done in pytorch by sub-classing a generic representation of a network, which is the approach we take here. Although this example is simple, we will go through the steps in some detail, since it will serve us well for the more complex examples to follow.
In [18]: class HittersModel(nn.Module):
def __init__(self, input_size):
super(HittersModel , self).__init__()
self.flatten = nn.Flatten()
self.sequential = nn.Sequential(
nn.Linear(input_size, 50),
nn.ReLU(),
nn.Dropout(0.4),
nn.Linear(50, 1))
def forward(self, x):
x = self.flatten(x)
return torch.flatten(self.sequential(x))The class statement identifes the code chunk as a declaration for a class HittersModel that inherits from the base class nn.Module. This base class is ubiquitous in torch and represents the mappings in the neural networks.
Indented beneath the class statement are the methods of this class: in this case __init__ and forward. The __init__ method is called when an instance of the class is created as in the cell below. In the methods, self always refers to an instance of the class. In the __init__ method, we have attached two objects to self as attributes: flatten and sequential. These are used in the forward method to describe the map that this module implements.
440 10. Deep Learning
There is one additional line in the __init__ method, which is a call to super(). This function allows subclasses (i.e. HittersModel) to access meth- super() ods of the class they inherit from. For example, the class nn.Module has its own __init__ method, which is diferent from the HittersModel.__init__() method we’ve written above. Using super() allows us to call the method of the base class. For torch models, we will always be making this super() call as it is necessary for the model to be properly interpreted by torch.
The object nn.Module has more methods than simply __init__ and forward. These methods are directly accessible to HittersModel instances because of this inheritance. One such method we will see shortly is the eval() method, used to disable dropout for when we want to evaluate the model on test data.
In [19]: hit_model = HittersModel(X.shape[1])The object self.sequential is a composition of four maps. The frst maps the 19 features of Hitters to 50 dimensions, introducing 50 × 19 + 50 parameters for the weights and intercept of the map (often called the bias). This layer is then mapped to a ReLU layer followed by a 40% dropout layer, and fnally a linear map down to 1 dimension, again with a bias. The total number of trainable parameters is therefore 50 × 19 + 50 + 50 + 1 = 1051.
The package torchinfo provides a summary() function that neatly summarizes this information. We specify the size of the input and see the size of each tensor as it passes through layers of the network.
In [20]: summary(hit_model,
input_size=X_train.shape,
col_names=['input_size',
'output_size',
'num_params'])| Layer | Input | Output | Param |
|---|---|---|---|
| (type:depth-idx) | Shape | Shape | # |
| ===================================================================== HittersModel |
[175, 19] |
[175] | – |
| Flatten: | [175, | [175, | – |
| 1-1 | 19] | 19] | |
| Sequential: | [175, | [175, | – |
| 1-2 | 19] | 1] | |
| Linear: | [175, | [175, | 1,000 |
| 2-1 | 19] | 50] | |
| ReLU: | [175, | [175, | – |
| 2-2 | 50] | 50] | |
| Dropout: | [175, | [175, | – |
| 2-3 | 50] | 50] | |
| Linear: | [175, | [175, | 51 |
| 2-4 | 50] | 1] |
Total params: 1,051 Trainable params: 1,051
We have truncated the end of the output slightly, here and in subsequent uses.
We now need to transform our training data into a form accessible to torch. The basic datatype in torch is a tensor, which is very similar to an ndarray from early chapters. We also note here that torch typically works with 32-bit (single precision) rather than 64-bit (double precision) foating point numbers. We therefore convert our data to np.float32 before forming the tensor. The X and Y tensors are then arranged into a Dataset Dataset
recognized by torch using TensorDataset(). Tensor
Dataset() In [21]: X_train_t = torch.tensor(X_train.astype(np.float32))
Y_train_t = torch.tensor(Y_train.astype(np.float32))
hit_train = TensorDataset(X_train_t, Y_train_t)We do the same for the test data.
In [22]: X_test_t = torch.tensor(X_test.astype(np.float32))
Y_test_t = torch.tensor(Y_test.astype(np.float32))
hit_test = TensorDataset(X_test_t, Y_test_t)Finally, this dataset is passed to a DataLoader() which ultimately passes data into our network. While this may seem like a lot of overhead, this structure is helpful for more complex tasks where data may live on diferent machines, or where data must be passed to a GPU. We provide a helper function SimpleDataModule() in ISLP to make this task easier for standard SimpleData Module() usage. One of its arguments is num_workers, which indicates how many processes we will use for loading the data. For small data like Hitters this will have little efect, but it does provide an advantage for the MNIST and CIFAR100 examples below. The torch package will inspect the process running and determine a maximum number of workers.25 We’ve included a function rec_num_workers() to compute this so we know how many workers might be reasonable (here the max was 16).
In [23]: max_num_workers = rec_num_workers()The general training setup in pytorch_lightning involves training, validation and test data. These are each represented by diferent data loaders. During each epoch, we run a training step to learn the model and a validation step to track the error. The test data is typically used at the end of training to evaluate the model.
In this case, as we had split only into test and training, we’ll use the test data as validation data with the argument validation=hit_test. The validation argument can be a foat between 0 and 1, an integer, or a Dataset. If a foat (respectively, integer), it is interpreted as a percentage (respectively number) of the training observations to be used for validation. If it is a Dataset, it is passed directly to a data loader.
In [24]: hit_dm = SimpleDataModule(hit_train,
hit_test,
batch_size=32,
num_workers=min(4, max_num_workers),
validation=hit_test)Next we must provide a pytorch_lightning module that controls the steps performed during the training process. We provide methods for our SimpleModule() that simply record the value of the loss function and any additional metrics at the end of each epoch. These operations are controlled by the methods SimpleModule.[training/test/validation]_step(), though we will not be modifying these in our examples.
25This depends on the computing hardware and the number of cores available.
In [25]: hit_module = SimpleModule.regression(hit_model,
metrics={'mae':MeanAbsoluteError()})By using the SimpleModule.regression() method, we indicate that we SimpleModule. will use squared-error loss as in ( regression() 10.23). We have also asked for mean absolute error to be tracked as well in the metrics that are logged.
We log our results via CSVLogger(), which in this case stores the results in a CSV fle within a directory logs/hitters. After the ftting is complete, this allows us to load the results as a pd.DataFrame() and visualize them below. There are several ways to log the results within pytorch_lightning, though we will not cover those here in detail.
In [26]: hit_logger = CSVLogger('logs', name='hitters')Finally we are ready to train our model and log the results. We use the Trainer() object from pytorch_lightning to do this work. The argument datamodule=hit_dm tells the trainer how training/validation/test logs are produced, while the frst argument hit_module specifes the network architecture as well as the training/validation/test steps. The callbacks argument allows for several tasks to be carried out at various points while training a model. Here our ErrorTracker() callback will enable us to compute validation error while training and, fnally, the test error. We now ft the model for 50 epochs.
In [27]: hit_trainer = Trainer(deterministic=True,
max_epochs=50,
log_every_n_steps=5,
logger=hit_logger,
callbacks=[ErrorTracker()])
hit_trainer.fit(hit_module, datamodule=hit_dm)At each step of SGD, the algorithm randomly selects 32 training observations for the computation of the gradient. Recall from Section 10.7 that an epoch amounts to the number of SGD steps required to process n observations. Since the training set has n = 175, and we specifed a batch_size of 32 in the construction of hit_dm, an epoch is 175/32 = 5.5 SGD steps.
After having ft the model, we can evaluate performance on our test data using the test() method of our trainer.
In [28]: hit_trainer.test(hit_module, datamodule=hit_dm)Out[28]: [{'test_loss': 104098.5469, 'test_mae': 229.5012}]The results of the ft have been logged into a CSV fle. We can fnd the results specifc to this run in the experiment.metrics_file_path attribute of our logger. Note that each time the model is ft, the logger will output results into a new subdirectory of our directory logs/hitters.
We now create a plot of the MAE (mean absolute error) as a function of the number of epochs. First we retrieve the logged summaries.
hit_results = pd.read_csv(hit_logger.experiment.metrics_file_path)Since we will produce similar plots in later examples, we write a simple generic function to produce this plot.
In [29]: def summary_plot(results,
ax,
col='loss',
valid_legend='Validation',
training_legend='Training',
ylabel='Loss',
fontsize=20):
for (column,
color,
label) in zip([f'train_{col}_epoch',
f'valid_{col}'],
['black',
'red'],
[training_legend,
valid_legend]):
results.plot(x='epoch',
y=column,
label=label,
marker='o',
color=color,
ax=ax)
ax.set_xlabel('Epoch')
ax.set_ylabel(ylabel)
return axWe now set up our axes, and use our function to produce the MAE plot.
In [30]: fig, ax = subplots(1, 1, figsize=(6, 6))
ax = summary_plot(hit_results,
ax,
col='mae',
ylabel='MAE',
valid_legend='Validation (=Test)')
ax.set_ylim([0, 400])
ax.set_xticks(np.linspace(0, 50, 11).astype(int));We can predict directly from the fnal model, and evaluate its performance on the test data. Before ftting, we call the eval() method of hit_model. This tells torch to efectively consider this model to be ftted, so that we can use it to predict on new data. For our model here, the biggest change is that the dropout layers will be turned of, i.e. no weights will be randomly dropped in predicting on new data.
In [31]: hit_model.eval()
preds = hit_module(X_test_t)
torch.abs(Y_test_t - preds).mean()Out[31]: tensor(229.5012, grad_fn=
Cleanup
In setting up our data module, we had initiated several worker processes that will remain running. We delete all references to the torch objects to ensure these processes will be killed.
444 10. Deep Learning
In [32]: del(Hitters, hit_model, hit_dm, hit_logger, hit_test, hit_train, X, Y, X_test, X_train, Y_test, Y_train, X_test_t, Y_test_t, hit_trainer, hit_module)
10.9.2 Multilayer Network on the MNIST Digit Data
The torchvision package comes with a number of example datasets, including the MNIST digit data. Our frst step is to retrieve the training and test data sets; the MNIST() function within torchvision.datasets is provided for MNIST() this purpose. The data will be downloaded the frst time this function is executed, and stored in the directory data/MNIST.
In [33]: (mnist_train,mnist_test) = [MNIST(root='data',
train=train,
download=True,
transform=ToTensor())
for train in [True, False]]
mnist_trainOut[33]: Dataset MNIST
Number of datapoints: 60000
Root location: data
Split: Train
StandardTransform
Transform: ToTensor()There are 60,000 images in the training data and 10,000 in the test data. The images are 28 × 28, and stored as a matrix of pixels. We need to transform each one into a vector.
Neural networks are somewhat sensitive to the scale of the inputs, much as ridge and lasso regularization are afected by scaling. Here the inputs are eight-bit grayscale values between 0 and 255, so we rescale to the unit interval.26 This transformation, along with some reordering of the axes, is performed by the ToTensor() transform from the torchvision.transforms package.
As in our Hitters example, we form a data module from the training and test datasets, setting aside 20% of the training images for validation.
In [34]: mnist_dm = SimpleDataModule(mnist_train,
mnist_test,
validation=0.2,
num_workers=max_num_workers,
batch_size=256)26Note: eight bits means 28, which equals 256. Since the convention is to start at 0, the possible values range from 0 to 255.
Let’s take a look at the data that will get fed into our network. We loop through the frst few chunks of the test dataset, breaking after 2 batches:
In [35]: for idx, (X_ ,Y_) in enumerate(mnist_dm.train_dataloader()):
print('X: ', X_.shape)
print('Y: ', Y_.shape)
if idx >= 1:
break
X: torch.Size([256, 1, 28, 28])
Y: torch.Size([256])X: torch.Size([256, 1, 28, 28])
Y: torch.Size([256])We see that the X for each batch consists of 256 images of size 1x28x28. Here the 1 indicates a single channel (greyscale). For RGB images such as CIFAR100 below, we will see that the 1 in the size will be replaced by 3 for the three RGB channels.
Now we are ready to specify our neural network.
In [36]: class MNISTModel(nn.Module):def __init__(self):
super(MNISTModel, self).__init__()
self.layer1 = nn.Sequential(
nn.Flatten(),
nn.Linear(28*28, 256),
nn.ReLU(),
nn.Dropout(0.4))
self.layer2 = nn.Sequential(
nn.Linear(256, 128),
nn.ReLU(),
nn.Dropout(0.3))
self._forward = nn.Sequential(
self.layer1,
self.layer2,
nn.Linear(128, 10))
def forward(self, x):
return self._forward(x)We see that in the frst layer, each 1x28x28 image is fattened, then mapped to 256 dimensions where we apply a ReLU activation with 40% dropout. A second layer maps the frst layer’s output down to 128 dimensions, applying a ReLU activation with 30% dropout. Finally, the 128 dimensions are mapped down to 10, the number of classes in the MNIST data.
In [37]: mnist_model = MNISTModel()We can check that the model produces output of expected size based on our existing batch X_ above.
In [38]: mnist_model(X_).size()Out[38]: torch.Size([256, 10])Let’s take a look at the summary of the model. Instead of an input_size we can pass a tensor of correct shape. In this case, we pass through the fnal batched X_ from above.
446 10. Deep Learning
In [39]: summary(mnist_model,
input_data=X_,
col_names=['input_size',
'output_size',
'num_params'])| Layer | (type:depth-idx) | Input | Shape | Output Shape |
Param # |
|---|---|---|---|---|---|
| MNISTModel | ===================================================================== | [256, | 1, 28, 28] |
[256, 10] |
– |
| Sequential: 1-1 |
[256, | 1, 28, 28] |
[256, 10] |
– | |
| Sequential: 2-1 |
[256, | 1, 28, 28] |
[256, 256] |
– | |
| Flatten: 3-1 |
[256, | 1, 28, 28] |
[256, 784] |
– | |
| Linear: 3-2 |
[256, | 784] | [256, 256] |
200,960 | |
| ReLU: 3-3 |
[256, | 256] | [256, 256] |
– | |
| Dropout: 3-4 |
[256, | 256] | [256, 256] |
– | |
| Sequential: 2-2 |
[256, | 256] | [256, 128] |
– | |
| Linear: 3-5 |
[256, | 256] | [256, 128] |
32,896 | |
| ReLU: 3-6 |
[256, | 128] | [256, 128] |
– | |
| Dropout: 3-7 |
[256, | 128] | [256, 128] |
– | |
| Linear: 2-3 |
[256, | 128] | [256, 10] |
1,290 |
Having set up both the model and the data module, ftting this model is now almost identical to the Hitters example. In contrast to our regression model, here we will use the SimpleModule.classification() method which SimpleModule. uses the cross-entropy loss function instead of mean squared error.
classification()
In [40]: mnist_module = SimpleModule.classification(mnist_model)
mnist_logger = CSVLogger('logs', name='MNIST')Now we are ready to go. The fnal step is to supply training data, and ft the model.
In [41]: mnist_trainer = Trainer(deterministic=True,
max_epochs=30,
logger=mnist_logger,
callbacks=[ErrorTracker()])
mnist_trainer.fit(mnist_module,
datamodule=mnist_dm)We have suppressed the output here, which is a progress report on the ftting of the model, grouped by epoch. This is very useful, since on large datasets ftting can take time. Fitting this model took 245 seconds on a MacBook Pro with an Apple M1 Pro chip with 10 cores and 16 GB of RAM. Here we specifed a validation split of 20%, so training is actually performed on 80% of the 60,000 observations in the training set. This is an alternative to actually supplying validation data, like we did for the Hitters data. SGD uses batches of 256 observations in computing the gradient, and doing the arithmetic, we see that an epoch corresponds to 188 gradient steps.
SimpleModule.classification() includes an accuracy metric by default. Other classifcation metrics can be added from torchmetrics. We will use our summary_plot() function to display accuracy across epochs.
In [42]: mnist_results = pd.read_csv(mnist_logger.experiment.
metrics_file_path)
fig, ax = subplots(1, 1, figsize=(6, 6))
summary_plot(mnist_results,
ax,
col='accuracy',
ylabel='Accuracy')
ax.set_ylim([0.5, 1])
ax.set_ylabel('Accuracy')
ax.set_xticks(np.linspace(0, 30, 7).astype(int));Once again we evaluate the accuracy using the test() method of our trainer. This model achieves 97% accuracy on the test data.
In [43]: mnist_trainer.test(mnist_module,
datamodule=mnist_dm)Out[43]: [{‘test_loss’: 0.1471, ‘test_accuracy’: 0.9681}]
Table 10.1 also reports the error rates resulting from LDA (Chapter 4) and multiclass logistic regression. For LDA we refer the reader to Section 4.7.3. Although we could use the sklearn function LogisticRegression() to ft multiclass logistic regression, we are set up here to ft such a model with torch. We just have an input layer and an output layer, and omit the hidden layers!
In [44]: class MNIST_MLR(nn.Module):
def __init__(self):
super(MNIST_MLR, self).__init__()
self.linear = nn.Sequential(nn.Flatten(),
nn.Linear(784, 10))
def forward(self, x):
return self.linear(x)
mlr_model = MNIST_MLR()
mlr_module = SimpleModule.classification(mlr_model)
mlr_logger = CSVLogger('logs', name='MNIST_MLR')In [45]: mlr_trainer = Trainer(deterministic=True,
max_epochs=30,
callbacks=[ErrorTracker()])
mlr_trainer.fit(mlr_module, datamodule=mnist_dm)We ft the model just as before and compute the test results.
In [46]: mlr_trainer.test(mlr_module,
datamodule=mnist_dm)Out[46]: [{'test_loss': 0.3187, 'test_accuracy': 0.9241}]The accuracy is above 90% even for this pretty simple model.
As in the Hitters example, we delete some of the objects we created above.
In [47]: del(mnist_test, mnist_train, 448 10. Deep Learning
mnist_model,
mnist_dm,
mnist_trainer,
mnist_module,
mnist_results,
mlr_model,
mlr_module,
mlr_trainer)10.9.3 Convolutional Neural Networks
In this section we ft a CNN to the CIFAR100 data, which is available in the torchvision package. It is arranged in a similar fashion as the MNIST data.
In [48]: (cifar_train,
cifar_test) = [CIFAR100(root="data",
train=train,
download=True)
for train in [True, False]]In [49]: transform = ToTensor()
cifar_train_X = torch.stack([transform(x) for x in
cifar_train.data])
cifar_test_X = torch.stack([transform(x) for x in
cifar_test.data])
cifar_train = TensorDataset(cifar_train_X,
torch.tensor(cifar_train.targets))
cifar_test = TensorDataset(cifar_test_X,
torch.tensor(cifar_test.targets))The CIFAR100 dataset consists of 50,000 training images, each represented by a three-dimensional tensor: each three-color image is represented as a set of three channels, each of which consists of 32 × 32 eight-bit pixels. We standardize as we did for the digits, but keep the array structure. This is accomplished with the ToTensor() transform.
Creating the data module is similar to the MNIST example.
In [50]: cifar_dm = SimpleDataModule(cifar_train,
cifar_test,
validation=0.2,
num_workers=max_num_workers,
batch_size=128)We again look at the shape of typical batches in our data loaders.
In [51]: for idx, (X_ ,Y_) in enumerate(cifar_dm.train_dataloader()): print(‘X:’, X_.shape) print(‘Y:’, Y_.shape) if idx >= 1: break
X: torch.Size([128, 3, 32, 32])
Y: torch.Size([128])
X: torch.Size([128, 3, 32, 32])
Y: torch.Size([128])Before we start, we look at some of the training images; similar code produced Figure 10.5 on page 406. The example below also illustrates that TensorDataset objects can be indexed with integers — we are choosing random images from the training data by indexing cifar_train. In order to display correctly, we must reorder the dimensions by a call to np.transpose().
In [52]: fig, axes = subplots(5, 5, figsize=(10,10))
rng = np.random.default_rng(4)
indices = rng.choice(np.arange(len(cifar_train)), 25,
replace=False).reshape((5,5))
for i in range(5):
for j in range(5):
idx = indices[i,j]
axes[i,j].imshow(np.transpose(cifar_train[idx][0],
[1,2,0]),
interpolation=None)
axes[i,j].set_xticks([])
axes[i,j].set_yticks([])Here the imshow() method recognizes from the shape of its argument that .imshow() it is a 3-dimensional array, with the last dimension indexing the three RGB color channels.
We specify a moderately-sized CNN for demonstration purposes, similar in structure to Figure 10.8. We use several layers, each consisting of convolution, ReLU, and max-pooling steps. We frst defne a module that defnes one of these layers. As in our previous examples, we overwrite the __init__() and forward() methods of nn.Module. This user-defned module can now be used in ways just like nn.Linear() or nn.Dropout().
In [53]: class BuildingBlock(nn.Module):
def __init__(self,in_channels,
out_channels):
super(BuildingBlock , self).__init__()
self.conv = nn.Conv2d(in_channels=in_channels,
out_channels=out_channels,
kernel_size=(3,3),
padding='same')
self.activation = nn.ReLU()
self.pool = nn.MaxPool2d(kernel_size=(2,2))
def forward(self, x):
return self.pool(self.activation(self.conv(x)))Notice that we used the padding = “same” argument to nn.Conv2d(), which ensures that the output channels have the same dimension as the input channels. There are 32 channels in the frst hidden layer, in contrast to the three channels in the input layer. We use a 3 × 3 convolution flter for each channel in all the layers. Each convolution is followed by a max-pooling layer over 2 × 2 blocks.
In forming our deep learning model for the CIFAR100 data, we use several of our BuildingBlock() modules sequentially. This simple example illustrates some of the power of torch. Users can defne modules of their own, which can be combined in other modules. Ultimately, everything is ft by a generic trainer.
In [54]: class CIFARModel(nn.Module):
def __init__(self):
super(CIFARModel, self).__init__()
sizes = [(3,32),
(32,64),
(64,128),
(128,256)]
self.conv = nn.Sequential(*[BuildingBlock(in_, out_)
for in_, out_ in sizes])
self.output = nn.Sequential(nn.Dropout(0.5),
nn.Linear(2*2*256, 512),
nn.ReLU(),
nn.Linear(512, 100))
def forward(self, x):
val = self.conv(x)
val = torch.flatten(val, start_dim=1)
return self.output(val)We build the model and look at the summary. (We had created examples of X_ earlier.)
In [55]: cifar_model = CIFARModel()
summary(cifar_model,
input_data=X_,
col_names=['input_size',
'output_size',
'num_params'])| Out[55]: ====================================================================== | |||
|---|---|---|---|
| Layer (type:depth-idx) |
Input Shape |
Output Shape |
Param # |
| ====================================================================== CIFARModel |
[128, 3, 32, 32] |
[128, 100] |
– |
| Sequential: 1-1 |
[128, 3, 32, 32] |
[128, 256, 2, 2] |
– |
| BuildingBlock: 2-1 |
[128, 3, 32, 32] |
[128, 32, 16, 16] |
– |
| Conv2d: 3-1 |
[128, 3, 32, 32] |
[128, 32, 32, 32] |
896 |
| ReLU: 3-2 |
[128, 32, 32, 32] |
[128, 32, 32, 32] |
– |
| MaxPool2d: 3-3 |
[128, 32, 32, 32] |
[128, 32, 16, 16] |
– |
| BuildingBlock: 2-2 |
[128, 32, 16, 16] |
[128, 64, 8, 8] |
– |
| Conv2d: 3-4 |
[128, 32, 16, 16] |
[128, 64, 16, 16] |
18,496 |
| ReLU: 3-5 |
[128, 64, 16, 16] |
[128, 64, 16, 16] |
– |
| MaxPool2d: 3-6 |
[128, 64, 16, 16] |
[128, 64, 8, 8] |
– |
| BuildingBlock: 2-3 |
[128, 64, 8, 8] |
[128, 128, 4, 4] |
– |
| Conv2d: 3-7 |
[128, 64, 8, 8] |
[128, 128, 8, 8] |
73,856 |
| ReLU: 3-8 |
[128, 128, 8, 8] |
[128, 128, 8, 8] |
– |
| MaxPool2d: 3-9 |
[128, 128, 8, 8] |
[128, 128, 4, 4] |
– |
| BuildingBlock: 2-4 |
[128, 128, 4, 4] |
[128, 256, 2, 2] |
– |
| Conv2d: 3-10 |
[128, 128, 4, 4] |
[128, 256, 4, 4] |
295,168 |
| ReLU: 3-11 |
[128, 256, 4, 4] |
[128, 256, 4, 4] |
– |
| MaxPool2d: 3-12 |
[128, 256, 4, 4] |
[128, 256, 2, 2] |
– |
| Sequential: 1-2 |
[128, 1024] |
[128, 100] |
– |
| Dropout: 2-5 |
[128, 1024] |
[128, 1024] |
– |
| Linear: 2-6 |
[128, 1024] |
[128, 512] |
524,800 |
| ====================================================================== | |||
|---|---|---|---|
| Linear: | [128, | [128, | 51,300 |
| 2-8 | 512] | 100] | |
| ReLU: | [128, | [128, | – |
| 2-7 | 512] | 512] |
Total params: 964,516 Trainable params: 964,516
The total number of trainable parameters is 964,516. By studying the size of the parameters, we can see that the channels halve in both dimensions after each of these max-pooling operations. After the last of these we have a layer with 256 channels of dimension 2 × 2. These are then fattened to a dense layer of size 1,024; in other words, each of the 2 × 2 matrices is turned into a 4-vector, and put side-by-side in one layer. This is followed by a dropout regularization layer, then another dense layer of size 512, and fnally, the output layer.
Up to now, we have been using a default optimizer in SimpleModule(). For these data, experiments show that a smaller learning rate performs better than the default 0.01. We use a custom optimizer here with a learning rate of 0.001. Besides this, the logging and training follow a similar pattern to our previous examples. The optimizer takes an argument params that informs the optimizer which parameters are involved in SGD (stochastic gradient descent).
We saw earlier that entries of a module’s parameters are tensors. In passing the parameters to the optimizer we are doing more than simply passing arrays; part of the structure of the graph is encoded in the tensors themselves.
In [56]: cifar_optimizer = RMSprop(cifar_model.parameters(), lr=0.001)
cifar_module = SimpleModule.classification(cifar_model,
optimizer=cifar_optimizer)
cifar_logger = CSVLogger('logs', name='CIFAR100')In [57]: cifar_trainer = Trainer(deterministic=True,
max_epochs=30,
logger=cifar_logger,
callbacks=[ErrorTracker()])
cifar_trainer.fit(cifar_module,
datamodule=cifar_dm)This model takes 10 minutes or more to run and achieves about 42% accuracy on the test data. Although this is not terrible for 100-class data (a random classifer gets 1% accuracy), searching the web we see results around 75%. Typically it takes a lot of architecture carpentry, fddling with regularization, and time, to achieve such results.
Let’s take a look at the validation and training accuracy across epochs.
In [58]: log_path = cifar_logger.experiment.metrics_file_path cifar_results = pd.read_csv(log_path) fig, ax = subplots(1, 1, figsize=(6, 6)) summary_plot(cifar_results, ax, col=‘accuracy’, ylabel=‘Accuracy’) ax.set_xticks(np.linspace(0, 10, 6).astype(int)) ax.set_ylabel(‘Accuracy’) ax.set_ylim([0, 1]);
452 10. Deep Learning
Finally, we evaluate our model on our test data.
In [59]: cifar_trainer.test(cifar_module,
datamodule=cifar_dm)Out[59]: [{‘test_loss’: 2.4238 ‘test_accuracy’: 0.4206}]
Hardware Acceleration
As deep learning has become ubiquitous in machine learning, hardware manufacturers have produced special libraries that can often speed up the gradient-descent steps.
For instance, Mac OS devices with the M1 chip may have the Metal programming framework enabled, which can speed up the torch computations. We present an example of how to use this acceleration.
The main changes are to the Trainer() call as well as to the metrics that will be evaluated on the data. These metrics must be told where the data will be located at evaluation time. This is accomplished with a call to the to() method of the metrics.
In [60]: try:for name, metric in cifar_module.metrics.items():
cifar_module.metrics[name] = metric.to('mps')
cifar_trainer_mps = Trainer(accelerator='mps',
deterministic=True,
max_epochs=30)
cifar_trainer_mps.fit(cifar_module,
datamodule=cifar_dm)
cifar_trainer_mps.test(cifar_module,
datamodule=cifar_dm)
except:
passThis yields approximately two- or three-fold acceleration for each epoch. We have protected this code block using try: and except: clauses; if it works, we get the speedup, if it fails, nothing happens.
10.9.4 Using Pretrained CNN Models
We now show how to use a CNN pretrained on the imagenet database to classify natural images, and demonstrate how we produced Figure 10.10. We copied six JPEG images from a digital photo album into the directory book_images. These images are available from the data section of www. statlearning.com, the ISLP book website. Download book_images.zip; when clicked it creates the book_images directory.
The pretrained network we use is called resnet50; specifcation details can be found on the web. We will read in the images, and convert them into the array format expected by the torch software to match the specifcations in resnet50. The conversion involves a resize, a crop and then a predefned standardization for each of the three channels. We now read in the images and preprocess them.
In [61]: resize = Resize((232,232))
crop = CenterCrop(224)
normalize = Normalize([0.485,0.456,0.406],
[0.229,0.224,0.225])
imgfiles = sorted([f for f in glob('book_images/*')])
imgs = torch.stack([torch.div(crop(resize(read_image(f))), 255)
for f in imgfiles])
imgs = normalize(imgs)
imgs.size()Out[61]: torch.Size([6, 3, 224, 224])
We now set up the trained network with the weights we read in code block 6. The model has 50 layers, with a fair bit of complexity.
In [62]: resnet_model = resnet50(weights=ResNet50_Weights.DEFAULT)
summary(resnet_model,
input_data=imgs,
col_names=['input_size',
'output_size',
'num_params'])We set the mode to eval() to ensure that the model is ready to predict on new data.
In [63]: resnet_model.eval()Inspecting the output above, we see that when setting up the resnet_model, the authors defned a Bottleneck, much like our BuildingBlock module. We now feed our six images through the ftted network.
In [64]: img_preds = resnet_model(imgs)
Let’s look at the predicted probabilities for each of the top 3 choices. First we compute the probabilities by applying the softmax to the logits in img_preds. Note that we have had to call the detach() method on the tensor img_preds in order to convert it to our a more familiar ndarray.
In [65]: img_probs = np.exp(np.asarray(img_preds.detach()))
img_probs /= img_probs.sum(1)[:,None]In order to see the class labels, we must download the index fle associated with imagenet. 27
In [66]: labs = json.load(open('imagenet_class_index.json'))
class_labels = pd.DataFrame([(int(k), v[1]) for k, v in
labs.items()],
columns=['idx', 'label'])
class_labels = class_labels.set_index('idx')
class_labels = class_labels.sort_index()We’ll now construct a data frame for each image fle with the labels with the three highest probabilities as estimated by the model above.
27This is avalable from the book website and s3.amazonaws.com/deep-learningmodels/image-models/imagenet\_class\_index.json.
454 10. Deep Learning
In [67]: for i, imgfile in enumerate(imgfiles):
img_df = class_labels.copy()
img_df['prob'] = img_probs[i]
img_df = img_df.sort_values(by='prob', ascending=False)[:3]
print(f'Image: {imgfile}')
print(img_df.reset_index().drop(columns=['idx']))
Image: book_images/Cape_Weaver.jpg
label prob
0 jacamar 0.287283
1 bee_eater 0.046768
2 bulbul 0.037507
Image: book_images/Flamingo.jpg
label prob
0 flamingo 0.591761
1 spoonbill 0.012386
2 American_egret 0.002105
Image: book_images/Hawk_Fountain.jpg
label prob
0 great_grey_owl 0.287959
1 kite 0.039478
2 fountain 0.029384
Image: book_images/Hawk_cropped.jpg
label prob
0 kite 0.301830
1 jay 0.121674
2 magpie 0.015513
Image: book_images/Lhasa_Apso.jpg
label prob
0 Lhasa 0.151143
1 Shih-Tzu 0.129850
2 Tibetan_terrier 0.102358
Image: book_images/Sleeping_Cat.jpg
label prob
0 tabby 0.173627
1 tiger_cat 0.110414
2 doormat 0.093447We see that the model is quite confdent about Flamingo.jpg, but a little less so for the other images.
We end this section with our usual cleanup.
In [68]: del(cifar_test,
cifar_train,
cifar_dm,
cifar_module,
cifar_logger,
cifar_optimizer,cifar_trainer)
10.9.5 IMDB Document Classifcation
We now implement models for sentiment classifcation (Section 10.4) on the IMDB dataset. As mentioned above code block 8, we are using a preprocessed version of the IMDB dataset found in the keras package. As keras uses tensorflow, a diferent tensor and deep learning library, we have converted the data to be suitable for torch. The code used to convert from keras is available in the module ISLP.torch._make_imdb. It requires some of the keras packages to run. These data use a dictionary of size 10,000.
We have stored three diferent representations of the review data for this lab:
- load_tensor(), a sparse tensor version usable by torch;
- load_sparse(), a sparse matrix version usable by sklearn, since we will compare with a lasso ft;
- load_sequential(), a padded version of the original sequence representation, limited to the last 500 words of each review.
In [69]: (imdb_seq_train,imdb_seq_test) = load_sequential(root='data/IMDB')
padded_sample = np.asarray(imdb_seq_train.tensors[0][0])
sample_review = padded_sample[padded_sample > 0][:12]
sample_review[:12]Out[69]: array([ 1, 14, 22, 16, 43, 530, 973, 1622, 1385,
65, 458, 4468], dtype=int32)The datasets imdb_seq_train and imdb_seq_test are both instances of the class TensorDataset. The tensors used to construct them can be found in the tensors attribute, with the frst tensor the features X and the second the outcome Y. We have taken the frst row of features and stored it as padded_sample. In the preprocessing used to form these data, sequences were padded with 0s in the beginning if they were not long enough, hence we remove this padding by restricting to entries where padded_sample > 0. We then provide the frst 12 words of the sample review.
We can fnd these words in the lookup dictionary from the ISLP.torch.imdb module.
In [70]: lookup = load_lookup(root='data/IMDB')
' '.join(lookup[i] for i in sample_review)Out[70]: “ this film was just brilliant casting location scenery story direction everyone’s”
For our frst model, we have created a binary feature for each of the 10,000 possible words in the dataset, with an entry of one in the i, j entry if word j appears in review i. As most reviews are quite short, such a feature matrix has over 98% zeros. These data are accessed using load_tensor() from the ISLP library.
In [71]: max_num_workers=10
(imdb_train,
imdb_test) = load_tensor(root='data/IMDB')
imdb_dm = SimpleDataModule(imdb_train,
imdb_test,
validation=2000,
num_workers=min(6, max_num_workers),
batch_size=512)456 10. Deep Learning
We’ll use a two-layer model for our frst model.
In [72]: class IMDBModel(nn.Module):
def __init__(self, input_size):
super(IMDBModel, self).__init__()
self.dense1 = nn.Linear(input_size, 16)
self.activation = nn.ReLU()
self.dense2 = nn.Linear(16, 16)
self.output = nn.Linear(16, 1)
def forward(self, x):
val = x
for _map in [self.dense1,
self.activation,
self.dense2,
self.activation,
self.output]:
val = _map(val)
return torch.flatten(val)We now instantiate our model and look at a summary (not shown).
In [73]: imdb_model = IMDBModel(imdb_test.tensors[0].size()[1])
summary(imdb_model,
input_size=imdb_test.tensors[0].size(),
col_names=['input_size',
'output_size',
'num_params'])We’ll again use a smaller learning rate for these data, hence we pass an optimizer to the SimpleModule. Since the reviews are classifed into positive or negative sentiment, we use SimpleModule.binary_classification(). 28
In [74]: imdb_optimizer = RMSprop(imdb_model.parameters(), lr=0.001)
imdb_module = SimpleModule.binary_classification(
imdb_model,
optimizer=imdb_optimizer)Having loaded the datasets into a data module and created a SimpleModule, the remaining steps are familiar.
In [75]: imdb_logger = CSVLogger('logs', name='IMDB')
imdb_trainer = Trainer(deterministic=True,
max_epochs=30,
logger=imdb_logger,
callbacks=[ErrorTracker()])
imdb_trainer.fit(imdb_module,
datamodule=imdb_dm)Evaluating the test error yields roughly 86% accuracy.
In [76]: test_results = imdb_trainer.test(imdb_module, datamodule=imdb_dm)
test_results28Our use of binary_classification() instead of classification() is due to some subtlety in how torchmetrics.Accuracy() works, as well as the data type of the targets.
Out[76]: [{'test_loss': 1.0863, 'test_accuracy': 0.8550}]Comparison to Lasso
We now ft a lasso logistic regression model using LogisticRegression() from sklearn. Since sklearn does not recognize the sparse tensors of torch, we use a sparse matrix that is recognized by sklearn.
In [77]: ((X_train, Y_train),
(X_valid, Y_valid),
(X_test, Y_test)) = load_sparse(validation=2000,
random_state=0,
root='data/IMDB')Similar to what we did in Section 10.9.1, we construct a series of 50 values for the lasso reguralization parameter λ.
In [78]: lam_max = np.abs(X_train.T * (Y_train - Y_train.mean())).max()
lam_val = lam_max * np.exp(np.linspace(np.log(1),
np.log(1e-4), 50))With LogisticRegression() the regularization parameter C is specifed as the inverse of λ. There are several solvers for logistic regression; here we use liblinear which works well with the sparse input format.
In [79]: logit = LogisticRegression(penalty='l1',
C=1/lam_max,
solver='liblinear',
warm_start=True,
fit_intercept=True)The path of 50 values takes approximately 40 seconds to run.
In [80]: coefs = []
intercepts = []
for l in lam_val:
logit.C = 1/l
logit.fit(X_train, Y_train)
coefs.append(logit.coef_.copy())
intercepts.append(logit.intercept_)The coefcient and intercepts have an extraneous dimension which can be removed by the np.squeeze() function.
In [81]: coefs = np.squeeze(coefs)
intercepts = np.squeeze(intercepts)We’ll now make a plot to compare our neural network results with the lasso.
In [82]: %%capture
fig, axes = subplots(1, 2, figsize=(16, 8), sharey=True)
for ((X_, Y_),
data_,
color) in zip([(X_train, Y_train),
(X_valid, Y_valid),
(X_test, Y_test)],458 10. Deep Learning
['Training', 'Validation', 'Test'],
['black', 'red', 'blue']):
linpred_ = X_ * coefs.T + intercepts[None,:]
label_ = np.array(linpred_ > 0)
accuracy_ = np.array([np.mean(Y_ == l) for l in label_.T])
axes[0].plot(-np.log(lam_val / X_train.shape[0]),
accuracy_,
'.--',
color=color,
markersize=13,
linewidth=2,
label=data_)
axes[0].legend()
axes[0].set_xlabel(r'$-\log(\lambda)$', fontsize=20)
axes[0].set_ylabel('Accuracy', fontsize=20)Notice the use of %%capture, which suppresses the displaying of the partially %%capture completed fgure. This is useful when making a complex fgure, since the steps can be spread across two or more cells. We now add a plot of the lasso accuracy, and display the composed fgure by simply entering its name at the end of the cell.
In [83]: imdb_results = pd.read_csv(imdb_logger.experiment.metrics_file_path)
summary_plot(imdb_results,
axes[1],
col='accuracy',
ylabel='Accuracy')
axes[1].set_xticks(np.linspace(0, 30, 7).astype(int))
axes[1].set_ylabel('Accuracy', fontsize=20)
axes[1].set_xlabel('Epoch', fontsize=20)
axes[1].set_ylim([0.5, 1]);
axes[1].axhline(test_results[0]['test_accuracy'],
color='blue',
linestyle='--',
linewidth=3)
figFrom the graphs we see that the accuracy of the lasso logistic regression peaks at about 0.88, as it does for the neural network.
Once again, we end with a cleanup.
In [84]: del(imdb_model,
imdb_trainer,
imdb_logger,
imdb_dm,imdb_train,imdb_test)10.9.6 Recurrent Neural Networks
In this lab we ft the models illustrated in Section 10.5.
Sequential Models for Document Classifcation
Here we ft a simple LSTM RNN for sentiment prediction to the IMDb movie-review data, as discussed in Section 10.5.1. For an RNN we use
the sequence of words in a document, taking their order into account. We loaded the preprocessed data at the beginning of Section 10.9.5. A script that details the preprocessing can be found in the ISLP library. Notably, since more than 90% of the documents had fewer than 500 words, we set the document length to 500. For longer documents, we used the last 500 words, and for shorter documents, we padded the front with blanks.
In [85]: imdb_seq_dm = SimpleDataModule(imdb_seq_train,
imdb_seq_test,
validation=2000,
batch_size=300,
num_workers=min(6, max_num_workers)
)The frst layer of the RNN is an embedding layer of size 32, which will be learned during training. This layer one-hot encodes each document as a matrix of dimension 500×10, 003, and then maps these 10, 003 dimensions down to 32. 29 Since each word is represented by an integer, this is efectively achieved by the creation of an embedding matrix of size 10, 003 × 32; each of the 500 integers in the document are then mapped to the appropriate 32 real numbers by indexing the appropriate rows of this matrix.
The second layer is an LSTM with 32 units, and the output layer is a single logit for the binary classifcation task. In the last line of the forward() method below, we take the last 32-dimensional output of the LSTM and map it to our response.
In [86]: class LSTMModel(nn.Module):
def __init__(self, input_size):
super(LSTMModel, self).__init__()
self.embedding = nn.Embedding(input_size, 32)
self.lstm = nn.LSTM(input_size=32,
hidden_size=32,
batch_first=True)
self.dense = nn.Linear(32, 1)
def forward(self, x):
val, (h_n, c_n) = self.lstm(self.embedding(x))
return torch.flatten(self.dense(val[:,-1]))We instantiate and take a look at the summary of the model, using the frst 10 documents in the corpus.
In [87]: lstm_model = LSTMModel(X_test.shape[-1])
summary(lstm_model,
input_data=imdb_seq_train.tensors[0][:10],
col_names=['input_size',
'output_size',
'num_params'])Out[87]: ====================================================================
Layer (type:depth-idx) Input Shape Output Shape Param #
====================================================================
LSTMModel [10, 500] [10] --29The extra 3 dimensions correspond to commonly occurring non-word entries in the reviews.
460 10. Deep Learning
Embedding: 1-1 [10, 500] [10, 500, 32] 320,096 LSTM: 1-2 [10, 500, 32] [10, 500, 32] 8,448 Linear: 1-3 [10, 32] [10, 1] 33 ==================================================================== Total params: 328,577
Trainable params: 328,577
The 10,003 is suppressed in the summary, but we see it in the parameter count, since 10, 003 × 32 = 320, 096.
In [88]: lstm_module = SimpleModule.binary_classification(lstm_model)
lstm_logger = CSVLogger('logs', name='IMDB_LSTM')In [89]: lstm_trainer = Trainer(deterministic=True,
max_epochs=20,
logger=lstm_logger,
callbacks=[ErrorTracker()])
lstm_trainer.fit(lstm_module,
datamodule=imdb_seq_dm)The rest is now similar to other networks we have ft. We track the test performance as the network is ft, and see that it attains 85% accuracy.
In [90]: lstm_trainer.test(lstm_module, datamodule=imdb_seq_dm)
Out[90]: [{'test_loss': 0.8178, 'test_accuracy': 0.8476}]We once again show the learning progress, followed by cleanup.
In [91]: lstm_results = pd.read_csv(lstm_logger.experiment.metrics_file_path)
fig, ax = subplots(1, 1, figsize=(6, 6))
summary_plot(lstm_results,
ax,
col='accuracy',
ylabel='Accuracy')
ax.set_xticks(np.linspace(0, 20, 5).astype(int))
ax.set_ylabel('Accuracy')
ax.set_ylim([0.5, 1])In [92]: del(lstm_model,
lstm_trainer, lstm_logger, imdb_seq_dm, imdb_seq_train, imdb_seq_test)
Time Series Prediction
We now show how to ft the models in Section 10.5.2 for time series prediction. We frst load and standardize the data.
In [93]: NYSE = load_data('NYSE')
cols = ['DJ_return', 'log_volume', 'log_volatility']
X = pd.DataFrame(StandardScaler(
with_mean=True,
with_std=True).fit_transform(NYSE[cols]),
columns=NYSE[cols].columns,
index=NYSE.index)Next we set up the lagged versions of the data, dropping any rows with missing values using the dropna() method.
In [94]: for lag in range(1, 6):
for col in cols:
newcol = np.zeros(X.shape[0]) * np.nan
newcol[lag:] = X[col].values[:-lag]
X.insert(len(X.columns), "{0}_{1}".format(col, lag), newcol)
X.insert(len(X.columns), 'train', NYSE['train'])
X = X.dropna()Finally, we extract the response, training indicator, and drop the current day’s DJ_return and log_volatility to predict only from previous day’s data.
In [95]: Y, train = X[‘log_volume’], X[‘train’] X = X.drop(columns=[‘train’] + cols) X.columns
Out[95]: Index(['DJ_return_1', 'log_volume_1', 'log_volatility_1',
'DJ_return_2', 'log_volume_2', 'log_volatility_2',
'DJ_return_3', 'log_volume_3', 'log_volatility_3',
'DJ_return_4', 'log_volume_4', 'log_volatility_4',
'DJ_return_5', 'log_volume_5', 'log_volatility_5'],
dtype='object')We frst ft a simple linear model and compute the R2 on the test data using the score() method.
In [96]: M = LinearRegression()
M.fit(X[train], Y[train])
M.score(X[∼train], Y[∼train])Out[96]: 0.4129
We reft this model, including the factor variable day_of_week. For a categorical series in pandas, we can form the indicators using the get_dummies() method.
In [97]: X_day = pd.merge(X,
pd.get_dummies(NYSE['day_of_week']),
on='date')Note that we do not have to reinstantiate the linear regression model as its fit() method accepts a design matrix and a response directly.
In [98]: M.fit(X_day[train], Y[train])
M.score(X_day[∼train], Y[∼train])Out[98]: 0.4595
This model achieves an R2 of about 46%.
To ft the RNN, we must reshape the data, as it will expect 5 lagged versions of each feature as indicated by the input_shape argument to the layer nn.RNN() below. We frst ensure the columns of our data frame are such that a reshaped matrix will have the variables correctly lagged. We use the reindex() method to do this.
462 10. Deep Learning
For an input shape (5,3), each row represents a lagged version of the three variables. The nn.RNN() layer also expects the frst row of each observation to be earliest in time, so we must reverse the current order. Hence we loop over range(5,0,-1) below, which is an example of using a slice() to index iterable objects. The general notation is start:end:step.
In [99]: ordered_cols = []for lag in range(5,0,-1):
for col in cols:
ordered_cols.append('{0}_{1}'.format(col, lag))
X = X.reindex(columns=ordered_cols)
X.columnsOut[99]: Index(['DJ_return_5', 'log_volume_5', 'log_volatility_5',
'DJ_return_4', 'log_volume_4', 'log_volatility_4',
'DJ_return_3', 'log_volume_3', 'log_volatility_3',
'DJ_return_2', 'log_volume_2', 'log_volatility_2',
'DJ_return_1', 'log_volume_1', 'log_volatility_1'],
dtype='object')We now reshape the data.
In [100]: X_rnn = X.to_numpy().reshape((-1,5,3))
X_rnn.shapeOut[100]: (6046, 5, 3)
By specifying the frst size as -1, numpy.reshape() deduces its size based on the remaining arguments.
Now we are ready to proceed with the RNN, which uses 12 hidden units, and 10% dropout. After passing through the RNN, we extract the fnal time point as val[:,-1] in forward() below. This gets passed through a 10% dropout and then fattened through a linear layer.
In [101]: class NYSEModel(nn.Module):
def __init__(self):
super(NYSEModel, self).__init__()
self.rnn = nn.RNN(3,
12,
batch_first=True)
self.dense = nn.Linear(12, 1)
self.dropout = nn.Dropout(0.1)
def forward(self, x):
val, h_n = self.rnn(x)
val = self.dense(self.dropout(val[:,-1]))
return torch.flatten(val)
nyse_model = NYSEModel()We ft the model in a similar fashion to previous networks. We supply the fit function with test data as validation data, so that when we monitor its progress and plot the history function we can see the progress on the test data. Of course we should not use this as a basis for early stopping, since then the test performance would be biased.
We form the training dataset similar to our Hitters example.
In [102]: datasets = []
for mask in [train, ∼train]:
X_rnn_t = torch.tensor(X_rnn[mask].astype(np.float32))
Y_t = torch.tensor(Y[mask].astype(np.float32))
datasets.append(TensorDataset(X_rnn_t, Y_t))
nyse_train, nyse_test = datasetsFollowing our usual pattern, we inspect the summary.
In [103]: summary(nyse_model,
input_data=X_rnn_t,
col_names=['input_size',
'output_size',
'num_params'])Out[103]: ====================================================================
Layer (type:depth-idx) Input Shape Output Shape Param #
====================================================================
NYSEModel [1770, 5, 3] [1770] --
RNN: 1-1 [1770, 5, 3] [1770, 5, 12] 204
Dropout: 1-2 [1770, 12] [1770, 12] --
Linear: 1-3 [1770, 12] [1770, 1] 13
====================================================================
Total params: 217
Trainable params: 217We again put the two datasets into a data module, with a batch size of 64.
In [104]: nyse_dm = SimpleDataModule(nyse_train,
nyse_test,
num_workers=min(4, max_num_workers),
validation=nyse_test,
batch_size=64)We run some data through our model to be sure the sizes match up correctly.
In [105]: for idx, (x, y) in enumerate(nyse_dm.train_dataloader()):
out = nyse_model(x)
print(y.size(), out.size())
if idx >= 2:
breaktorch.Size([64]) torch.Size([64])
torch.Size([64]) torch.Size([64])
torch.Size([64]) torch.Size([64])We follow our previous example for setting up a trainer for a regression problem, requesting the R2 metric to be be computed at each epoch.
In [106]: nyse_optimizer = RMSprop(nyse_model.parameters(),
lr=0.001)
nyse_module = SimpleModule.regression(nyse_model,
optimizer=nyse_optimizer,
metrics={'r2':R2Score()})Fitting the model should by now be familiar. The results on the test data are very similar to the linear AR model.
464 10. Deep Learning
In [107]: nyse_trainer = Trainer(deterministic=True,
max_epochs=200,
callbacks=[ErrorTracker()])
nyse_trainer.fit(nyse_module,
datamodule=nyse_dm)
nyse_trainer.test(nyse_module,
datamodule=nyse_dm)Out[107]: [{‘test_loss’: 0.6141, ‘test_r2’: 0.4172}]
We could also ft a model without the nn.RNN() layer by just using a nn.Flatten() layer instead. This would be a nonlinear AR model. If in addition we excluded the hidden layer, this would be equivalent to our earlier linear AR model.
Instead we will ft a nonlinear AR model using the feature set X_day that includes the day_of_week indicators. To do so, we must frst create our test and training datasets and a corresponding data module. This may seem a little burdensome, but is part of the general pipeline for torch.
In [108]: datasets = []for mask in [train, ∼train]:
X_day_t = torch.tensor(
np.asarray(X_day[mask]).astype(np.float32))
Y_t = torch.tensor(np.asarray(Y[mask]).astype(np.float32))
datasets.append(TensorDataset(X_day_t, Y_t))
day_train, day_test = datasetsCreating a data module follows a familiar pattern.
In [109]: day_dm = SimpleDataModule(day_train,
day_test,
num_workers=min(4, max_num_workers),
validation=day_test,
batch_size=64)We build a NonLinearARModel() that takes as input the 20 features and a hidden layer with 32 units. The remaining steps are familiar.
In [110]: class NonLinearARModel(nn.Module):
def __init__(self):
super(NonLinearARModel , self).__init__()
self._forward = nn.Sequential(nn.Flatten(),
nn.Linear(20, 32),
nn.ReLU(),
nn.Dropout(0.5),
nn.Linear(32, 1))
def forward(self, x):
return torch.flatten(self._forward(x))In [111]: nl_model = NonLinearARModel()nl_optimizer = RMSprop(nl_model.parameters(),
lr=0.001)
nl_module = SimpleModule.regression(nl_model,
optimizer=nl_optimizer,
metrics={'r2':R2Score()})We continue with the usual training steps, ft the model, and evaluate the test error. We see the test R2 is a slight improvement over the linear AR model that also includes day_of_week.
In [112]: nl_trainer = Trainer(deterministic=True,max_epochs=20,
callbacks=[ErrorTracker()])
nl_trainer.fit(nl_module, datamodule=day_dm)
nl_trainer.test(nl_module, datamodule=day_dm)Out[112]: [{'test_loss': 0.5625, 'test_r2': 0.4662}]10.10 Exercises
Conceptual
- Consider a neural network with two hidden layers: p = 4 input units, 2 units in the frst hidden layer, 3 units in the second hidden layer, and a single output.
This shows that the softmax function is over-parametrized. However, overregularization and SGD typically constrain the solutions so that this parametrized is not a problem.
- Consider a CNN that takes in 32 × 32 grayscale images and has a single convolution layer with three 5 × 5 convolution flters (without boundary padding).
- Draw a sketch of the input and frst hidden layer similar to Figure 10.8.
- How many parameters are in this model?
- Explain how this model can be thought of as an ordinary feedforward neural network with the individual pixels as inputs, and with constraints on the weights in the hidden units. What are the constraints?
- If there were no constraints, then how many weights would there be in the ordinary feed-forward neural network in (c)?
Applied
- Consider the simple function R(β) = sin(β) + β/10.
- Draw a graph of this function over the range β ∈ [−6, 6].
- What is the derivative of this function?
- Given β0 = 2.3, run gradient descent to fnd a local minimum of R(β) using a learning rate of ρ = 0.1. Show each of β0, β1,… in your plot, as well as the fnal answer.
- Repeat with β0 = 1.4.
- From your collection of personal photographs, pick 10 images of animals (such as dogs, cats, birds, farm animals, etc.). If the subject does not occupy a reasonable part of the image, then crop the image. Now use a pretrained image classifcation CNN as in Lab 10.9.4 to predict the class of each of your images, and report the probabilities for the top fve predicted classes for each image.
- Fit a lag-5 autoregressive model to the NYSE data, as described in the text and Lab 10.9.6. Reft the model with a 12-level factor representing the month. Does this factor improve the performance of the model?
- In Section 10.9.6, we showed how to ft a linear AR model to the NYSE data using the LinearRegression() function. However, we also mentioned that we can “fatten” the short sequences produced for the RNN model in order to ft a linear AR model. Use this latter approach to ft a linear AR model to the NYSE data. Compare the test R2 of this linear AR model to that of the linear AR model that we ft in the lab. What are the advantages/disadvantages of each approach?
- Repeat the previous exercise, but now ft a nonlinear AR model by “fattening” the short sequences produced for the RNN model.
- Consider the RNN ft to the NYSE data in Section 10.9.6. Modify the code to allow inclusion of the variable day_of_week, and ft the RNN. Compute the test R2.
- Repeat the analysis of Lab 10.9.5 on the IMDb data using a similarly structured neural network. We used 16 hidden units at each of two hidden layers. Explore the efect of increasing this to 32 and 64 units per layer, with and without 30% dropout regularization.
11 Survival Analysis and Censored Data
In this chapter, we will consider the topics of survival analysis and censored survival analysis data. These arise in the analysis of a unique kind of outcome variable: the time until an event occurs.
censored data
For example, suppose that we have conducted a fve-year medical study, in which patients have been treated for cancer. We would like to ft a model to predict patient survival time, using features such as baseline health measurements or type of treatment. At frst pass, this may sound like a regression problem of the kind discussed in Chapter 3. But there is an important complication: hopefully some or many of the patients have survived until the end of the study. Such a patient’s survival time is said to be censored: we know that it is at least fve years, but we do not know its true value. We do not want to discard this subset of surviving patients, as the fact that they survived at least fve years amounts to valuable information. However, it is not clear how to make use of this information using the techniques covered thus far in this textbook.
Though the phrase “survival analysis” evokes a medical study, the applications of survival analysis extend far beyond medicine. For example, consider a company that wishes to model churn, the process by which customers cancel subscription to a service. The company might collect data on customers over some time period, in order to model each customer’s time to cancellation as a function of demographics or other predictors. However, presumably not all customers will have canceled their subscription by the end of this time period; for such customers, the time to cancellation is censored.
In fact, survival analysis is relevant even in application areas that are unrelated to time. For instance, suppose we wish to model a person’s weight as a function of some covariates, using a dataset with measurements for a large number of people. Unfortunately, the scale used to weigh those people is unable to report weights above a certain number. Then, any weights that
© Springer Nature Switzerland AG 2023
exceed that number are censored. The survival analysis methods presented in this chapter could be used to analyze this dataset.
Survival analysis is a very well-studied topic within statistics, due to its critical importance in a variety of applications, both in and out of medicine. However, it has received relatively little attention in the machine learning community.
11.1 Survival and Censoring Times
For each individual, we suppose that there is a true survival time, T, as well survival time as a true censoring time, C. (The survival time is also known as the failure censoring time time or the event time.) The survival time represents the time at which the event of interest occurs: for instance, the time at which the patient dies, or the customer cancels his or her subscription. By contrast, the censoring time is the time at which censoring occurs: for example, the time at which the patient drops out of the study or the study ends.
failure time event time
We observe either the survival time T or else the censoring time C. Specifcally, we observe the random variable
\[Y = \min(T, C). \tag{11.1}\]
In other words, if the event occurs before censoring (i.e. T <C) then we observe the true survival time T; however, if censoring occurs before the event (T >C) then we observe the censoring time. We also observe a status indicator,
\[ \delta = \begin{cases} 1 & \text{if } T \le C \\ 0 & \text{if } T > C. \end{cases} \]
Thus, δ = 1 if we observe the true survival time, and δ = 0 if we instead observe the censoring time.
Now, suppose we observe n (Y, δ) pairs, which we denote as (y1, δ1),…, (yn, δn). Figure 11.1 displays an example from a (fctitious) medical study in which we observe n = 4 patients for a 365-day follow-up period. For patients 1 and 3, we observe the time to event (such as death or disease relapse) T = ti. Patient 2 was alive when the study ended, and patient 4 dropped out of the study, or was “lost to follow-up”; for these patients we observe C = ci. Therefore, y1 = t1, y3 = t3, y2 = c2, y4 = c4, δ1 = δ3 = 1, and δ2 = δ4 = 0.
11.2 A Closer Look at Censoring
In order to analyze survival data, we need to make some assumptions about why censoring has occurred. For instance, suppose that a number of patients drop out of a cancer study early because they are very sick. An analysis that does not take into consideration the reason why the patients dropped out will likely overestimate the true average survival time. Similarly, suppose that males who are very sick are more likely to drop out of the study than
FIGURE 11.1. Illustration of censored survival data. For patients 1 and 3, the event was observed. Patient 2 was alive when the study ended. Patient 4 dropped out of the study.
females who are very sick. Then a comparison of male and female survival times may wrongly suggest that males survive longer than females.
In general, we need to assume that the censoring mechanism is independent: conditional on the features, the event time T is independent of the censoring time C. The two examples above violate the assumption of independent censoring. Typically, it is not possible to determine from the data itself whether the censoring mechanism is independent. Instead, one has to carefully consider the data collection process in order to determine whether independent censoring is a reasonable assumption. In the remainder of this chapter, we will assume that the censoring mechanism is independent.1
In this chapter, we focus on right censoring, which occurs when T ≥ Y , i.e. the true event time T is at least as large as the observed time Y . (Notice that T ≥ Y is a consequence of (11.1). Right censoring derives its name from the fact that time is typically displayed from left to right, as in Figure 11.1.) However, other types of censoring are possible. For instance, in left censoring, the true event time T is less than or equal to the observed time Y . For example, in a study of pregnancy duration, suppose that we survey patients 250 days after conception, when some have already had their babies. Then we know that for those patients, pregnancy duration is less than 250 days. More generally, interval censoring refers to the setting in which we do not know the exact event time, but we know that it falls in some interval. For instance, this setting arises if we survey patients once per week in order to determine whether the event has occurred. While left censoring and interval censoring can be accommodated using variants of the ideas presented in this chapter, in what follows we focus specifcally on right censoring.
1The assumption of independent censoring can be relaxed somewhat using the notion of non-informative censoring; however, the defnition of non-informative censoring is too technical for this book.
11.3 The Kaplan–Meier Survival Curve
The survival curve, or survival function, is defned as survival
\[S(t) = \Pr(T > t). \tag{11.2}\]
curve
function
This decreasing function quantifes the probability of surviving past time t. For example, suppose that a company is interested in modeling customer churn. Let T represent the time that a customer cancels a subscription to the company’s service. Then S(t) represents the probability that a customer cancels later than time t. The larger the value of S(t), the less likely that the customer will cancel before time t.
In this section, we will consider the task of estimating the survival curve. Our investigation is motivated by the BrainCancer dataset, which contains the survival times for patients with primary brain tumors undergoing treatment with stereotactic radiation methods.2 The predictors are gtv (gross tumor volume, in cubic centimeters); sex (male or female); diagnosis (meningioma, LG glioma, HG glioma, or other); loc (the tumor location: either infratentorial or supratentorial); ki (Karnofsky index); and stereo (stereotactic method: either stereotactic radiosurgery or fractionated stereotactic radiotherapy, abbreviated as SRS and SRT, respectively). Only 53 of the 88 patients were still alive at the end of the study.
Now, we consider the task of estimating the survival curve (11.2) for these data. To estimate S(20) = Pr(T > 20), the probability that a patient survives for at least t = 20 months, it is tempting to simply compute the proportion of patients who are known to have survived past 20 months, i.e. the proportion of patients for whom Y > 20. This turns out to be 48/88, or approximately 55%. However, this does not seem quite right, since Y and T represent diferent quantities. In particular, 17 of the 40 patients who did not survive to 20 months were actually censored, and this analysis implicitly assumes that T < 20 for all of those censored patients; of course, we do not know whether that is true.
Alternatively, to estimate S(20), we could consider computing the proportion of patients for whom Y > 20, out of the 71 patients who were not censored by time t = 20; this comes out to 48/71, or approximately 68%. However, this is not quite right either, since it amounts to completely ignoring the patients who were censored before time t = 20, even though the time at which they are censored is potentially informative. For instance, a patient who was censored at time t = 19.9 likely would have survived past t = 20 had he or she not been censored.
We have seen that estimating S(t) is complicated by the presence of censoring. We now present an approach to overcome these challenges. We let d1 < d2 < ··· < dK denote the K unique death times among the noncensored patients, and we let qk denote the number of patients who died at time dk. For k = 1,…,K, we let rk denote the number of patients alive
2This dataset is described in the following paper: Selingerová et al. (2016) Survival of patients with primary brain tumors: Comparison of two statistical approaches. PLoS One, 11(2):e0148733.
and in the study just before dk; these are the at risk patients. The set of patients that are at risk at a given time are referred to as the risk set. risk set By the law of total probability,3
\[\begin{aligned} \Pr(T > d\_k) &= \Pr(T > d\_k | T > d\_{k-1}) \Pr(T > d\_{k-1}) \\ &+ \Pr(T > d\_k | T \le d\_{k-1}) \Pr(T \le d\_{k-1}). \end{aligned}\]
The fact that dk−1 < dk implies that Pr(T >dk|T ≤ dk−1)=0 (it is impossible for a patient to survive past time dk if he or she did not survive until an earlier time dk−1). Therefore,
\[S(d\_k) = \Pr(T > d\_k) = \Pr(T > d\_k | T > d\_{k-1}) \Pr(T > d\_{k-1}).\]
Plugging in (11.2) again, we see that
\[S(d\_k) = \Pr(T > d\_k | T > d\_{k-1}) S(d\_{k-1}).\]
This implies that
\[S(d\_k) = \Pr(T > d\_k | T > d\_{k-1}) \times \dots \times \Pr(T > d\_2 | T > d\_1) \Pr(T > d\_1).\]
We now must simply plug in estimates of each of the terms on the righthand side of the previous equation. It is natural to use the estimator
\[\Pr(T > d\_j | T > d\_{j-1}) = (r\_j - q\_j) / r\_j,\]
which is the fraction of the risk set at time dj who survived past time dj . This leads to the Kaplan–Meier estimator of the survival curve: Kaplan–
Meier estimator
\[\widehat{S}(d\_k) = \prod\_{j=1}^{k} \left( \frac{r\_j - q\_j}{r\_j} \right). \tag{11.3}\]
For times t between dk and dk+1, we set SI(t) = SI(dk). Consequently, the Kaplan–Meier survival curve has a step-like shape.
The Kaplan–Meier survival curve for the BrainCancer data is displayed in Figure 11.2. Each point in the solid step-like curve shows the estimated probability of surviving past the time indicated on the horizontal axis. The estimated probability of survival past 20 months is 71%, which is quite a bit higher than the naive estimates of 55% and 68% presented earlier.
The sequential construction of the Kaplan–Meier estimator — starting at time zero and mapping out the observed events as they unfold in time is fundamental to many of the key techniques in survival analysis. These include the log-rank test of Section 11.4, and Cox’s proportional hazard model of Section 11.5.2.
3The law of total probability states that for any two events A and B, Pr(A) = Pr(A|B) Pr(B) + Pr(A|Bc) Pr(Bc), where Bc is the complement of the event B, i.e. it is the event that B does not hold.
FIGURE 11.2. For the BrainCancer data, we display the Kaplan–Meier survival curve (solid curve), along with standard error bands (dashed curves).
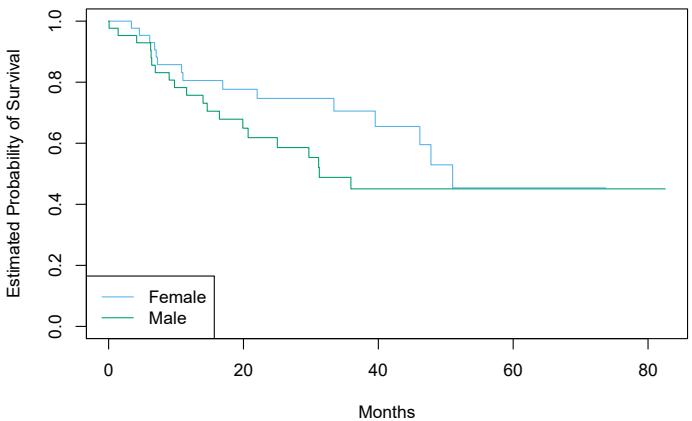
FIGURE 11.3. For the BrainCancer data, Kaplan–Meier survival curves for males and females are displayed.
11.4 The Log-Rank Test
We now continue our analysis of the BrainCancer data introduced in Section 11.3. We wish to compare the survival of males to that of females. Figure 11.3 shows the Kaplan–Meier survival curves for the two groups. Females seem to fare a little better up to about 50 months, but then the two curves both level of to about 50%. How can we carry out a formal test of equality of the two survival curves?
At frst glance, a two-sample t-test seems like an obvious choice: we could test whether the mean survival time among the females equals the mean survival time among the males. But the presence of censoring again creates a complication. To overcome this challenge, we will conduct a log-rank test, 4
log-rank test
| Group 1 | Group 2 | Total | |
|---|---|---|---|
| Died | q1k | q2k | qk |
| Survived | r1k − q1k |
r2k − q2k |
rk − qk |
| Total | r1k | r2k | rk |
TABLE 11.1. Among the set of patients at risk at time dk, the number of patients who died and survived in each of two groups is reported.
which examines how the events in each group unfold sequentially in time.
Recall from Section 11.3 that d1 < d2 < ··· < dK are the unique death times among the non-censored patients, rk is the number of patients at risk at time dk, and qk is the number of patients who died at time dk. We further defne r1k and r2k to be the number of patients in groups 1 and 2, respectively, who are at risk at time dk. Similarly, we defne q1k and q2k to be the number of patients in groups 1 and 2, respectively, who died at time dk. Note that r1k + r2k = rk and q1k + q2k = qk.
At each death time dk, we construct a 2 × 2 table of counts of the form shown in Table 11.1. Note that if the death times are unique (i.e. no two individuals die at the same time), then one of q1k and q2k equals one, and the other equals zero.
The main idea behind the log-rank test statistic is as follows. In order to test H0 : E(X) = µ for some random variable X, one approach is to construct a test statistic of the form
\[W = \frac{X - \mu}{\sqrt{\text{Var}(X)}}.\tag{11.4}\]
To construct the log-rank test statistic, we compute a quantity that takes exactly the form (11.4), with X = #K k=1 q1k, where q1k is given in the top left of Table 11.1.
In greater detail, if there is no diference in survival between the two groups, and conditioning on the row and column totals in Table 11.1, the expected value of q1k is
\[ \mu\_k = \frac{r\_{1k}}{r\_k} q\_k.\tag{11.5} \]
So the expected value of X = #K k=1 q1k is µ = #K k=1 r1k rk qk. Furthermore, it can be shown5 that the variance of q1k is
\[\text{Var}\left(q\_{1k}\right) = \frac{q\_k(r\_{1k}/r\_k)(1 - r\_{1k}/r\_k)(r\_k - q\_k)}{r\_k - 1}.\tag{11.6}\]
Though q11,…,q1K may be correlated, we nonetheless estimate
\[\operatorname{Var}\left(\sum\_{k=1}^{K} q\_{1k}\right) \approx \sum\_{k=1}^{K} \operatorname{Var}\left(q\_{1k}\right) = \sum\_{k=1}^{K} \frac{q\_k(r\_{1k}/r\_k)(1 - r\_{1k}/r\_k)(r\_k - q\_k)}{r\_k - 1}.\tag{11.7}\]
4The log-rank test is also known as the Mantel–Haenszel test or Cochran–Mantel– Haenszel test.
5For details, see Exercise 7 at the end of this chapter.
Therefore, to compute the log-rank test statistic, we simply proceed as in (11.4), with X = #K k=1 q1k, making use of (11.5) and (11.7). That is, we calculate
\[W = \frac{\sum\_{k=1}^{K} \left(q\_{1k} - \mu\_k\right)}{\sqrt{\sum\_{k=1}^{K} \text{Var}\left(q\_{1k}\right)}} = \frac{\sum\_{k=1}^{K} \left(q\_{1k} - \frac{q\_k}{r\_k}r\_{1k}\right)}{\sqrt{\sum\_{k=1}^{K} \frac{q\_k(r\_{1k}/r\_k)(1 - r\_{1k}/r\_k)(r\_k - q\_k)}{r\_k - 1}}}. \tag{11.8}\]
When the sample size is large, the log-rank test statistic W has approximately a standard normal distribution; this can be used to compute a p-value for the null hypothesis that there is no diference between the survival curves in the two groups.6
Comparing the survival times of females and males on the BrainCancer data gives a log-rank test statistic of W = 1.2, which corresponds to a twosided p-value of 0.2 using the theoretical null distribution, and a p-value of 0.25 using the permutation null distribution with 1,000 permutations. Thus, we cannot reject the null hypothesis of no diference in survival curves between females and males.
The log-rank test is closely related to Cox’s proportional hazards model, which we discuss in Section 11.5.2.
11.5 Regression Models With a Survival Response
We now consider the task of ftting a regression model to survival data. As in Section 11.1, the observations are of the form (Y, δ), where Y = min(T,C) is the (possibly censored) survival time, and δ is an indicator variable that equals 1 if T ≤ C. Furthermore, X ∈ Rp is a vector of p features. We wish to predict the true survival time T.
Since the observed quantity Y is positive and may have a long right tail, we might be tempted to ft a linear regression of log(Y ) on X. But as the reader will surely guess, censoring again creates a problem since we are actually interested in predicting T and not Y . To overcome this difculty, we instead make use of a sequential construction, similar to the constructions of the Kaplan–Meier survival curve in Section 11.3 and the log-rank test in Section 11.4.
11.5.1 The Hazard Function
The hazard function or hazard rate — also known as the force of mortality hazard — is formally defned as function
\[h(t) = \lim\_{\Delta t \to 0} \frac{\Pr(t < T \le t + \Delta t | T > t)}{\Delta t},\tag{11.9}\]
6Alternatively, we can estimate the p-value via permutations, using ideas that will be presented in Section 13.5. The permutation distribution is obtained by randomly swapping the labels for the observations in the two groups.
where T is the (unobserved) survival time. It is the death rate in the instant after time t, given survival past that time.7 In (11.9), we take the limit as ∆t approaches zero, so we can think of ∆t as being an extremely tiny number. Thus, more informally, (11.9) implies that
\[h(t) \approx \frac{\Pr(t < T \le t + \Delta t | T > t)}{\Delta t}\]
for some arbitrarily small ∆t.
Why should we care about the hazard function? First of all, it is closely related to the survival curve (11.2), as we will see next. Second, it turns out that a key approach for modeling survival data as a function of covariates relies heavily on the hazard function; we will introduce this approach — Cox’s proportional hazards model — in Section 11.5.2.
We now consider the hazard function h(t) in a bit more detail. Recall that for two events A and B, the probability of A given B can be expressed as Pr(A | B) = Pr(A ∩ B)/Pr(B), i.e. the probability that A and B both occur divided by the probability that B occurs. Furthermore, recall from (11.2) that S(t) = Pr(T >t). Thus,
\[\begin{split} h(t) &= \lim\_{\Delta t \to 0} \frac{\Pr\left( (t < T \le t + \Delta t) \cap (T > t) \right) / \Delta t}{\Pr(T > t)} \\ &= \lim\_{\Delta t \to 0} \frac{\Pr(t < T \le t + \Delta t) / \Delta t}{\Pr(T > t)} \\ &= \frac{f(t)}{S(t)}, \end{split} \tag{11.10}\]
where
\[f(t) = \lim\_{\Delta t \to 0} \frac{\Pr(t < T \le t + \Delta t)}{\Delta t} \tag{11.11}\]
is the probability density function associated with T, i.e. it is the instanta- probability neous rate of death at time t. The second equality in (11.10) made use of the fact that if t<T ≤ t + ∆t, then it must be the case that T >t.
density function
Equation 11.10 implies a relationship between the hazard function h(t), the survival function S(t), and the probability density function f(t). In fact, these are three equivalent ways8 of describing the distribution of T.
The likelihood associated with the ith observation is
\[L\_i = \begin{cases} f(y\_i) & \text{if the } i \text{th observation is not censored} \\ S(y\_i) & \text{if the } i \text{th observation is censored} \\ \end{cases}\]
\[= f(y\_i)^{\delta\_i} S(y\_i)^{1-\delta\_i}. \tag{11.12}\]
The intuition behind (11.12) is as follows: if Y = yi and the ith observation is not censored, then the likelihood is the probability of dying in a tiny interval around time yi. If the ith observation is censored, then the likelihood
7Due to the ∆t in the denominator of (11.9), the hazard function is a rate of death, rather than a probability of death. However, higher values of h(t) directly correspond to a higher probability of death, just as higher values of a probability density function correspond to more likely outcomes for a random variable. In fact, h(t) is the probability density function for T conditional on T >t.
8See Exercise 8.
is the probability of surviving at least until time yi. Assuming that the n observations are independent, the likelihood for the data takes the form
\[L = \prod\_{i=1}^{n} f(y\_i)^{\delta\_i} S(y\_i)^{1-\delta\_i} = \prod\_{i=1}^{n} h(y\_i)^{\delta\_i} S(y\_i),\tag{11.13}\]
where the second equality follows from (11.10).
We now consider the task of modeling the survival times. If we assume exponential survival, i.e. that the probability density function of the survival time T takes the form f(t) = λ exp(−λt), then estimating the parameter λ by maximizing the likelihood in (11.13) is straightforward.9 Alternatively, we could assume that the survival times are drawn from a more fexible family of distributions, such as the Gamma or Weibull family. Another possibility is to model the survival times non-parametrically, as was done in Section 11.3 using the Kaplan–Meier estimator.
However, what we would really like to do is model the survival time as a function of the covariates. To do this, it is convenient to work directly with the hazard function, instead of the probability density function.10 One possible approach is to assume a functional form for the hazard function h(t|xi), such as h(t|xi) = exp E β0 + #p j=1 βjxijF , where the exponent function guarantees that the hazard function is non-negative. Note that the exponential hazard function is special, in that it does not vary with time.11 Given h(t|xi), we could calculate S(t|xi). Plugging these equations into (11.13), we could then maximize the likelihood in order to estimate the parameter β = (β0, β1,…, βp)T . However, this approach is quite restrictive, in the sense that it requires us to make a very stringent assumption on the form of the hazard function h(t|xi). In the next section, we will consider a much more fexible approach.
11.5.2 Proportional Hazards
The Proportional Hazards Assumption
The proportional hazards assumption states that proportional
\[h(t|x\_i) = h\_0(t) \exp\left(\sum\_{j=1}^p x\_{ij}\beta\_j\right),\tag{11.14}\]
where h0(t) ≥ 0 is an unspecifed function, known as the baseline hazard. baseline hazard It is the hazard function for an individual with features xi1 = ··· = xip = 0. The name “proportional hazards” arises from the fact that the hazard function for an individual with feature vector xi is some unknown function
9See Exercise 9.
10Given the close relationship between the hazard function h(t) and the density function f(t) explored in Exercise 8, posing an assumption about the form of the hazard function is closely related to posing an assumption about the form of the density function, as was done in the previous paragraph.
11The notation h(t|xi) indicates that we are now considering the hazard function for the ith observation conditional on the values of the covariates, xi.
FIGURE 11.4. Top: In a simple example with p = 1 and a binary covariate xi ∈ {0, 1}, the log hazard and the survival function under the model (11.14) are shown (green for xi = 0 and black for xi = 1). Because of the proportional hazards assumption (11.14), the log hazard functions difer by a constant, and the survival functions do not cross. Bottom: Again we have a single binary covariate xi ∈ {0, 1}. However, the proportional hazards assumption (11.14) does not hold. The log hazard functions cross, as do the survival functions.
h0(t) times the factor exp E#p j=1 xijβj F . The quantity exp E#p j=1 xijβj F is called the relative risk for the feature vector xi = (xi1,…,xip)T , relative to that for the feature vector xi = (0,…, 0)T .
What does it mean that the baseline hazard function h0(t) in (11.14) is unspecifed? Basically, we make no assumptions about its functional form. We allow the instantaneous probability of death at time t, given that one has survived at least until time t, to take any form. This means that the hazard function is very fexible and can model a wide range of relationships between the covariates and survival time. Our only assumption is that a one-unit increase in xij corresponds to an increase in h(t|xi) by a factor of exp(βj ).
An illustration of the proportional hazards assumption (11.14) is given in Figure 11.4, in a simple setting with a single binary covariate xi ∈ {0, 1} (so that p = 1). In the top row, the proportional hazards assumption (11.14) holds. Thus, the hazard functions of the two groups are a constant multiple of each other, so that on the log scale, the gap between them is constant. Furthermore, the survival curves never cross, and in fact the gap between the survival curves tends to (initially) increase over time. By contrast, in the bottom row, (11.14) does not hold. We see that the log hazard functions for the two groups cross, as do the survival curves.
480 11. Survival Analysis and Censored Data
Cox’s Proportional Hazards Model
Because the form of h0(t) in the proportional hazards assumption (11.14) is unknown, we cannot simply plug h(t|xi) into the likelihood (11.13) and then estimate β = (β1,…, βp)T by maximum likelihood. The magic of Cox’s proportional hazards model lies in the fact that it is in fact possible Cox’s to estimate β without having to specify the form of h0(t).
proportional hazards model
To accomplish this, we make use of the same “sequential in time” logic that we used to derive the Kaplan–Meier survival curve and the log-rank test. For simplicity, assume that there are no ties among the failure, or death, times: i.e. each failure occurs at a distinct time. Assume that δi = 1, i.e. the ith observation is uncensored, and thus yi is its failure time. Then the hazard function for the ith observation at time yi is h(yi|xi) = h0(yi) exp E#p j=1 xijβj F , and the total hazard at time yi for the at risk observations12 is
\[\sum\_{i': y\_{i'} \ge y\_i} h\_0(y\_i) \exp\left(\sum\_{j=1}^p x\_{i'j} \beta\_j\right).\]
Therefore, the probability that the ith observation is the one to fail at time yi (as opposed to one of the other observations in the risk set) is
\[\frac{h\_0(y\_i)\exp\left(\sum\_{j=1}^p x\_{ij}\beta\_j\right)}{\sum\_{i':y\_{i'}\ge y\_i} h\_0(y\_i)\exp\left(\sum\_{j=1}^p x\_{i'j}\beta\_j\right)} = \frac{\exp\left(\sum\_{j=1}^p x\_{ij}\beta\_j\right)}{\sum\_{i':y\_{i'}\ge y\_i} \exp\left(\sum\_{j=1}^p x\_{i'j}\beta\_j\right)}.\tag{11.15}\]
Notice that the unspecifed baseline hazard function h0(yi) cancels out of the numerator and denominator!
The partial likelihood is simply the product of these probabilities over all partial likelihood of the uncensored observations,
\[PL(\beta) = \prod\_{i:\delta\_i=1} \frac{\exp\left(\sum\_{j=1}^p x\_{ij}\beta\_j\right)}{\sum\_{i':y\_{i'}\ge y\_i} \exp\left(\sum\_{j=1}^p x\_{i'j}\beta\_j\right)}.\tag{11.16}\]
Critically, the partial likelihood is valid regardless of the true value of h0(t), making the model very fexible and robust.13
To estimate β, we simply maximize the partial likelihood (11.16) with respect to β. As was the case for logistic regression in Chapter 4, no closedform solution is available, and so iterative algorithms are required.
In addition to estimating β, we can also obtain other model outputs that we saw in the context of least squares regression in Chapter 3 and logistic regression in Chapter 4. For example, we can obtain p-values corresponding
12Recall that the “at risk” observations at time yi are those that are still at risk of failure, i.e. those that have not yet failed or been censored before time yi. 13In general, the partial likelihood is used in settings where it is difcult to compute
the full likelihood for all of the parameters. Instead, we compute a likelihood for just the parameters of primary interest: in this case, β1,…, βp. It can be shown that maximizing (11.16) provides good estimates for these parameters.
to particular null hypotheses (e.g. H0 : βj = 0), as well as confdence intervals associated with the coefcients.
Connection With The Log-Rank Test
Suppose we have just a single predictor (p = 1), which we assume to be binary, i.e. xi ∈ {0, 1}. In order to determine whether there is a diference between the survival times of the observations in the group {i : xi = 0} and those in the group {i : xi = 1}, we can consider taking two possible approaches:
Approach #1: Fit a Cox proportional hazards model, and test the null hypothesis H0 : β = 0. (Since p = 1, β is a scalar.)
Approach #2: Perform a log-rank test to compare the two groups, as in Section 11.4.
Which one should we prefer?
In fact, there is a close relationship between these two approaches. In particular, when taking Approach #1, there are a number of possible ways to test H0. One way is known as a score test. It turns out that in the case of a single binary covariate, the score test for H0 : β = 0 in Cox’s proportional hazards model is exactly equal to the log-rank test. In other words, it does not matter whether we take Approach #1 or Approach #2!
Additional Details
The discussion of Cox’s proportional hazards model glossed over a few subtleties:
- There is no intercept in (11.14) nor in the equations that follow, because an intercept can be absorbed into the baseline hazard h0(t).
- We have assumed that there are no tied failure times. In the case of ties, the exact form of the partial likelihood (11.16) is a bit more complicated, and a number of computational approximations must be used.
- (11.16) is known as the partial likelihood because it is not exactly a likelihood. That is, it does not correspond exactly to the probability of the data under the assumption (11.14). However, it is a very good approximation.
- We have focused only on estimation of the coefcients β = (β1,…, βp)T . However, at times we may also wish to estimate the baseline hazard h0(t), for instance so that we can estimate the survival curve S(t|x) for an individual with feature vector x. The details are beyond the scope of this book. Estimation of h0(t) is implemented in the lifelines package in Python, which we will see in Section 11.8.
11.5.3 Example: Brain Cancer Data
Table 11.2 shows the result of ftting the proportional hazards model to the BrainCancer data, which was originally described in Section 11.3. The coefcient column displays βˆj . The results indicate, for instance, that the estimated hazard for a male patient is e0.18 = 1.2 times greater than for a female patient: in other words, with all other features held fxed, males have a 1.2 times greater chance of dying than females, at any point in time. However, the p-value is 0.61, which indicates that this diference between males and females is not signifcant.
As another example, we also see that each one-unit increase in the Karnofsky index corresponds to a multiplier of exp(−0.05) = 0.95 in the instantaneous chance of dying. In other words, the higher the Karnofsky index, the lower the chance of dying at any given point in time. This efect is highly signifcant, with a p-value of 0.0027.
| Coefcient | Std. error | z-statistic | p-value | |
|---|---|---|---|---|
| sex[Male] | 0.18 | 0.36 | 0.51 | 0.61 |
| diagnosis[LG Glioma] | 0.92 | 0.64 | 1.43 | 0.15 |
| diagnosis[HG Glioma] | 2.15 | 0.45 | 4.78 | 0.00 |
| diagnosis[Other] | 0.89 | 0.66 | 1.35 | 0.18 |
| loc[Supratentorial] | 0.44 | 0.70 | 0.63 | 0.53 |
| ki | -0.05 | 0.02 | -3.00 | <0.01 |
| gtv | 0.03 | 0.02 | 1.54 | 0.12 |
| stereo[SRT] | 0.18 | 0.60 | 0.30 | 0.77 |
TABLE 11.2. Results for Cox’s proportional hazards model ft to the BrainCancer data, which was frst described in Section 11.3. The variable diagnosis is qualitative with four levels: meningioma, LG glioma, HG glioma, or other. The variables sex, loc, and stereo are binary.
11.5.4 Example: Publication Data
Next, we consider the dataset Publication involving the time to publication of journal papers reporting the results of clinical trials funded by the National Heart, Lung, and Blood Institute.14 For 244 trials, the time in months until publication is recorded. Of the 244 trials, only 156 were published during the study period; the remaining studies were censored. The covariates include whether the trial focused on a clinical endpoint (clinend), whether the trial involved multiple centers (multi), the funding mechanism within the National Institutes of Health (mech), trial sample size (sampsize), budget (budget), impact (impact, related to the number of citations), and whether the trial produced a positive (signifcant) result (posres). The last covariate is particularly interesting, as a number of studies have suggested that positive trials have a higher publication rate.
14This dataset is described in the following paper: Gordon et al. (2013) Publication of trials funded by the National Heart, Lung, and Blood Institute. New England Journal of Medicine, 369(20):1926–1934.
FIGURE 11.5. Survival curves for time until publication for the Publication data described in Section 11.5.4, stratifed by whether or not the study produced a positive result.
Figure 11.5 shows the Kaplan–Meier curves for the time until publication, stratifed by whether or not the study produced a positive result. We see slight evidence that time until publication is lower for studies with a positive result. However, the log-rank test yields a very unimpressive p-value of 0.36.
We now consider a more careful analysis that makes use of all of the available predictors. The results of ftting Cox’s proportional hazards model using all of the available features are shown in Table 11.3. We fnd that the chance of publication of a study with a positive result is e0.55 = 1.74 times higher than the chance of publication of a study with a negative result at any point in time, holding all other covariates fxed. The very small p-value associated with posres in Table 11.3 indicates that this result is highly signifcant. This is striking, especially in light of our earlier fnding that a log-rank test comparing time to publication for studies with positive versus negative results yielded a p-value of 0.36. How can we explain this discrepancy? The answer stems from the fact that the log-rank test did not consider any other covariates, whereas the results in Table 11.3 are based on a Cox model using all of the available covariates. In other words, after we adjust for all of the other covariates, then whether or not the study yielded a positive result is highly predictive of the time to publication.
In order to gain more insight into this result, in Figure 11.6 we display estimates of the survival curves associated with positive and negative results, adjusting for the other predictors. To produce these survival curves, we estimated the underlying baseline hazard h0(t). We also needed to select representative values for the other predictors; we used the mean value for each predictor, except for the categorical predictor mech, for which we used the most prevalent category (R01). Adjusting for the other predictors, we now see a clear diference in the survival curves between studies with positive versus negative results.
Other interesting insights can be gleaned from Table 11.3. For example, studies with a clinical endpoint are more likely to be published at any given point in time than those with a non-clinical endpoint. The funding
| Coefcient | Std. error | z-statistic | p-value | |
|---|---|---|---|---|
| posres[Yes] | 0.55 | 0.18 | 3.02 | 0.00 |
| multi[Yes] | 0.15 | 0.31 | 0.47 | 0.64 |
| clinend[Yes] | 0.51 | 0.27 | 1.89 | 0.06 |
| mech[K01] | 1.05 | 1.06 | 1.00 | 0.32 |
| mech[K23] | -0.48 | 1.05 | -0.45 | 0.65 |
| mech[P01] | -0.31 | 0.78 | -0.40 | 0.69 |
| mech[P50] | 0.60 | 1.06 | 0.57 | 0.57 |
| mech[R01] | 0.10 | 0.32 | 0.30 | 0.76 |
| mech[R18] | 1.05 | 1.05 | 0.99 | 0.32 |
| mech[R21] | -0.05 | 1.06 | -0.04 | 0.97 |
| mech[R24,K24] | 0.81 | 1.05 | 0.77 | 0.44 |
| mech[R42] | -14.78 | 3414.38 | -0.00 | 1.00 |
| mech[R44] | -0.57 | 0.77 | -0.73 | 0.46 |
| mech[RC2] | -14.92 | 2243.60 | -0.01 | 0.99 |
| mech[U01] | -0.22 | 0.32 | -0.70 | 0.48 |
| mech[U54] | 0.47 | 1.07 | 0.44 | 0.66 |
| sampsize | 0.00 | 0.00 | 0.19 | 0.85 |
| budget | 0.00 | 0.00 | 1.67 | 0.09 |
| impact | 0.06 | 0.01 | 8.23 | 0.00 |
TABLE 11.3. Results for Cox’s proportional hazards model ft to the Publication data, using all of the available features. The features posres, multi, and clinend are binary. The feature mech is qualitative with 14 levels; it is coded so that the baseline level is Contract.
mechanism did not appear to be signifcantly associated with time until publication.
11.6 Shrinkage for the Cox Model
In this section, we illustrate that the shrinkage methods of Section 6.2 can be applied to the survival data setting. In particular, motivated by the “loss+penalty” formulation of Section 6.2, we consider minimizing a penalized version of the negative log partial likelihood in (11.16),
\[-\log\left(\prod\_{i:\delta\_i=1} \frac{\exp\left(\sum\_{j=1}^p x\_{ij}\beta\_j\right)}{\sum\_{i':y\_{i'}\ge y\_i} \exp\left(\sum\_{j=1}^p x\_{i'j}\beta\_j\right)}\right) + \lambda P(\beta),\tag{11.17}\]
with respect to β = (β1,…, βp)T . We might take P(β) = #p j=1 β2 j , which corresponds to a ridge penalty, or P(β) = #p j=1 |βj |, which corresponds to a lasso penalty.
In (11.17), λ is a non-negative tuning parameter; typically we will minimize it over a range of values of λ. When λ = 0, then minimizing (11.17) is equivalent to simply maximizing the usual Cox partial likelihood (11.16). However, when λ > 0, then minimizing (11.17) yields a shrunken version of the coefcient estimates. When λ is large, then using a ridge penalty will give small coefcients that are not exactly equal to zero. By contrast, for a
FIGURE 11.6. For the Publication data, we display survival curves for time until publication, stratifed by whether or not the study produced a positive result, after adjusting for all other covariates.
sufciently large value of λ, using a lasso penalty will give some coefcients that are exactly equal to zero.
We now apply the lasso-penalized Cox model to the Publication data, described in Section 11.5.4. We frst randomly split the 244 trials into equallysized training and test sets. The cross-validation results from the training set are shown in Figure 11.7. The “partial likelihood deviance”, shown on the y-axis, is twice the cross-validated negative log partial likelihood; it plays the role of the cross-validation error.15 Note the “U-shape” of the partial likelihood deviance: just as we saw in previous chapters, the crossvalidation error is minimized for an intermediate level of model complexity. Specifcally, this occurs when just two predictors, budget and impact, have non-zero estimated coefcients.
Now, how do we apply this model to the test set? This brings up an important conceptual point: in essence, there is no simple way to compare predicted survival times and true survival times on the test set. The frst problem is that some of the observations are censored, and so the true survival times for those observations are unobserved. The second issue arises from the fact that in the Cox model, rather than predicting a single survival time given a covariate vector x, we instead estimate an entire survival curve, S(t|x), as a function of t.
Therefore, to assess the model ft, we must take a diferent approach, which involves stratifying the observations using the coefcient estimates. In particular, for each test observation, we compute the “risk” score
budgeti · βˆbudget + impacti · βˆimpact,
where βˆbudget and βˆimpact are the coefcient estimates for these two features from the training set. We then use these risk scores to categorize the observations based on their “risk”. For instance, the high risk group consists of the observations for which budgeti · βˆbudget +impacti · βˆimpact is largest; by
15Cross-validation for the Cox model is more involved than for linear or logistic regression, because the objective function is not a sum over the observations.
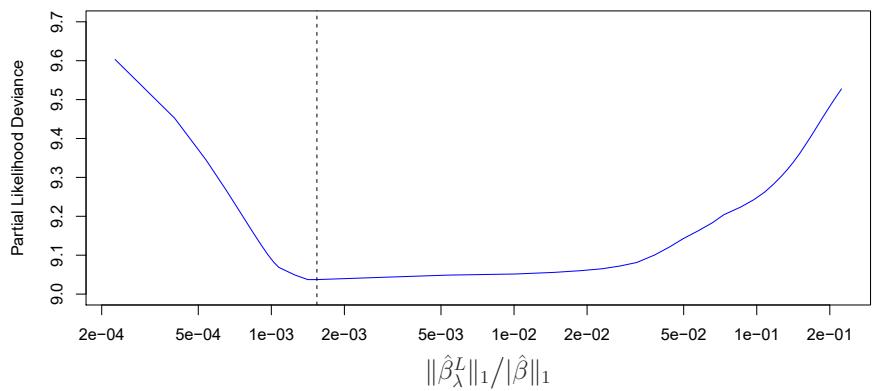
FIGURE 11.7. For the Publication data described in Section 11.5.4, cross-validation results for the lasso-penalized Cox model are shown. The y-axis displays the partial likelihood deviance, which plays the role of the cross-validation error. The x-axis displays the ℓ1 norm (that is, the sum of the absolute values) of the coefcients of the lasso-penalized Cox model with tuning parameter λ, divided by the ℓ1 norm of the coefcients of the unpenalized Cox model. The dashed line indicates the minimum cross-validation error.
(11.14), we see that these are the observations for which the instantaneous probability of being published at any moment in time is largest. In other words, the high risk group consists of the trials that are likely to be published sooner. On the Publication data, we stratify the observations into tertiles of low, medium, and high risk. The resulting survival curves for each of the three strata are displayed in Figure 11.8. We see that there is clear separation between the three strata, and that the strata are correctly ordered in terms of low, medium, and high risk of publication.
11.7 Additional Topics
11.7.1 Area Under the Curve for Survival Analysis
In Chapter 4, we introduced the area under the ROC curve — often referred to as the “AUC” — as a way to quantify the performance of a two-class classifer. Defne the score for the ith observation to be the classifer’s estimate of Pr(Y = 1|X = xi). It turns out that if we consider all pairs consisting of one observation in Class 1 and one observation in Class 2, then the AUC is the fraction of pairs for which the score for the observation in Class 1 exceeds the score for the observation in Class 2.
This suggests a way to generalize the notion of AUC to survival analysis. We calculate an estimated risk score, ηˆi = βˆ1xi1 + ··· + βˆpxip, for i = 1,…,n, using the Cox model coefcients. If ηˆi′ > ηˆi, then the model predicts that the i ′ th observation has a larger hazard than the ith observation, and thus that the survival time ti will be greater than ti′ . Thus, it is tempting to try to generalize AUC by computing the proportion of observations for which ti > ti′ and ηˆi′ > ηˆi. However, things are not quite so easy, because recall that we do not observe t1,…,tn; instead, we observe
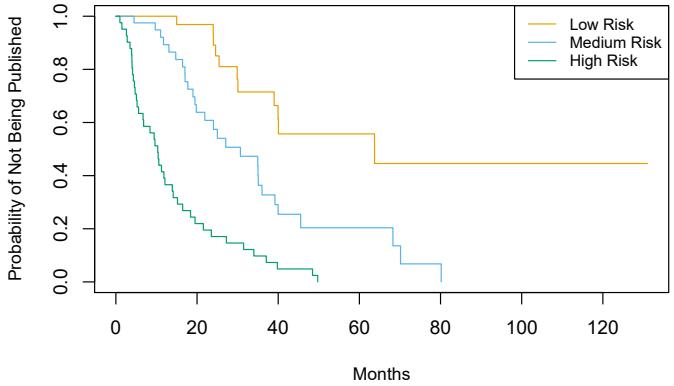
FIGURE 11.8. For the Publication data introduced in Section 11.5.4, we compute tertiles of “risk” in the test set using coefcients estimated on the training set. There is clear separation between the resulting survival curves.
the (possibly-censored) times y1,…,yn, as well as the censoring indicators δ1,…, δn.
Therefore, Harrell’s concordance index (or C-index) computes the pro- Harrell’s portion of observation pairs for which ηˆi′ > ηˆi and yi > yi′ :
concordance index
\[C = \frac{\sum\_{i,i':y\_i>y\_{i'}} I(\hat{\eta}\_{i'} > \hat{\eta}\_i) \delta\_{i'}}{\sum\_{i,i':y\_i>y\_{i'}} \delta\_{i'}},\]
where the indicator variable I(ˆηi′ > ηˆi) equals one if ηˆi′ > ηˆi, and equals zero otherwise. The numerator and denominator are multiplied by the status indicator δi′ , since if the i ′ th observation is uncensored (i.e. if δi′ = 1), then yi > yi′ implies that ti > ti′ . By contrast, if δi′ = 0, then yi > yi′ does not imply that ti > ti′ .
We ft a Cox proportional hazards model on the training set of the Publication data, and computed the C-index on the test set. This yielded C = 0.733. Roughly speaking, given two random papers from the test set, the model can predict with 73.3% accuracy which will be published frst.
11.7.2 Choice of Time Scale
In the examples considered thus far in this chapter, it has been fairly clear how to defne time. For example, in the Publication example, time zero for each paper was defned to be the calendar time at the end of the study, and the failure time was defned to be the number of months that elapsed from the end of the study until the paper was published.
However, in other settings, the defnitions of time zero and failure time may be more subtle. For example, when examining the association between risk factors and disease occurrence in an epidemiological study, one might use the patient’s age to defne time, so that time zero is the patient’s date of birth. With this choice, the association between age and survival cannot be measured; however, there is no need to adjust for age in the analysis. When examining covariates associated with disease-free survival (i.e. the amount of time elapsed between treatment and disease recurrence), one might use the date of treatment as time zero.
11.7.3 Time-Dependent Covariates
A powerful feature of the proportional hazards model is its ability to handle time-dependent covariates, predictors whose value may change over time. For example, suppose we measure a patient’s blood pressure every week over the course of a medical study. In this case, we can think of the blood pressure for the ith observation not as xi, but rather as xi(t) at time t.
Because the partial likelihood in (11.16) is constructed sequentially in time, dealing with time-dependent covariates is straightforward. In particular, we simply replace xij and xi′j in (11.16) with xij (yi) and xi′j (yi), respectively; these are the current values of the predictors at time yi. By contrast, time-dependent covariates would pose a much greater challenge within the context of a traditional parametric approach, such as (11.13).
One example of time-dependent covariates appears in the analysis of data from the Stanford Heart Transplant Program. Patients in need of a heart transplant were put on a waiting list. Some patients received a transplant, but others died while still on the waiting list. The primary objective of the analysis was to determine whether a transplant was associated with longer patient survival.
A naïve approach would use a fxed covariate to represent transplant status: that is, xi = 1 if the ith patient ever received a transplant, and xi = 0 otherwise. But this approach overlooks the fact that patients had to live long enough to get a transplant, and hence, on average, healthier patients received transplants. This problem can be solved by using a time-dependent covariate for transplant: xi(t)=1 if the patient received a transplant by time t, and xi(t)=0 otherwise.
11.7.4 Checking the Proportional Hazards Assumption
We have seen that Cox’s proportional hazards model relies on the proportional hazards assumption (11.14). While results from the Cox model tend to be fairly robust to violations of this assumption, it is still a good idea to check whether it holds. In the case of a qualitative feature, we can plot the log hazard function for each level of the feature. If (11.14) holds, then the log hazard functions should just difer by a constant, as seen in the top-left panel of Figure 11.4. In the case of a quantitative feature, we can take a similar approach by stratifying the feature.
11.7.5 Survival Trees
In Chapter 8, we discussed fexible and adaptive learning procedures such as trees, random forests, and boosting, which we applied in both the regression and classifcation settings. Most of these approaches can be generalized to the survival analysis setting. For example, survival trees are a modifcation survival trees of classifcation and regression trees that use a split criterion that maximizes
the diference between the survival curves in the resulting daughter nodes. Survival trees can then be used to create random survival forests.
11.8 Lab: Survival Analysis
In this lab, we perform survival analyses on three separate data sets. In Section 11.8.1 we analyze the BrainCancer data that was frst described in Section 11.3. In Section 11.8.2, we examine the Publication data from Section 11.5.4. Finally, Section 11.8.3 explores a simulated call-center data set.
We begin by importing some of our libraries at this top level. This makes the code more readable, as scanning the frst few lines of the notebook tell us what libraries are used in this notebook.
In [1]: from matplotlib.pyplot import subplots
import numpy as np
import pandas as pd
from ISLP.models import ModelSpec as MS
from ISLP import load_dataWe also collect the new imports needed for this lab.
In [2]: from lifelines import \
(KaplanMeierFitter,
CoxPHFitter)
from lifelines.statistics import \
(logrank_test,
multivariate_logrank_test)
from ISLP.survival import sim_time11.8.1 Brain Cancer Data
We begin with the BrainCancer data set, contained in the ISLP package.
In [3]: BrainCancer = load_data('BrainCancer')
BrainCancer.columnsOut[3]: Index(['sex', 'diagnosis', 'loc', 'ki', 'gtv', 'stereo',
'status', 'time'],
dtype='object')The rows index the 88 patients, while the 8 columns contain the predictors and outcome variables. We frst briefy examine the data.
In [4]: BrainCancer['sex'].value_counts()Out[4]: Female 45
Male 43
Name: sex, dtype: int64
In [5]: BrainCancer['diagnosis'].value_counts()490 11. Survival Analysis and Censored Data
Out[5]: Meningioma 42
HG glioma 22
Other 14
LG glioma 9
Name: diagnosis, dtype: int64In [6]: BrainCancer['status'].value_counts()Out[6]: 0 53 1 35
Name: status, dtype: int64
Before beginning an analysis, it is important to know how the status variable has been coded. Most software uses the convention that a status of 1 indicates an uncensored observation (often death), and a status of 0 indicates a censored observation. But some scientists might use the opposite coding. For the BrainCancer data set 35 patients died before the end of the study, so we are using the conventional coding.
To begin the analysis, we re-create the Kaplan-Meier survival curve shown in Figure 11.2. The main package we will use for survival analysis is lifelines. The variable time corresponds to yi, the time to the ith lifelines event (either censoring or death). The frst argument to km.fit is the event time, and the second argument is the censoring variable, with a 1 indicating an observed failure time. The plot() method produces a survival curve .plot() with pointwise confdence intervals. By default, these are 90% confdence intervals, but this can be changed by setting the alpha argument to one minus the desired confdence level.
In [7]: fig, ax = subplots(figsize=(8,8))
km = KaplanMeierFitter()
km_brain = km.fit(BrainCancer['time'], BrainCancer['status'])
km_brain.plot(label='Kaplan Meier estimate', ax=ax)Next we create Kaplan-Meier survival curves that are stratifed by sex, in order to reproduce Figure 11.3. We do this using the groupby() method of .groupby() a dataframe. This method returns a generator that can be iterated over in the for loop. In this case, the items in the for loop are 2-tuples representing the groups: the frst entry is the value of the grouping column sex while the second value is the dataframe consisting of all rows in the dataframe matching that value of sex. We will want to use this data below in the logrank test, hence we store this information in the dictionary by_sex. Finally, we have also used the notion of string interpolation to automatically label string interpolation the diferent lines in the plot. String interpolation is a powerful technique to format strings — Python has many ways to facilitate such operations.
In [8]: fig, ax = subplots(figsize=(8,8))
by_sex = {}
for sex, df in BrainCancer.groupby('sex'):
by_sex[sex] = df
km_sex = km.fit(df['time'], df['status'])
km_sex.plot(label='Sex=%s' % sex, ax=ax)As discussed in Section 11.4, we can perform a log-rank test to compare the survival of males to females. We use the logrank_test() function from logrank_
test()
the lifelines.statistics module. The frst two arguments are the event times, with the second denoting the corresponding (optional) censoring indicators.
In [9]: logrank_test(by_sex['Male']['time'],
by_sex['Female']['time'],
by_sex['Male']['status'],
by_sex['Female']['status'])Out[9]: t_0 -1 null_distribution chi squared degrees_of_freedom 1 test_name logrank_test test_statistic p -log2(p) 1.44 0.23 2.12
The resulting p-value is 0.23, indicating no evidence of a diference in survival between the two sexes.
Next, we use the CoxPHFitter() estimator from lifelines to ft Cox CoxPHFitter() proportional hazards models. To begin, we consider a model that uses sex as the only predictor.
In [10]: coxph = CoxPHFitter # shorthand
sex_df = BrainCancer[['time', 'status', 'sex']]
model_df = MS(['time', 'status', 'sex'],
intercept=False).fit_transform(sex_df)
cox_fit = coxph().fit(model_df,
'time',
'status')
cox_fit.summary[['coef', 'se(coef)', 'p']]Out[10]: coef se(coef) p
covariate
sex[Male] 0.407667 0.342004 0.233263The frst argument to fit should be a data frame containing at least the event time (the second argument time in this case), as well as an optional censoring variable (the argument status in this case). Note also that the Cox model does not include an intercept, which is why we used the intercept=False argument to ModelSpec above. The summary() method delivers many columns; we chose to abbreviate its output here. It is possible to obtain the likelihood ratio test comparing this model to the one with no features as follows:
In [11]: cox_fit.log_likelihood_ratio_test()
Out[11]: null_distribution chi squared
degrees_freedom 1
test_name log-likelihood ratio test
test_statistic p -log2(p)
1.44 0.23 2.12Regardless of which test we use, we see that there is no clear evidence for a diference in survival between males and females. As we learned in this chapter, the score test from the Cox model is exactly equal to the log rank test statistic!
Now we ft a model that makes use of additional predictors. We frst note that one of our diagnosis values is missing, hence we drop that observation before continuing.
In [12]: cleaned = BrainCancer.dropna()
all_MS = MS(cleaned.columns, intercept=False)
all_df = all_MS.fit_transform(cleaned)
fit_all = coxph().fit(all_df,
'time',
'status')
fit_all.summary[['coef', 'se(coef)', 'p']]Out[12]: coef se(coef) p
| C | f | ) | ||
|---|---|---|---|---|
| C | oe |
| covariate | |||
|---|---|---|---|
| sex[Male] | 0.183748 | 0.360358 | 0.610119 |
| diagnosis[LG glioma] |
-1.239541 | 0.579557 | 0.032454 |
| diagnosis[Meningioma] | -2.154566 | 0.450524 | 0.000002 |
| diagnosis[Other] | -1.268870 | 0.617672 | 0.039949 |
| loc[Supratentorial] | 0.441195 | 0.703669 | 0.530664 |
| ki | -0.054955 | 0.018314 | 0.002693 |
| gtv | 0.034293 | 0.022333 | 0.124660 |
| stereo[SRT] | 0.177778 | 0.601578 | 0.767597 |
The diagnosis variable has been coded so that the baseline corresponds to HG glioma. The results indicate that the risk associated with HG glioma is more than eight times (i.e. e2.15 = 8.62) the risk associated with meningioma. In other words, after adjusting for the other predictors, patients with HG glioma have much worse survival compared to those with meningioma. In addition, larger values of the Karnofsky index, ki, are associated with lower risk, i.e. longer survival.
Finally, we plot estimated survival curves for each diagnosis category, adjusting for the other predictors. To make these plots, we set the values of the other predictors equal to the mean for quantitative variables and equal to the mode for categorical. To do this, we use the apply() method across rows (i.e. axis=0) with a function representative that checks if a column is categorical or not.
In [13]: levels = cleaned['diagnosis'].unique()
def representative(series):
if hasattr(series.dtype, 'categories'):
return pd.Series.mode(series)
else:
return series.mean()
modal_data = cleaned.apply(representative, axis=0)We make four copies of the column means and assign the diagnosis column to be the four diferent diagnoses.
In [14]: modal_df = pd.DataFrame(
[modal_data.iloc[0] for _ in range(len(levels))])
modal_df['diagnosis'] = levels
modal_dfOut[14]: sex diagnosis loc ki gtv stereo ...
Female Meningioma Supratentorial 80.920 8.687 SRT ...
Female HG glioma Supratentorial 80.920 8.687 SRT ...
Female LG glioma Supratentorial 80.920 8.687 SRT ...
Female Other Supratentorial 80.920 8.687 SRT ...We then construct the model matrix based on the model specifcation all_MS used to ft the model, and name the rows according to the levels of diagnosis.
In [15]: modal_X = all_MS.transform(modal_df)
modal_X.index = levels
modal_XWe can use the predict_survival_function() method to obtain the esti- .predict_ mated survival function.
In [16]: predicted_survival = fit_all.predict_survival_function(modal_X)
predicted_survivalsurvival_ function()
| Out[16]: | Meningioma | HG | glioma | LG | glioma | Other |
|---|---|---|---|---|---|---|
| 0.070 | 0.998 | 0.982 | 0.995 | 0.995 | ||
| 1.180 | 0.998 | 0.982 | 0.995 | 0.995 | ||
| 1.410 | 0.996 | 0.963 | 0.989 | 0.990 | ||
| 1.540 | 0.996 | 0.963 | 0.989 | 0.990 | ||
| 67.380 | 0.689 | 0.040 | 0.394 | 0.405 | ||
| 73.740 | 0.689 | 0.040 | 0.394 | 0.405 | ||
| 78.750 | 0.689 | 0.040 | 0.394 | 0.405 | ||
| 82.560 | 0.689 | 0.040 | 0.394 | 0.405 | ||
| 85 | rows × 4 |
columns |
This returns a data frame, whose plot methods yields the diferent survival curves. To avoid clutter in the plots, we do not display confdence intervals.
In [17]: fig, ax = subplots(figsize=(8, 8))
predicted_survival.plot(ax=ax);11.8.2 Publication Data
The Publication data presented in Section 11.5.4 can be found in the ISLP package. We frst reproduce Figure 11.5 by plotting the Kaplan-Meier curves stratifed on the posres variable, which records whether the study had a positive or negative result.
In [18]: fig, ax = subplots(figsize=(8,8))
Publication = load_data('Publication')
by_result = {}
for result, df in Publication.groupby('posres'):
by_result[result] = df
km_result = km.fit(df['time'], df['status'])
km_result.plot(label='Result=%d' % result, ax=ax)As discussed previously, the p-values from ftting Cox’s proportional hazards model to the posres variable are quite large, providing no evidence of a diference in time-to-publication between studies with positive versus negative results.
494 11. Survival Analysis and Censored Data
In [19]: posres_df = MS(['posres',
'time',
'status'],
intercept=False).fit_transform(Publication)
posres_fit = coxph().fit(posres_df,
'time',
'status')
posres_fit.summary[['coef', 'se(coef)', 'p']]Out[19]: coef se(coef) p
covariate
posres 0.148076 0.161625 0.359578However, the results change dramatically when we include other predictors in the model. Here we exclude the funding mechanism variable.
In [20]: model = MS(Publication.columns.drop('mech'),
intercept=False)
coxph().fit(model.fit_transform(Publication),
'time',
'status').summary[['coef', 'se(coef)', 'p']]Out[20]: coef se(coef) p
covariate
posres 0.570774 0.175960 1.179606e-03
multi -0.040863 0.251194 8.707727e-01
clinend 0.546180 0.262001 3.710099e-02
sampsize 0.000005 0.000015 7.506978e-01
budget 0.004386 0.002464 7.511276e-02
impact 0.058318 0.006676 2.426779e-18We see that there are a number of statistically signifcant variables, including whether the trial focused on a clinical endpoint, the impact of the study, and whether the study had positive or negative results.
11.8.3 Call Center Data
In this section, we will simulate survival data using the relationship between cumulative hazard and the survival function explored in Exercise 8. Our simulated data will represent the observed wait times (in seconds) for 2,000 customers who have phoned a call center. In this context, censoring occurs if a customer hangs up before his or her call is answered.
There are three covariates: Operators (the number of call center operators available at the time of the call, which can range from 5 to 15), Center (either A, B, or C), and Time of day (Morning, Afternoon, or Evening). We generate data for these covariates so that all possibilities are equally likely: for instance, morning, afternoon and evening calls are equally likely, and any number of operators from 5 to 15 is equally likely.
In [21]: rng = np.random.default_rng(10)N = 2000
Operators = rng.choice(np.arange(5, 16),
N,
replace=True)Center = rng.choice(['A', 'B', 'C'],
N,
replace=True)
Time = rng.choice(['Morn.', 'After.', 'Even.'],
N,
replace=True)
D = pd.DataFrame({'Operators': Operators,
'Center': pd.Categorical(Center),
'Time': pd.Categorical(Time)})We then build a model matrix (omitting the intercept)
In [22]: model = MS(['Operators',
'Center',
'Time'],
intercept=False)
X = model.fit_transform(D)It is worthwhile to take a peek at the model matrix X, so that we can be sure that we understand how the variables have been coded. By default, the levels of categorical variables are sorted and, as usual, the frst column of the one-hot encoding of the variable is dropped.
In [23]: X[:5]
| Out[23]: | Operators | Center[B] | Center[C] | Time[Even.] | Time[Morn.] | |
|---|---|---|---|---|---|---|
| 0 | 13 | 0.0 | 1.0 | 0.0 | 0.0 | |
| 1 | 15 | 0.0 | 0.0 | 1.0 | 0.0 | |
| 2 | 7 | 1.0 | 0.0 | 0.0 | 1.0 | |
| 3 | 7 | 0.0 | 1.0 | 0.0 | 1.0 | |
| 4 | 13 | 0.0 | 1.0 | 1.0 | 0.0 |
Next, we specify the coefcients and the hazard function.
In [24]: true_beta = np.array([0.04, -0.3, 0, 0.2, -0.2])
true_linpred = X.dot(true_beta)
hazard = lambda t: 1e-5 * tHere, we have set the coefcient associated with Operators to equal 0.04; in other words, each additional operator leads to a e0.04 = 1.041-fold increase in the “risk” that the call will be answered, given the Center and Time covariates. This makes sense: the greater the number of operators at hand, the shorter the wait time! The coefcient associated with Center == B is −0.3, and Center == A is treated as the baseline. This means that the risk of a call being answered at Center B is 0.74 times the risk that it will be answered at Center A; in other words, the wait times are a bit longer at Center B.
Recall from Section 2.3.7 the use of lambda for creating short functions on the fy. We use the function sim_time() from the ISLP.survival pack- sim_time() age. This function uses the relationship between the survival function and cumulative hazard S(t) = exp(−H(t)) and the specifc form of the cumulative hazard function in the Cox model to simulate data based on values of the linear predictor true_linpred and the cumulative hazard. We need to provide the cumulative hazard function, which we do here.
In [25]: cum_hazard = lambda t: 1e-5 * t**2 / 2
We are now ready to generate data under the Cox proportional hazards model. We truncate the maximum time to 1000 seconds to keep simulated wait times reasonable. The function sim_time() takes a linear predictor, a cumulative hazard function and a random number generator.
In [26]: W = np.array([sim_time(l, cum_hazard, rng)
for l in true_linpred])
D['Wait time'] = np.clip(W, 0, 1000)We now simulate our censoring variable, for which we assume 90% of calls were answered (Failed==1) before the customer hung up (Failed==0).
In [27]: D['Failed'] = rng.choice([1, 0],
N,
p=[0.9, 0.1])
D[:5]
Out[27]: Operators Center Time Wait time Failed
0 13 C After. 525.064979 1
1 15 A Even. 254.677835 1
2 7 B Morn. 487.739224 1
3 7 C Morn. 308.580292 1
4 13 C Even. 154.174608 1
In [28]: D['Failed'].mean()Out[28]: 0.8985
We now plot Kaplan-Meier survival curves. First, we stratify by Center.
In [29]: fig, ax = subplots(figsize=(8,8))
by_center = {}
for center, df in D.groupby('Center'):
by_center[center] = df
km_center = km.fit(df['Wait time'], df['Failed'])
km_center.plot(label='Center=%s' % center, ax=ax)
ax.set_title("Probability of Still Being on Hold")Next, we stratify by Time.
In [30]: fig, ax = subplots(figsize=(8,8))
by_time = {}
for time, df in D.groupby('Time'):
by_time[time] = df
km_time = km.fit(df['Wait time'], df['Failed'])
km_time.plot(label='Time=%s' % time, ax=ax)
ax.set_title("Probability of Still Being on Hold")It seems that calls at Call Center B take longer to be answered than calls at Centers A and C. Similarly, it appears that wait times are longest in the morning and shortest in the evening hours. We can use a log-rank test to determine whether these diferences are statistically signifcant using the function multivariate_logrank_test().
In [31]: multivariate_logrank_test(D['Wait time'],
D['Center'],
D['Failed'])Out[31]: t_0 -1
null_distribution chi squared
degrees_of_freedom 2
test_name multivariate_logrank_test
test_statistic p -log2(p)
20.30 <0.005 14.65Next, we consider the efect of Time.
In [32]: multivariate_logrank_test(D['Wait time'],
D['Time'],
D['Failed'])Out[32]: t_0 -1
null_distribution chi squared
degrees_of_freedom 2
test_name multivariate_logrank_test
test_statistic p -log2(p)
49.90 <0.005 35.99As in the case of a categorical variable with 2 levels, these results are similar to the likelihood ratio test from the Cox proportional hazards model. First, we look at the results for Center.
In [33]: X = MS(['Wait time',
'Failed',
'Center'],
intercept=False).fit_transform(D)
F = coxph().fit(X, 'Wait time', 'Failed')
F.log_likelihood_ratio_test()Out[33]: null_distribution chi squared
degrees_freedom 2
test_name log-likelihood ratio test
test_statistic p -log2(p)
20.58 <0.005 14.85Next, we look at the results for Time.
In [34]: X = MS(['Wait time',
'Failed',
'Time'],
intercept=False).fit_transform(D)
F = coxph().fit(X, 'Wait time', 'Failed')
F.log_likelihood_ratio_test()Out[34]: null_distribution chi squared
degrees_freedom 2
test_name log-likelihood ratio test
test_statistic p -log2(p)
48.12 <0.005 34.71We fnd that diferences between centers are highly signifcant, as are diferences between times of day.
Finally, we ft Cox’s proportional hazards model to the data.
498 11. Survival Analysis and Censored Data
In [35]: X = MS(D.columns,intercept=False).fit_transform(D)
fit_queuing = coxph().fit(
X,
'Wait time',
'Failed')
fit_queuing.summary[['coef', 'se(coef)', 'p']]Out[35]: coef se(coef) p
| covariate | |||
|---|---|---|---|
| Operators | 0.043934 | 0.007520 | 5.143677e-09 |
| Center[B] | -0.236059 | 0.058113 | 4.864734e-05 |
| Center[C] | 0.012231 | 0.057518 | 8.316083e-01 |
| Time[Even.] | 0.268845 | 0.057797 | 3.294914e-06 |
| Time[Morn.] | -0.148215 | 0.057334 | 9.734378e-03 |
The p-values for Center B and evening time are very small. It is also clear that the hazard — that is, the instantaneous risk that a call will be answered — increases with the number of operators. Since we generated the data ourselves, we know that the true coefcients for Operators, Center = B, Center = C, Time = Even. and Time = Morn. are 0.04, −0.3, 0, 0.2, and −0.2, respectively. The coefcient estimates from the ftted Cox model are fairly accurate.
11.9 Exercises
Conceptual
- For each example, state whether or not the censoring mechanism is independent. Justify your answer.
- In a study of disease relapse, due to a careless research scientist, all patients whose phone numbers begin with the number “2” are lost to follow up.
- In a study of longevity, a formatting error causes all patient ages that exceed 99 years to be lost (i.e. we know that those patients are more than 99 years old, but we do not know their exact ages).
- Hospital A conducts a study of longevity. However, very sick patients tend to be transferred to Hospital B, and are lost to follow up.
- In a study of unemployment duration, the people who fnd work earlier are less motivated to stay in touch with study investigators, and therefore are more likely to be lost to follow up.
- In a study of pregnancy duration, women who deliver their babies pre-term are more likely to do so away from their usual hospital, and thus are more likely to be censored, relative to women who deliver full-term babies.
- A researcher wishes to model the number of years of education of the residents of a small town. Residents who enroll in college out of town are more likely to be lost to follow up, and are also more likely to attend graduate school, relative to those who attend college in town.
- Researchers conduct a study of disease-free survival (i.e. time until disease relapse following treatment). Patients who have not relapsed within fve years are considered to be cured, and thus their survival time is censored at fve years.
- We wish to model the failure time for some electrical component. This component can be manufactured in Iowa or in Pittsburgh, with no diference in quality. The Iowa factory opened fve years ago, and so components manufactured in Iowa are censored at fve years. The Pittsburgh factory opened two years ago, so those components are censored at two years.
- We wish to model the failure time of an electrical component made in two diferent factories, one of which opened before the other. We have reason to believe that the components manufactured in the factory that opened earlier are of higher quality.
- We conduct a study with n = 4 participants who have just purchased cell phones, in order to model the time until phone replacement. The frst participant replaces her phone after 1.2 years. The second participant still has not replaced her phone at the end of the two-year study period. The third participant changes her phone number and is lost to follow up (but has not yet replaced her phone) 1.5 years into the study. The fourth participant replaces her phone after 0.2 years.
For each of the four participants (i = 1,…, 4), answer the following questions using the notation introduced in Section 11.1:
- Is the participant’s cell phone replacement time censored?
- Is the value of ci known, and if so, then what is it?
- Is the value of ti known, and if so, then what is it?
- Is the value of yi known, and if so, then what is it?
- Is the value of δi known, and if so, then what is it?
- This problem makes use of the Kaplan-Meier survival curve displayed in Figure 11.9. The raw data that went into plotting this survival curve is given in Table 11.4. The covariate column of that table is not needed for this problem.
- What is the estimated probability of survival past 50 days?
| Observation (Y ) |
Censoring Indicator (δ) | Covariate (X) |
|---|---|---|
| 26.5 | 1 | 0.1 |
| 37.2 | 1 | 11 |
| 57.3 | 1 | -0.3 |
| 90.8 | 0 | 2.8 |
| 20.2 | 0 | 1.8 |
| 89.8 | 0 | 0.4 |
TABLE 11.4. Data used in Exercise 4.
- Write out an analytical expression for the estimated survival function. For instance, your answer might be something along the lines of
\[ \widehat{S}(t) = \begin{cases} 0.8 & \text{if } t < 31 \\ 0.5 & \text{if } 31 \le t < 77 \\ 0.22 & \text{if } 77 \le t. \end{cases} \]
(The previous equation is for illustration only: it is not the correct answer!)
- Sketch the survival function given by the equation
\[ \widehat{S}(t) = \begin{cases} 0.8 & \text{if } t < 31 \\ 0.5 & \text{if } 31 \le t < 77 \\ 0.22 & \text{if } 77 \le t. \end{cases} \]
Your answer should look something like Figure 11.9.
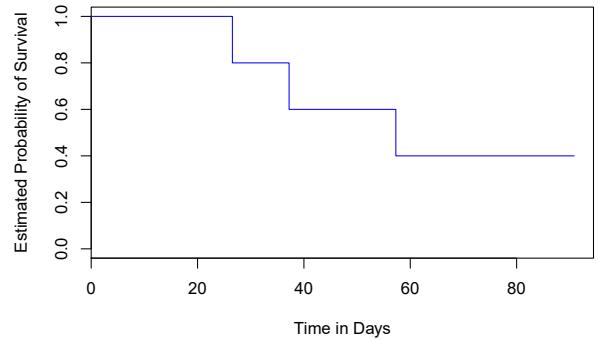
FIGURE 11.9. A Kaplan-Meier survival curve used in Exercise 4.
- Sketch the Kaplan-Meier survival curve corresponding to this data set. (You do not need to use any software to do this — you can sketch it by hand using the results obtained in (a).)
- Based on the survival curve estimated in (b), what is the probability that the event occurs within 200 days? What is the probability that the event does not occur within 310 days?
- Write out an expression for the estimated survival curve from (b).
- In this problem, we will derive (11.5) and (11.6), which are needed for the construction of the log-rank test statistic (11.8). Recall the notation in Table 11.1.
- Assume that there is no diference between the survival functions of the two groups. Then we can think of q1k as the number of failures if we draw r1k observations, without replacement, from a risk set of rk observations that contains a total of qk failures. Argue that q1k follows a hypergeometric distribution. Write the hyperparameters of this distribution in terms of r1k, rk, and qk.
geometric distribution
\[\begin{aligned} f(t) &= -dF(t)/dt\\ S(t) &= -\exp\left(-\int\_0^t h(u)du\right). \end{aligned}\]
- In this exercise, we will explore the consequences of assuming that the survival times follow an exponential distribution.
- Suppose that a survival time follows an Exp(λ) distribution, so that its density function is f(t) = λ exp(−λt). Using the relationships provided in Exercise 8, show that S(t) = exp(−λt).
- Now suppose that each of n independent survival times follows an Exp(λ) distribution. Write out an expression for the likelihood function (11.13).
- Show that the maximum likelihood estimator for λ is
\[ \hat{\lambda} = \sum\_{i=1}^{n} \delta\_i / \sum\_{i=1}^{n} y\_i. \]
- Use your answer to (c) to derive an estimator of the mean survival time.
Hint: For (d), recall that the mean of an Exp(λ) random variable is 1/λ.
Applied
- This exercise focuses on the brain tumor data, which is included in the ISLP library.
- Plot the Kaplan-Meier survival curve with ±1 standard error bands, using the KaplanMeierFitter() estimator in the lifelines package.
- Draw a bootstrap sample of size n = 88 from the pairs (yi, δi), and compute the resulting Kaplan-Meier survival curve. Repeat this process B = 200 times. Use the results to obtain an estimate of the standard error of the Kaplan-Meier survival curve at each timepoint. Compare this to the standard errors obtained in (a).
- Fit a Cox proportional hazards model that uses all of the predictors to predict survival. Summarize the main fndings.
- Stratify the data by the value of ki. (Since only one observation has ki==40, you can group that observation together with the observations that have ki==60.) Plot Kaplan-Meier survival curves for each of the fve strata, adjusted for the other predictors.
- This exercise makes use of the data in Table 11.4.
- Create two groups of observations. In Group 1, X < 2, whereas in Group 2, X ≥ 2. Plot the Kaplan-Meier survival curves corresponding to the two groups. Be sure to label the curves so that it is clear which curve corresponds to which group. By eye, does there appear to be a diference between the two groups’ survival curves?
- Fit Cox’s proportional hazards model, using the group indicator as a covariate. What is the estimated coefcient? Write a sentence providing the interpretation of this coefcient, in terms of the hazard or the instantaneous probability of the event. Is there evidence that the true coefcient value is non-zero?
- Recall from Section 11.5.2 that in the case of a single binary covariate, the log-rank test statistic should be identical to the score statistic for the Cox model. Conduct a log-rank test to determine whether there is a diference between the survival curves for the two groups. How does the p-value for the log-rank test statistic compare to the p-value for the score statistic for the Cox model from (b)?
12 Unsupervised Learning

Most of this book concerns supervised learning methods such as regression and classifcation. In the supervised learning setting, we typically have access to a set of p features X1, X2,…,Xp, measured on n observations, and a response Y also measured on those same n observations. The goal is then to predict Y using X1, X2,…,Xp.
This chapter will instead focus on unsupervised learning, a set of statistical tools intended for the setting in which we have only a set of features X1, X2,…,Xp measured on n observations. We are not interested in prediction, because we do not have an associated response variable Y . Rather, the goal is to discover interesting things about the measurements on X1, X2,…,Xp. Is there an informative way to visualize the data? Can we discover subgroups among the variables or among the observations? Unsupervised learning refers to a diverse set of techniques for answering questions such as these. In this chapter, we will focus on two particular types of unsupervised learning: principal components analysis, a tool used for data visualization or data pre-processing before supervised techniques are applied, and clustering, a broad class of methods for discovering unknown subgroups in data.
12.1 The Challenge of Unsupervised Learning
Supervised learning is a well-understood area. In fact, if you have read the preceding chapters in this book, then you should by now have a good grasp of supervised learning. For instance, if you are asked to predict a binary outcome from a data set, you have a very well developed set of tools at your disposal (such as logistic regression, linear discriminant analysis, classifcation trees, support vector machines, and more) as well as a clear
© Springer Nature Switzerland AG 2023
G. James et al., An Introduction to Statistical Learning, Springer Texts in Statistics, https://doi.org/10.1007/978-3-031-38747-0\_12
understanding of how to assess the quality of the results obtained (using cross-validation, validation on an independent test set, and so forth).
In contrast, unsupervised learning is often much more challenging. The exercise tends to be more subjective, and there is no simple goal for the analysis, such as prediction of a response. Unsupervised learning is often performed as part of an exploratory data analysis. Furthermore, it can be exploratory hard to assess the results obtained from unsupervised learning methods, since there is no universally accepted mechanism for performing crossvalidation or validating results on an independent data set. The reason for this diference is simple. If we ft a predictive model using a supervised learning technique, then it is possible to check our work by seeing how well our model predicts the response Y on observations not used in ftting the model. However, in unsupervised learning, there is no way to check our work because we don’t know the true answer—the problem is unsupervised.
Techniques for unsupervised learning are of growing importance in a number of felds. A cancer researcher might assay gene expression levels in 100 patients with breast cancer. He or she might then look for subgroups among the breast cancer samples, or among the genes, in order to obtain a better understanding of the disease. An online shopping site might try to identify groups of shoppers with similar browsing and purchase histories, as well as items that are of particular interest to the shoppers within each group. Then an individual shopper can be preferentially shown the items in which he or she is particularly likely to be interested, based on the purchase histories of similar shoppers. A search engine might choose which search results to display to a particular individual based on the click histories of other individuals with similar search patterns. These statistical learning tasks, and many more, can be performed via unsupervised learning techniques.
12.2 Principal Components Analysis
Principal components are discussed in Section 6.3.1 in the context of principal components regression. When faced with a large set of correlated variables, principal components allow us to summarize this set with a smaller number of representative variables that collectively explain most of the variability in the original set. The principal component directions are presented in Section 6.3.1 as directions in feature space along which the original data are highly variable. These directions also defne lines and subspaces that are as close as possible to the data cloud. To perform principal components regression, we simply use principal components as predictors in a regression model in place of the original larger set of variables.
Principal components analysis (PCA) refers to the process by which prin- principal cipal components are computed, and the subsequent use of these components in understanding the data. PCA is an unsupervised approach, since it involves only a set of features X1, X2,…,Xp, and no associated response Y . Apart from producing derived variables for use in supervised learning problems, PCA also serves as a tool for data visualization (visualization of
components analysis
the observations or visualization of the variables). It can also be used as a tool for data imputation — that is, for flling in missing values in a data matrix.
We now discuss PCA in greater detail, focusing on the use of PCA as a tool for unsupervised data exploration, in keeping with the topic of this chapter.
12.2.1 What Are Principal Components?
Suppose that we wish to visualize n observations with measurements on a set of p features, X1, X2,…,Xp, as part of an exploratory data analysis. We could do this by examining two-dimensional scatterplots of the data, each of which contains the n observations’ measurements on two of the features. However, there are 5p 2 6 = p(p−1)/2 such scatterplots; for example, with p = 10 there are 45 plots! If p is large, then it will certainly not be possible to look at all of them; moreover, most likely none of them will be informative since they each contain just a small fraction of the total information present in the data set. Clearly, a better method is required to visualize the n observations when p is large. In particular, we would like to fnd a low-dimensional representation of the data that captures as much of the information as possible. For instance, if we can obtain a two-dimensional representation of the data that captures most of the information, then we can plot the observations in this low-dimensional space.
PCA provides a tool to do just this. It fnds a low-dimensional representation of a data set that contains as much as possible of the variation. The idea is that each of the n observations lives in p-dimensional space, but not all of these dimensions are equally interesting. PCA seeks a small number of dimensions that are as interesting as possible, where the concept of interesting is measured by the amount that the observations vary along each dimension. Each of the dimensions found by PCA is a linear combination of the p features. We now explain the manner in which these dimensions, or principal components, are found.
The frst principal component of a set of features X1, X2,…,Xp is the normalized linear combination of the features
\[Z\_1 = \phi\_{11} X\_1 + \phi\_{21} X\_2 + \dots + \phi\_{p1} X\_p \tag{12.1}\]
that has the largest variance. By normalized, we mean that #p j=1 φ2 j1 = 1. We refer to the elements φ11,…, φp1 as the loadings of the frst principal loading component; together, the loadings make up the principal component loading vector, φ1 = (φ11 φ21 … φp1)T . We constrain the loadings so that their sum of squares is equal to one, since otherwise setting these elements to be arbitrarily large in absolute value could result in an arbitrarily large variance.
Given an n × p data set X, how do we compute the frst principal component? Since we are only interested in variance, we assume that each of the variables in X has been centered to have mean zero (that is, the column means of X are zero). We then look for the linear combination of the sample feature values of the form
\[z\_{i1} = \phi\_{11} x\_{i1} + \phi\_{21} x\_{i2} + \dots + \phi\_{p1} x\_{ip} \tag{12.2}\]
that has largest sample variance, subject to the constraint that #p j=1 φ2 j1=1. In other words, the frst principal component loading vector solves the optimization problem
\[\underset{\phi\_{11},...,\phi\_{p1}}{\text{maximize}} \left\{ \frac{1}{n} \sum\_{i=1}^{n} \left( \sum\_{j=1}^{p} \phi\_{j1} x\_{ij} \right)^{2} \right\} \text{ subject to } \sum\_{j=1}^{p} \phi\_{j1}^{2} = 1. \tag{12.3}\]
From (12.2) we can write the objective in (12.3) as 1 n #n i=1 z2 i1. Since 1 n #n i=1 xij = 0, the average of the z11,…,zn1 will be zero as well. Hence the objective that we are maximizing in (12.3) is just the sample variance of the n values of zi1. We refer to z11,…,zn1 as the scores of the frst princi- score pal component. Problem (12.3) can be solved via an eigen decomposition, eigen decomposition a standard technique in linear algebra, but the details are outside of the scope of this book.1
There is a nice geometric interpretation of the frst principal component. The loading vector φ1 with elements φ11, φ21,…, φp1 defnes a direction in feature space along which the data vary the most. If we project the n data points x1,…,xn onto this direction, the projected values are the principal component scores z11,…,zn1 themselves. For instance, Figure 6.14 on page 254 displays the frst principal component loading vector (green solid line) on an advertising data set. In these data, there are only two features, and so the observations as well as the frst principal component loading vector can be easily displayed. As can be seen from (6.19), in that data set φ11 = 0.839 and φ21 = 0.544.
After the frst principal component Z1 of the features has been determined, we can fnd the second principal component Z2. The second principal component is the linear combination of X1,…,Xp that has maximal variance out of all linear combinations that are uncorrelated with Z1. The second principal component scores z12, z22,…,zn2 take the form
\[z\_{i2} = \phi\_{12}x\_{i1} + \phi\_{22}x\_{i2} + \dots + \phi\_{p2}x\_{ip},\tag{12.4}\]
where φ2 is the second principal component loading vector, with elements φ12, φ22,…, φp2. It turns out that constraining Z2 to be uncorrelated with Z1 is equivalent to constraining the direction φ2 to be orthogonal (perpendicular) to the direction φ1. In the example in Figure 6.14, the observations lie in two-dimensional space (since p = 2), and so once we have found φ1, there is only one possibility for φ2, which is shown as a blue dashed line. (From Section 6.3.1, we know that φ12 = 0.544 and φ22 = −0.839.) But in a larger data set with p > 2 variables, there are multiple distinct principal components, and they are defned in a similar manner. To fnd φ2, we solve a problem similar to (12.3) with φ2 replacing φ1, and with the additional constraint that φ2 is orthogonal to φ1. 2
1As an alternative to the eigen decomposition, a related technique called the singular value decomposition can be used. This will be explored in the lab at the end of this chapter.
2On a technical note, the principal component directions φ1, φ2, φ3,… are given by the ordered sequence of eigenvectors of the matrix XT X, and the variances of the components are the eigenvalues. There are at most min(n − 1, p) principal components.
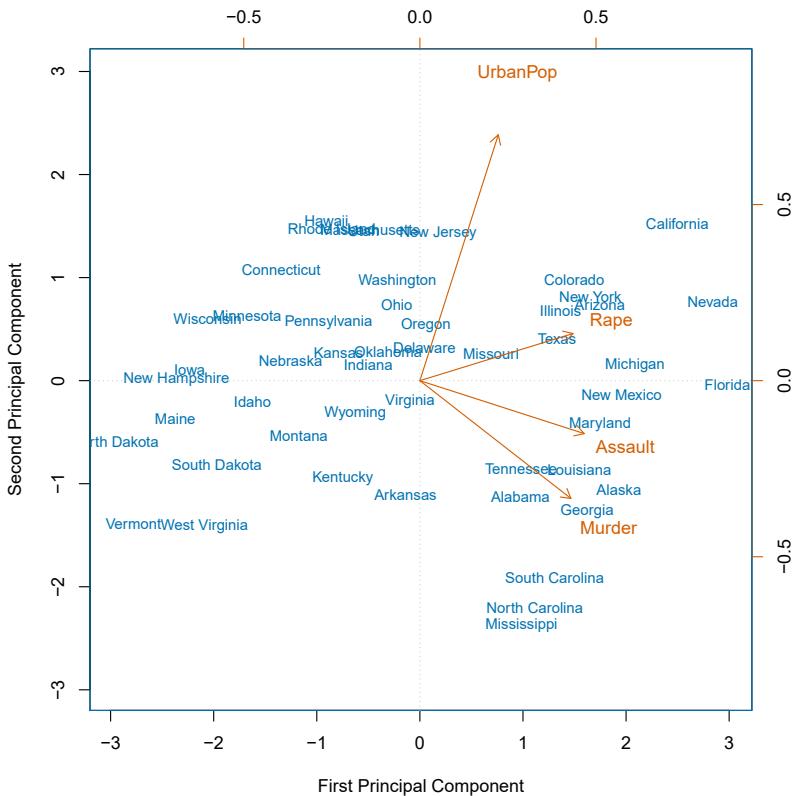
FIGURE 12.1. The frst two principal components for the USArrests data. The blue state names represent the scores for the frst two principal components. The orange arrows indicate the frst two principal component loading vectors (with axes on the top and right). For example, the loading for Rape on the frst component is 0.54, and its loading on the second principal component 0.17 (the word Rape is centered at the point (0.54, 0.17)). This fgure is known as a biplot, because it displays both the principal component scores and the principal component loadings.
Once we have computed the principal components, we can plot them against each other in order to produce low-dimensional views of the data. For instance, we can plot the score vector Z1 against Z2, Z1 against Z3, Z2 against Z3, and so forth. Geometrically, this amounts to projecting the original data down onto the subspace spanned by φ1, φ2, and φ3, and plotting the projected points.
We illustrate the use of PCA on the USArrests data set. For each of the 50 states in the United States, the data set contains the number of arrests per 100, 000 residents for each of three crimes: Assault, Murder, and Rape. We also record UrbanPop (the percent of the population in each state living in urban areas). The principal component score vectors have length n = 50, and the principal component loading vectors have length p = 4. PCA was performed after standardizing each variable to have mean zero and standard
| PC1 | PC2 | |
|---|---|---|
| Murder | 0.5358995 | −0.4181809 |
| Assault | 0.5831836 | −0.1879856 |
| UrbanPop | 0.2781909 | 0.8728062 |
| Rape | 0.5434321 | 0.1673186 |
TABLE 12.1. The principal component loading vectors, φ1 and φ2, for the USArrests data. These are also displayed in Figure 12.1.
deviation one. Figure 12.1 plots the frst two principal components of these data. The fgure represents both the principal component scores and the loading vectors in a single biplot display. The loadings are also given in biplot Table 12.2.1.
In Figure 12.1, we see that the frst loading vector places approximately equal weight on Assault, Murder, and Rape, but with much less weight on UrbanPop. Hence this component roughly corresponds to a measure of overall rates of serious crimes. The second loading vector places most of its weight on UrbanPop and much less weight on the other three features. Hence, this component roughly corresponds to the level of urbanization of the state. Overall, we see that the crime-related variables (Murder, Assault, and Rape) are located close to each other, and that the UrbanPop variable is far from the other three. This indicates that the crime-related variables are correlated with each other—states with high murder rates tend to have high assault and rape rates—and that the UrbanPop variable is less correlated with the other three.
We can examine diferences between the states via the two principal component score vectors shown in Figure 12.1. Our discussion of the loading vectors suggests that states with large positive scores on the frst component, such as California, Nevada and Florida, have high crime rates, while states like North Dakota, with negative scores on the frst component, have low crime rates. California also has a high score on the second component, indicating a high level of urbanization, while the opposite is true for states like Mississippi. States close to zero on both components, such as Indiana, have approximately average levels of both crime and urbanization.
12.2.2 Another Interpretation of Principal Components
The frst two principal component loading vectors in a simulated threedimensional data set are shown in the left-hand panel of Figure 12.2; these two loading vectors span a plane along which the observations have the highest variance.
In the previous section, we describe the principal component loading vectors as the directions in feature space along which the data vary the most, and the principal component scores as projections along these directions. However, an alternative interpretation of principal components can also be
FIGURE 12.2. Ninety observations simulated in three dimensions. The observations are displayed in color for ease of visualization. Left: the frst two principal component directions span the plane that best fts the data. The plane is positioned to minimize the sum of squared distances to each point. Right: the frst two principal component score vectors give the coordinates of the projection of the 90 observations onto the plane.
useful: principal components provide low-dimensional linear surfaces that are closest to the observations. We expand upon that interpretation here.3
The frst principal component loading vector has a very special property: it is the line in p-dimensional space that is closest to the n observations (using average squared Euclidean distance as a measure of closeness). This interpretation can be seen in the left-hand panel of Figure 6.15; the dashed lines indicate the distance between each observation and the line defned by the frst principal component loading vector. The appeal of this interpretation is clear: we seek a single dimension of the data that lies as close as possible to all of the data points, since such a line will likely provide a good summary of the data.
The notion of principal components as the dimensions that are closest to the n observations extends beyond just the frst principal component. For instance, the frst two principal components of a data set span the plane that is closest to the n observations, in terms of average squared Euclidean distance. An example is shown in the left-hand panel of Figure 12.2. The frst three principal components of a data set span the three-dimensional hyperplane that is closest to the n observations, and so forth.
Using this interpretation, together the frst M principal component score vectors and the frst M principal component loading vectors provide the best M-dimensional approximation (in terms of Euclidean distance) to
3In this section, we continue to assume that each column of the data matrix X has been centered to have mean zero—that is, the column mean has been subtracted from each column.
510 12. Unsupervised Learning
the ith observation xij . This representation can be written as
\[x\_{ij} \approx \sum\_{m=1}^{M} z\_{im} \phi\_{jm}.\tag{12.5}\]
We can state this more formally by writing down an optimization problem. Suppose the data matrix X is column-centered. Out of all approximations of the form xij ≈ #M m=1 aimbjm, we could ask for the one with the smallest residual sum of squares:
\[\underset{\mathbf{A}\in\mathbb{R}^{n\times M},\mathbf{B}\in\mathbb{R}^{p\times M}}{\text{minimize}}\left\{\sum\_{j=1}^{p}\sum\_{i=1}^{n}\left(x\_{ij}-\sum\_{m=1}^{M}a\_{im}b\_{jm}\right)^{2}\right\}.\tag{12.6}\]
Here, A is an n × M matrix whose (i, m) element is aim, and B is a p × M element whose (j, m) element is bjm.
It can be shown that for any value of M, the columns of the matrices Aˆ and Bˆ that solve (12.6) are in fact the frst M principal components score and loading vectors. In other words, if Aˆ and Bˆ solve (12.6), then aˆim = zim and ˆbjm = φjm. 4 This means that the smallest possible value of the objective in (12.6) is
\[\sum\_{j=1}^{p} \sum\_{i=1}^{n} \left( x\_{ij} - \sum\_{m=1}^{M} z\_{im} \phi\_{jm} \right)^{2}. \tag{12.7}\]
In summary, together the M principal component score vectors and M principal component loading vectors can give a good approximation to the data when M is sufciently large. When M = min(n − 1, p), then the representation is exact: xij = #M m=1 zimφjm.
12.2.3 The Proportion of Variance Explained
In Figure 12.2, we performed PCA on a three-dimensional data set (lefthand panel) and projected the data onto the frst two principal component loading vectors in order to obtain a two-dimensional view of the data (i.e. the principal component score vectors; right-hand panel). We see that this two-dimensional representation of the three-dimensional data does successfully capture the major pattern in the data: the orange, green, and cyan observations that are near each other in three-dimensional space remain nearby in the two-dimensional representation. Similarly, we have seen on the USArrests data set that we can summarize the 50 observations and 4 variables using just the frst two principal component score vectors and the frst two principal component loading vectors.
We can now ask a natural question: how much of the information in a given data set is lost by projecting the observations onto the frst few principal components? That is, how much of the variance in the data is not contained in the frst few principal components? More generally, we are interested in knowing the proportion of variance explained (PVE) by each proportion
of variance
4Technically, the solution to ( explained 12.6) is not unique. Thus, it is more precise to state that any solution to (12.6) can be easily transformed to yield the principal components.
principal component. The total variance present in a data set (assuming that the variables have been centered to have mean zero) is defned as
\[\sum\_{j=1}^{p} \text{Var}(X\_j) = \sum\_{j=1}^{p} \frac{1}{n} \sum\_{i=1}^{n} x\_{ij}^2,\tag{12.8}\]
and the variance explained by the mth principal component is
\[\frac{1}{n}\sum\_{i=1}^{n}z\_{im}^{2} = \frac{1}{n}\sum\_{i=1}^{n}\left(\sum\_{j=1}^{p}\phi\_{jm}x\_{ij}\right)^{2}.\tag{12.9}\]
Therefore, the PVE of the mth principal component is given by
\[\frac{\sum\_{i=1}^{n} z\_{im}^{2}}{\sum\_{j=1}^{p} \sum\_{i=1}^{n} x\_{ij}^{2}} = \frac{\sum\_{i=1}^{n} \left(\sum\_{j=1}^{p} \phi\_{jm} x\_{ij}\right)^{2}}{\sum\_{j=1}^{p} \sum\_{i=1}^{n} x\_{ij}^{2}}.\tag{12.10}\]
The PVE of each principal component is a positive quantity. In order to compute the cumulative PVE of the frst M principal components, we can simply sum (12.10) over each of the frst M PVEs. In total, there are min(n − 1, p) principal components, and their PVEs sum to one.
In Section 12.2.2, we showed that the frst M principal component loading and score vectors can be interpreted as the best M-dimensional approximation to the data, in terms of residual sum of squares. It turns out that the variance of the data can be decomposed into the variance of the frst M principal components plus the mean squared error of this M-dimensional approximation, as follows:
\[\underbrace{\sum\_{j=1}^{p} \frac{1}{n} \sum\_{i=1}^{n} x\_{ij}^{2}}\_{\text{Var. of data}} = \underbrace{\sum\_{m=1}^{M} \frac{1}{n} \sum\_{i=1}^{n} z\_{im}^{2}}\_{\text{Var. of first } M \text{ PCs}} + \underbrace{\frac{1}{n} \sum\_{j=1}^{p} \sum\_{i=1}^{n} \left( x\_{ij} - \sum\_{m=1}^{M} z\_{im} \phi\_{jm} \right)^{2}}\_{\text{MSE of } M \text{ -dimensional approximator}} \tag{12.11}\]
The three terms in this decomposition are discussed in (12.8), (12.9), and (12.7), respectively. Since the frst term is fxed, we see that by maximizing the variance of the frst M principal components, we minimize the mean squared error of the M-dimensional approximation, and vice versa. This explains why principal components can be equivalently viewed as minimizing the approximation error (as in Section 12.2.2) or maximizing the variance (as in Section 12.2.1).
Moreover, we can use (12.11) to see that the PVE defned in (12.10) equals
\[1 - \frac{\sum\_{j=1}^{p} \sum\_{i=1}^{n} \left( x\_{ij} - \sum\_{m=1}^{M} z\_{im} \phi\_{jm} \right)^2}{\sum\_{j=1}^{p} \sum\_{i=1}^{n} x\_{ij}^2} = 1 - \frac{\text{RSS}}{\text{TSS}},\]
where TSS represents the total sum of squared elements of X, and RSS represents the residual sum of squares of the M-dimensional approximation given by the principal components. Recalling the defnition of R2 from (3.17), this means that we can interpret the PVE as the R2 of the approximation for X given by the frst M principal components.
FIGURE 12.3. Left: a scree plot depicting the proportion of variance explained by each of the four principal components in the USArrests data. Right: the cumulative proportion of variance explained by the four principal components in the USArrests data.
In the USArrests data, the frst principal component explains 62.0 % of the variance in the data, and the next principal component explains 24.7 % of the variance. Together, the frst two principal components explain almost 87 % of the variance in the data, and the last two principal components explain only 13 % of the variance. This means that Figure 12.1 provides a pretty accurate summary of the data using just two dimensions. The PVE of each principal component, as well as the cumulative PVE, is shown in Figure 12.3. The left-hand panel is known as a scree plot, and will be scree plot discussed later in this chapter.
12.2.4 More on PCA
Scaling the Variables
We have already mentioned that before PCA is performed, the variables should be centered to have mean zero. Furthermore, the results obtained when we perform PCA will also depend on whether the variables have been individually scaled (each multiplied by a diferent constant). This is in contrast to some other supervised and unsupervised learning techniques, such as linear regression, in which scaling the variables has no efect. (In linear regression, multiplying a variable by a factor of c will simply lead to multiplication of the corresponding coefcient estimate by a factor of 1/c, and thus will have no substantive efect on the model obtained.)
For instance, Figure 12.1 was obtained after scaling each of the variables to have standard deviation one. This is reproduced in the left-hand plot in Figure 12.4. Why does it matter that we scaled the variables? In these data, the variables are measured in diferent units; Murder, Rape, and Assault are reported as the number of occurrences per 100, 000 people, and UrbanPop is the percentage of the state’s population that lives in an urban area. These four variables have variances of 18.97, 87.73, 6945.16, and 209.5, respectively. Consequently, if we perform PCA on the unscaled variables, then
FIGURE 12.4. Two principal component biplots for the USArrests data. Left: the same as Figure 12.1, with the variables scaled to have unit standard deviations. Right: principal components using unscaled data. Assault has by far the largest loading on the frst principal component because it has the highest variance among the four variables. In general, scaling the variables to have standard deviation one is recommended.
the frst principal component loading vector will have a very large loading for Assault, since that variable has by far the highest variance. The righthand plot in Figure 12.4 displays the frst two principal components for the USArrests data set, without scaling the variables to have standard deviation one. As predicted, the frst principal component loading vector places almost all of its weight on Assault, while the second principal component loading vector places almost all of its weight on UrbanPop. Comparing this to the left-hand plot, we see that scaling does indeed have a substantial efect on the results obtained.
However, this result is simply a consequence of the scales on which the variables were measured. For instance, if Assault were measured in units of the number of occurrences per 100 people (rather than number of occurrences per 100, 000 people), then this would amount to dividing all of the elements of that variable by 1, 000. Then the variance of the variable would be tiny, and so the frst principal component loading vector would have a very small value for that variable. Because it is undesirable for the principal components obtained to depend on an arbitrary choice of scaling, we typically scale each variable to have standard deviation one before we perform PCA.
In certain settings, however, the variables may be measured in the same units. In this case, we might not wish to scale the variables to have standard deviation one before performing PCA. For instance, suppose that the variables in a given data set correspond to expression levels for p genes. Then since expression is measured in the same “units” for each gene, we might choose not to scale the genes to each have standard deviation one.
Uniqueness of the Principal Components
While in theory the principal components need not be unique, in almost all practical settings they are (up to sign fips). This means that two diferent software packages will yield the same principal component loading vectors, although the signs of those loading vectors may difer. The signs may difer because each principal component loading vector specifes a direction in pdimensional space: fipping the sign has no efect as the direction does not change. (Consider Figure 6.14—the principal component loading vector is a line that extends in either direction, and fipping its sign would have no efect.) Similarly, the score vectors are unique up to a sign fip, since the variance of Z is the same as the variance of −Z. It is worth noting that when we use (12.5) to approximate xij we multiply zim by φjm. Hence, if the sign is fipped on both the loading and score vectors, the fnal product of the two quantities is unchanged.
Deciding How Many Principal Components to Use
In general, an n × p data matrix X has min(n − 1, p) distinct principal components. However, we usually are not interested in all of them; rather, we would like to use just the frst few principal components in order to visualize or interpret the data. In fact, we would like to use the smallest number of principal components required to get a good understanding of the data. How many principal components are needed? Unfortunately, there is no single (or simple!) answer to this question.
We typically decide on the number of principal components required to visualize the data by examining a scree plot, such as the one shown in the left-hand panel of Figure 12.3. We choose the smallest number of principal components that are required in order to explain a sizable amount of the variation in the data. This is done by eyeballing the scree plot, and looking for a point at which the proportion of variance explained by each subsequent principal component drops of. This drop is often referred to as an elbow in the scree plot. For instance, by inspection of Figure 12.3, one might conclude that a fair amount of variance is explained by the frst two principal components, and that there is an elbow after the second component. After all, the third principal component explains less than ten percent of the variance in the data, and the fourth principal component explains less than half that and so is essentially worthless.
However, this type of visual analysis is inherently ad hoc. Unfortunately, there is no well-accepted objective way to decide how many principal components are enough. In fact, the question of how many principal components are enough is inherently ill-defned, and will depend on the specifc area of application and the specifc data set. In practice, we tend to look at the frst few principal components in order to fnd interesting patterns in the data. If no interesting patterns are found in the frst few principal components, then further principal components are unlikely to be of interest. Conversely, if the frst few principal components are interesting, then we typically continue to look at subsequent principal components until no further interesting patterns are found. This is admittedly a subjective approach, and is refective of the fact that PCA is generally used as a tool for exploratory data analysis.
On the other hand, if we compute principal components for use in a supervised analysis, such as the principal components regression presented in Section 6.3.1, then there is a simple and objective way to determine how many principal components to use: we can treat the number of principal component score vectors to be used in the regression as a tuning parameter to be selected via cross-validation or a related approach. The comparative simplicity of selecting the number of principal components for a supervised analysis is one manifestation of the fact that supervised analyses tend to be more clearly defned and more objectively evaluated than unsupervised analyses.
12.2.5 Other Uses for Principal Components
We saw in Section 6.3.1 that we can perform regression using the principal component score vectors as features. In fact, many statistical techniques, such as regression, classifcation, and clustering, can be easily adapted to use the n × M matrix whose columns are the frst M ≪ p principal component score vectors, rather than using the full n × p data matrix. This can lead to less noisy results, since it is often the case that the signal (as opposed to the noise) in a data set is concentrated in its frst few principal components.
12.3 Missing Values and Matrix Completion
Often datasets have missing values, which can be a nuisance. For example, suppose that we wish to analyze the USArrests data, and discover that 20 of the 200 values have been randomly corrupted and marked as missing. Unfortunately, the statistical learning methods that we have seen in this book cannot handle missing values. How should we proceed?
We could remove the rows that contain missing observations and perform our data analysis on the complete rows. But this seems wasteful, and depending on the fraction missing, unrealistic. Alternatively, if xij is missing, then we could replace it by the mean of the jth column (using the non-missing entries to compute the mean). Although this is a common and convenient strategy, often we can do better by exploiting the correlation between the variables.
In this section we show how principal components can be used to impute impute imputation the missing values, through a process known as matrix completion. The completed matrix can then be used in a statistical learning method, such as linear regression or LDA.
matrix completion
This approach for imputing missing data is appropriate if the missingness is random. For example, it is suitable if a patient’s weight is missing because missing at the battery of the electronic scale was fat at the time of his exam. By random contrast, if the weight is missing because the patient was too heavy to climb on the scale, then this is not missing at random; the missingness is
informative, and the approach described here for handling missing data is not suitable.
Sometimes data is missing by necessity. For example, if we form a matrix of the ratings (on a scale from 1 to 5) that n customers have given to the entire Netfix catalog of p movies, then most of the matrix will be missing, since no customer will have seen and rated more than a tiny fraction of the catalog. If we can impute the missing values well, then we will have an idea of what each customer will think of movies they have not yet seen. Hence matrix completion can be used to power recommender systems. recommender
systems
Principal Components with Missing Values
In Section 12.2.2, we showed that the frst M principal component score and loading vectors provide the “best” approximation to the data matrix X, in the sense of (12.6). Suppose that some of the observations xij are missing. We now show how one can both impute the missing values and solve the principal component problem at the same time. We return to a modifed form of the optimization problem (12.6),
\[\underset{\mathbf{A}\in\mathbb{R}^{n\times M},\mathbf{B}\in\mathbb{R}^{p\times M}}{\text{minimize}}\left\{\sum\_{(i,j)\in\mathcal{O}}\left(x\_{ij}-\sum\_{m=1}^{M}a\_{im}b\_{jm}\right)^{2}\right\},\tag{12.12}\]
where O is the set of all observed pairs of indices (i, j), a subset of the possible n × p pairs.
Once we solve this problem:
- we can estimate a missing observation xij using xˆij = #M m=1 aˆimˆbjm, where aˆim and ˆbjm are the (i, m) and (j, m) elements, respectively, of the matrices Aˆ and Bˆ that solve (12.12); and
- we can (approximately) recover the M principal component scores and loadings, as we did when the data were complete.
It turns out that solving (12.12) exactly is difcult, unlike in the case of complete data: the eigen decomposition no longer applies. But the simple iterative approach in Algorithm 12.1, which is demonstrated in Section 12.5.2, typically provides a good solution.56
We illustrate Algorithm 12.1 on the USArrests data. There are p = 4 variables and n = 50 observations (states). We frst standardized the data so each variable has mean zero and standard deviation one. We then randomly selected 20 of the 50 states, and then for each of these we randomly set one of the four variables to be missing. Thus, 10% of the elements of the data matrix were missing. We applied Algorithm 12.1 with M = 1 principal component. Figure 12.5 shows that the recovery of the missing elements
5This algorithm is referred to as “Hard-Impute” in Mazumder, Hastie, and Tibshirani (2010) “Spectral regularization algorithms for learning large incomplete matrices”, published in Journal of Machine Learning Research, pages 2287–2322.
6Each iteration of Step 2 of this algorithm decreases the objective (12.14). However, the algorithm is not guaranteed to achieve the global optimum of (12.12).
Algorithm 12.1 Iterative Algorithm for Matrix Completion
- Create a complete data matrix X˜ of dimension n × p of which the (i, j) element equals
\[ \tilde{x}\_{ij} = \begin{cases} \ x\_{ij} & \text{if } (i,j) \in \mathcal{O} \\ \ \bar{x}\_j & \text{if } (i,j) \notin \mathcal{O}, \end{cases} \]
where x¯j is the average of the observed values for the jth variable in the incomplete data matrix X. Here, O indexes the observations that are observed in X.
- Repeat steps (a)–(c) until the objective (12.14) fails to decrease:
- Solve
\[\underset{\mathbf{A}\in\mathbb{R}^{n\times M},\mathbf{B}\in\mathbb{R}^{p\times M}}{\text{minimize}}\left\{\sum\_{j=1}^{p}\sum\_{i=1}^{n}\left(\tilde{x}\_{ij}-\sum\_{m=1}^{M}a\_{im}b\_{jm}\right)^{2}\right\}\tag{12.13}\]
by computing the principal components of X˜ .
- For each element (i, j) ∈/ O, set x˜ij ← #M m=1 aˆimˆbjm.
- Compute the objective
\[\sum\_{(i,j)\in\mathcal{O}} \left( x\_{ij} - \sum\_{m=1}^{M} \hat{a}\_{im} \hat{b}\_{jm} \right)^2. \tag{12.14}\]
- Return the estimated missing entries x˜ij , (i, j) ∈/ O.
is pretty accurate. Over 100 random runs of this experiment, the average correlation between the true and imputed values of the missing elements is 0.63, with a standard deviation of 0.11. Is this good performance? To answer this question, we can compare this correlation to what we would have gotten if we had estimated these 20 values using the complete data — that is, if we had simply computed xˆij = zi1φj1, where zi1 and φj1 are elements of the frst principal component score and loading vectors of the complete data.7 Using the complete data in this way results in an average correlation of 0.79 between the true and estimated values for these 20 elements, with a standard deviation of 0.08. Thus, our imputation method does worse than the method that uses all of the data (0.63 ± 0.11 versus 0.79 ± 0.08), but its performance is still pretty good. (And of course, the method that uses all of the data cannot be applied in a real-world setting with missing data.)
Figure 12.6 further indicates that Algorithm 12.1 performs fairly well on this dataset.
7This is an unattainable gold standard, in the sense that with missing data, we of course cannot compute the principal components of the complete data.
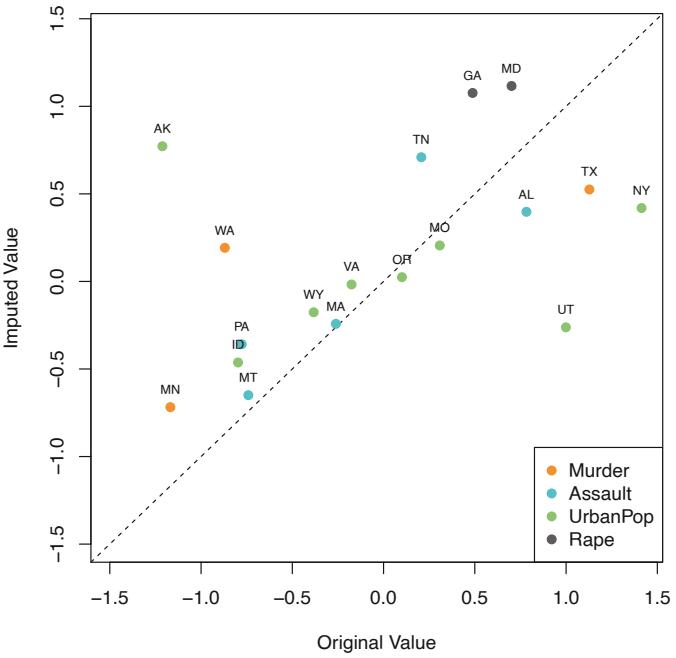
FIGURE 12.5. Missing value imputation on the USArrests data. Twenty values (10% of the total number of matrix elements) were artifcially set to be missing, and then imputed via Algorithm 12.1 with M = 1. The fgure displays the true value xij and the imputed value xˆij for all twenty missing values. For each of the twenty missing values, the color indicates the variable, and the label indicates the state. The correlation between the true and imputed values is around 0.63.
We close with a few observations:
- The USArrests data has only four variables, which is on the low end for methods like Algorithm 12.1 to work well. For this reason, for this demonstration we randomly set at most one variable per state to be missing, and only used M = 1 principal component.
- In general, in order to apply Algorithm 12.1, we must select M, the number of principal components to use for the imputation. One approach is to randomly leave out a few additional elements from the matrix, and select M based on how well those known values are recovered. This is closely related to the validation-set approach seen in Chapter 5.
Recommender Systems
Digital streaming services like Netfix and Amazon use data about the content that a customer has viewed in the past, as well as data from other customers, to suggest other content for the customer. As a concrete example, some years back, Netfix had customers rate each movie that they had seen with a score from 1–5. This resulted in a very big n × p matrix for which the (i, j) element is the rating given by the ith customer to the
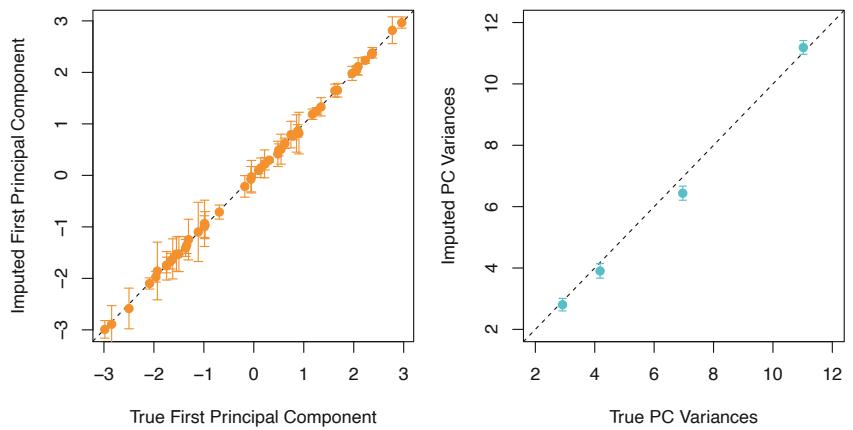
FIGURE 12.6. As described in the text, in each of 100 trials, we left out 20 elements of the USArrests dataset. In each trial, we applied Algorithm 12.1 with M = 1 to impute the missing elements and compute the principal components. Left: For each of the 50 states, the imputed frst principal component scores (averaged over 100 trials, and displayed with a standard deviation bar) are plotted against the frst principal component scores computed using all the data. Right: The imputed principal component loadings (averaged over 100 trials, and displayed with a standard deviation bar) are plotted against the true principal component loadings.
jth movie. One specifc early example of this matrix had n = 480,189 customers and p = 17,770 movies. However, on average each customer had seen around 200 movies, so 99% of the matrix had missing elements. Table 12.2 illustrates the setup.
In order to suggest a movie that a particular customer might like, Netfix needed a way to impute the missing values of this data matrix. The key idea is as follows: the set of movies that the ith customer has seen will overlap with those that other customers have seen. Furthermore, some of those other customers will have similar movie preferences to the ith customer. Thus, it should be possible to use similar customers’ ratings of movies that the ith customer has not seen to predict whether the ith customer will like those movies.
More concretely, by applying Algorithm 12.1, we can predict the ith customer’s rating for the jth movie using xˆij = #M m=1 aˆimˆbjm. Furthermore, we can interpret the M components in terms of “cliques” and “genres”:
- aˆim represents the strength with which the ith user belongs to the mth clique, where a clique is a group of customers that enjoys movies of the mth genre;
- ˆbjm represents the strength with which the jth movie belongs to the mth genre.
Examples of genres include Romance, Western, and Action.
Principal component models similar to Algorithm 12.1 are at the heart of many recommender systems. Although the data matrices involved are
TABLE 12.2. Excerpt of the Netfix movie rating data. The movies are rated from 1 (worst) to 5 (best). The symbol • represents a missing value: a movie that was not rated by the corresponding customer.
typically massive, algorithms have been developed that can exploit the high level of missingness in order to perform efcient computations.
12.4 Clustering Methods
Clustering refers to a very broad set of techniques for fnding subgroups, or clustering clusters, in a data set. When we cluster the observations of a data set, we seek to partition them into distinct groups so that the observations within each group are quite similar to each other, while observations in diferent groups are quite diferent from each other. Of course, to make this concrete, we must defne what it means for two or more observations to be similar or diferent. Indeed, this is often a domain-specifc consideration that must be made based on knowledge of the data being studied.
For instance, suppose that we have a set of n observations, each with p features. The n observations could correspond to tissue samples for patients with breast cancer, and the p features could correspond to measurements collected for each tissue sample; these could be clinical measurements, such as tumor stage or grade, or they could be gene expression measurements. We may have a reason to believe that there is some heterogeneity among the n tissue samples; for instance, perhaps there are a few diferent unknown subtypes of breast cancer. Clustering could be used to fnd these subgroups. This is an unsupervised problem because we are trying to discover structure—in this case, distinct clusters—on the basis of a data set. The goal in supervised problems, on the other hand, is to try to predict some outcome vector such as survival time or response to drug treatment.
Both clustering and PCA seek to simplify the data via a small number of summaries, but their mechanisms are diferent:
- PCA looks to fnd a low-dimensional representation of the observations that explain a good fraction of the variance;
- Clustering looks to fnd homogeneous subgroups among the observations.
Another application of clustering arises in marketing. We may have access to a large number of measurements (e.g. median household income, occupation, distance from nearest urban area, and so forth) for a large number of people. Our goal is to perform market segmentation by identifying subgroups of people who might be more receptive to a particular form of advertising, or more likely to purchase a particular product. The task of performing market segmentation amounts to clustering the people in the data set.
Since clustering is popular in many felds, there exist a great number of clustering methods. In this section we focus on perhaps the two best-known clustering approaches: K-means clustering and hierarchical K-means clustering clustering. In K-means clustering, we seek to partition the observations into a pre-specifed number of clusters. On the other hand, in hierarchical clustering, we do not know in advance how many clusters we want; in fact, we end up with a tree-like visual representation of the observations, called a dendrogram, that allows us to view at once the clusterings obtained for dendrogram each possible number of clusters, from 1 to n. There are advantages and disadvantages to each of these clustering approaches, which we highlight in this chapter.
hierarchical clustering
In general, we can cluster observations on the basis of the features in order to identify subgroups among the observations, or we can cluster features on the basis of the observations in order to discover subgroups among the features. In what follows, for simplicity we will discuss clustering observations on the basis of the features, though the converse can be performed by simply transposing the data matrix.
12.4.1 K-Means Clustering
K-means clustering is a simple and elegant approach for partitioning a data set into K distinct, non-overlapping clusters. To perform K-means clustering, we must frst specify the desired number of clusters K; then the K-means algorithm will assign each observation to exactly one of the K clusters. Figure 12.7 shows the results obtained from performing K-means clustering on a simulated example consisting of 150 observations in two dimensions, using three diferent values of K.
The K-means clustering procedure results from a simple and intuitive mathematical problem. We begin by defning some notation. Let C1,…,CK denote sets containing the indices of the observations in each cluster. These sets satisfy two properties:
- C1 ∪ C2 ∪ ··· ∪ CK = {1,…,n}. In other words, each observation belongs to at least one of the K clusters.
- Ck ∩ Ck′ = ∅ for all k ≠ k′ . In other words, the clusters are nonoverlapping: no observation belongs to more than one cluster.
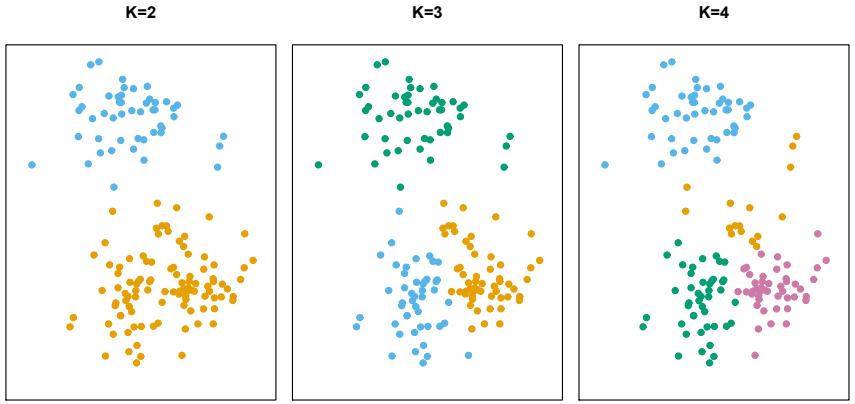
FIGURE 12.7. A simulated data set with 150 observations in two-dimensional space. Panels show the results of applying K-means clustering with diferent values of K, the number of clusters. The color of each observation indicates the cluster to which it was assigned using the K-means clustering algorithm. Note that there is no ordering of the clusters, so the cluster coloring is arbitrary. These cluster labels were not used in clustering; instead, they are the outputs of the clustering procedure.
For instance, if the ith observation is in the kth cluster, then i ∈ Ck. The idea behind K-means clustering is that a good clustering is one for which the within-cluster variation is as small as possible. The within-cluster variation for cluster Ck is a measure W(Ck) of the amount by which the observations within a cluster difer from each other. Hence we want to solve the problem
\[\underset{C\_1,\ldots,C\_K}{\text{minimize}} \left\{ \sum\_{k=1}^K W(C\_k) \right\}.\tag{12.15}\]
In words, this formula says that we want to partition the observations into K clusters such that the total within-cluster variation, summed over all K clusters, is as small as possible.
Solving (12.15) seems like a reasonable idea, but in order to make it actionable we need to defne the within-cluster variation. There are many possible ways to defne this concept, but by far the most common choice involves squared Euclidean distance. That is, we defne
\[W(C\_k) = \frac{1}{|C\_k|} \sum\_{i, i' \in C\_k} \sum\_{j=1}^p (x\_{ij} - x\_{i'j})^2,\tag{12.16}\]
where |Ck| denotes the number of observations in the kth cluster. In other words, the within-cluster variation for the kth cluster is the sum of all of the pairwise squared Euclidean distances between the observations in the kth cluster, divided by the total number of observations in the kth cluster. Combining (12.15) and (12.16) gives the optimization problem that defnes K-means clustering,
\[\underset{C\_{1},...,C\_{K}}{\text{minimize}} \left\{ \sum\_{k=1}^{K} \frac{1}{|C\_{k}|} \sum\_{i,i' \in C\_{k}} \sum\_{j=1}^{p} (x\_{ij} - x\_{i'j})^2 \right\}.\tag{12.17}\]
Now, we would like to fnd an algorithm to solve (12.17)—that is, a method to partition the observations into K clusters such that the objective of (12.17) is minimized. This is in fact a very difcult problem to solve precisely, since there are almost Kn ways to partition n observations into K clusters. This is a huge number unless K and n are tiny! Fortunately, a very simple algorithm can be shown to provide a local optimum—a pretty good solution—to the K-means optimization problem (12.17). This approach is laid out in Algorithm 12.2.
Algorithm 12.2 K-Means Clustering
- Randomly assign a number, from 1 to K, to each of the observations. These serve as initial cluster assignments for the observations.
- Iterate until the cluster assignments stop changing:
- For each of the K clusters, compute the cluster centroid. The kth cluster centroid is the vector of the p feature means for the observations in the kth cluster.
- Assign each observation to the cluster whose centroid is closest (where closest is defned using Euclidean distance).
Algorithm 12.2 is guaranteed to decrease the value of the objective (12.17) at each step. To understand why, the following identity is illuminating:
\[\frac{1}{|C\_k|} \sum\_{i, i' \in C\_k} \sum\_{j=1}^p (x\_{ij} - x\_{i'j})^2 = 2 \sum\_{i \in C\_k} \sum\_{j=1}^p (x\_{ij} - \bar{x}\_{kj})^2,\tag{12.18}\]
where x¯kj = 1 |Ck| # i∈Ck xij is the mean for feature j in cluster Ck. In Step 2(a) the cluster means for each feature are the constants that minimize the sum-of-squared deviations, and in Step 2(b), reallocating the observations can only improve (12.18). This means that as the algorithm is run, the clustering obtained will continually improve until the result no longer changes; the objective of (12.17) will never increase. When the result no longer changes, a local optimum has been reached. Figure 12.8 shows the progression of the algorithm on the toy example from Figure 12.7. K-means clustering derives its name from the fact that in Step 2(a), the cluster centroids are computed as the mean of the observations assigned to each cluster.
Because the K-means algorithm fnds a local rather than a global optimum, the results obtained will depend on the initial (random) cluster assignment of each observation in Step 1 of Algorithm 12.2. For this reason, it is important to run the algorithm multiple times from diferent random
FIGURE 12.8. The progress of the K-means algorithm on the example of Figure 12.7 with K=3. Top left: the observations are shown. Top center: in Step 1 of the algorithm, each observation is randomly assigned to a cluster. Top right: in Step 2(a), the cluster centroids are computed. These are shown as large colored disks. Initially the centroids are almost completely overlapping because the initial cluster assignments were chosen at random. Bottom left: in Step 2(b), each observation is assigned to the nearest centroid. Bottom center: Step 2(a) is once again performed, leading to new cluster centroids. Bottom right: the results obtained after ten iterations.
initial confgurations. Then one selects the best solution, i.e. that for which the objective (12.17) is smallest. Figure 12.9 shows the local optima obtained by running K-means clustering six times using six diferent initial cluster assignments, using the toy data from Figure 12.7. In this case, the best clustering is the one with an objective value of 235.8.
As we have seen, to perform K-means clustering, we must decide how many clusters we expect in the data. The problem of selecting K is far from simple. This issue, along with other practical considerations that arise in performing K-means clustering, is addressed in Section 12.4.3.
FIGURE 12.9. K-means clustering performed six times on the data from Figure 12.7 with K = 3, each time with a diferent random assignment of the observations in Step 1 of the K-means algorithm. Above each plot is the value of the objective (12.17). Three diferent local optima were obtained, one of which resulted in a smaller value of the objective and provides better separation between the clusters. Those labeled in red all achieved the same best solution, with an objective value of 235.8.
12.4.2 Hierarchical Clustering
One potential disadvantage of K-means clustering is that it requires us to pre-specify the number of clusters K. Hierarchical clustering is an alternative approach which does not require that we commit to a particular choice of K. Hierarchical clustering has an added advantage over K-means clustering in that it results in an attractive tree-based representation of the observations, called a dendrogram.
In this section, we describe bottom-up or agglomerative clustering. bottom-up agglomerative This is the most common type of hierarchical clustering, and refers to the fact that a dendrogram (generally depicted as an upside-down tree; see Figure 12.11) is built starting from the leaves and combining clusters up to the trunk. We will begin with a discussion of how to interpret a dendrogram
FIGURE 12.10. Forty-fve observations generated in two-dimensional space. In reality there are three distinct classes, shown in separate colors. However, we will treat these class labels as unknown and will seek to cluster the observations in order to discover the classes from the data.
and then discuss how hierarchical clustering is actually performed—that is, how the dendrogram is built.
Interpreting a Dendrogram
We begin with the simulated data set shown in Figure 12.10, consisting of 45 observations in two-dimensional space. The data were generated from a three-class model; the true class labels for each observation are shown in distinct colors. However, suppose that the data were observed without the class labels, and that we wanted to perform hierarchical clustering of the data. Hierarchical clustering (with complete linkage, to be discussed later) yields the result shown in the left-hand panel of Figure 12.11. How can we interpret this dendrogram?
In the left-hand panel of Figure 12.11, each leaf of the dendrogram represents one of the 45 observations in Figure 12.10. However, as we move up the tree, some leaves begin to fuse into branches. These correspond to observations that are similar to each other. As we move higher up the tree, branches themselves fuse, either with leaves or other branches. The earlier (lower in the tree) fusions occur, the more similar the groups of observations are to each other. On the other hand, observations that fuse later (near the top of the tree) can be quite diferent. In fact, this statement can be made precise: for any two observations, we can look for the point in the tree where branches containing those two observations are frst fused. The height of this fusion, as measured on the vertical axis, indicates how diferent the two observations are. Thus, observations that fuse at the very bottom of the tree are quite similar to each other, whereas observations that fuse close to the top of the tree will tend to be quite diferent.
This highlights a very important point in interpreting dendrograms that is often misunderstood. Consider the left-hand panel of Figure 12.12, which shows a simple dendrogram obtained from hierarchically clustering nine
FIGURE 12.11. Left: dendrogram obtained from hierarchically clustering the data from Figure 12.10 with complete linkage and Euclidean distance. Center: the dendrogram from the left-hand panel, cut at a height of nine (indicated by the dashed line). This cut results in two distinct clusters, shown in diferent colors. Right: the dendrogram from the left-hand panel, now cut at a height of fve. This cut results in three distinct clusters, shown in diferent colors. Note that the colors were not used in clustering, but are simply used for display purposes in this fgure.
observations. One can see that observations 5 and 7 are quite similar to each other, since they fuse at the lowest point on the dendrogram. Observations 1 and 6 are also quite similar to each other. However, it is tempting but incorrect to conclude from the fgure that observations 9 and 2 are quite similar to each other on the basis that they are located near each other on the dendrogram. In fact, based on the information contained in the dendrogram, observation 9 is no more similar to observation 2 than it is to observations 8, 5, and 7. (This can be seen from the right-hand panel of Figure 12.12, in which the raw data are displayed.) To put it mathematically, there are 2n−1 possible reorderings of the dendrogram, where n is the number of leaves. This is because at each of the n − 1 points where fusions occur, the positions of the two fused branches could be swapped without afecting the meaning of the dendrogram. Therefore, we cannot draw conclusions about the similarity of two observations based on their proximity along the horizontal axis. Rather, we draw conclusions about the similarity of two observations based on the location on the vertical axis where branches containing those two observations frst are fused.
Now that we understand how to interpret the left-hand panel of Figure 12.11, we can move on to the issue of identifying clusters on the basis of a dendrogram. In order to do this, we make a horizontal cut across the dendrogram, as shown in the center and right-hand panels of Figure 12.11. The distinct sets of observations beneath the cut can be interpreted as clusters. In the center panel of Figure 12.11, cutting the dendrogram at a height of nine results in two clusters, shown in distinct colors. In the right-hand panel, cutting the dendrogram at a height of fve results in three clusters. Further cuts can be made as one descends the dendrogram in order to obtain any number of clusters, between 1 (corresponding to no cut) and n
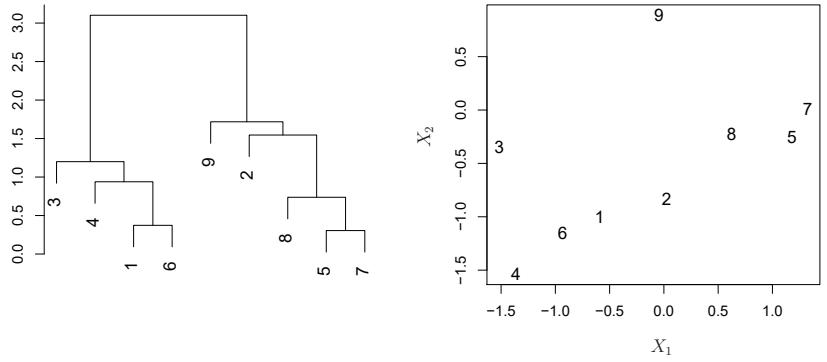
FIGURE 12.12. An illustration of how to properly interpret a dendrogram with nine observations in two-dimensional space. Left: a dendrogram generated using Euclidean distance and complete linkage. Observations 5 and 7 are quite similar to each other, as are observations 1 and 6. However, observation 9 is no more similar to observation 2 than it is to observations 8, 5, and 7, even though observations 9 and 2 are close together in terms of horizontal distance. This is because observations 2, 8, 5, and 7 all fuse with observation 9 at the same height, approximately 1.8. Right: the raw data used to generate the dendrogram can be used to confrm that indeed, observation 9 is no more similar to observation 2 than it is to observations 8, 5, and 7.
(corresponding to a cut at height 0, so that each observation is in its own cluster). In other words, the height of the cut to the dendrogram serves the same role as the K in K-means clustering: it controls the number of clusters obtained.
Figure 12.11 therefore highlights a very attractive aspect of hierarchical clustering: one single dendrogram can be used to obtain any number of clusters. In practice, people often look at the dendrogram and select by eye a sensible number of clusters, based on the heights of the fusion and the number of clusters desired. In the case of Figure 12.11, one might choose to select either two or three clusters. However, often the choice of where to cut the dendrogram is not so clear.
The term hierarchical refers to the fact that clusters obtained by cutting the dendrogram at a given height are necessarily nested within the clusters obtained by cutting the dendrogram at any greater height. However, on an arbitrary data set, this assumption of hierarchical structure might be unrealistic. For instance, suppose that our observations correspond to a group of men and women, evenly split among Americans, Japanese, and French. We can imagine a scenario in which the best division into two groups might split these people by gender, and the best division into three groups might split them by nationality. In this case, the true clusters are not nested, in the sense that the best division into three groups does not result from taking the best division into two groups and splitting up one of those groups. Consequently, this situation could not be well-represented by hierarchical clustering. Due to situations such as this one, hierarchical clustering can sometimes yield worse (i.e. less accurate) results than Kmeans clustering for a given number of clusters.
Algorithm 12.3 Hierarchical Clustering
- Begin with n observations and a measure (such as Euclidean distance) of all the 5n 2 6 = n(n − 1)/2 pairwise dissimilarities. Treat each observation as its own cluster.
- For i = n, n − 1,…, 2:
- Examine all pairwise inter-cluster dissimilarities among the i clusters and identify the pair of clusters that are least dissimilar (that is, most similar). Fuse these two clusters. The dissimilarity between these two clusters indicates the height in the dendrogram at which the fusion should be placed.
- Compute the new pairwise inter-cluster dissimilarities among the i − 1 remaining clusters.
The Hierarchical Clustering Algorithm
The hierarchical clustering dendrogram is obtained via an extremely simple algorithm. We begin by defning some sort of dissimilarity measure between each pair of observations. Most often, Euclidean distance is used; we will discuss the choice of dissimilarity measure later in this chapter. The algorithm proceeds iteratively. Starting out at the bottom of the dendrogram, each of the n observations is treated as its own cluster. The two clusters that are most similar to each other are then fused so that there now are n−1 clusters. Next the two clusters that are most similar to each other are fused again, so that there now are n − 2 clusters. The algorithm proceeds in this fashion until all of the observations belong to one single cluster, and the dendrogram is complete. Figure 12.13 depicts the frst few steps of the algorithm, for the data from Figure 12.12. To summarize, the hierarchical clustering algorithm is given in Algorithm 12.3.
This algorithm seems simple enough, but one issue has not been addressed. Consider the bottom right panel in Figure 12.13. How did we determine that the cluster {5, 7} should be fused with the cluster {8}? We have a concept of the dissimilarity between pairs of observations, but how do we defne the dissimilarity between two clusters if one or both of the clusters contains multiple observations? The concept of dissimilarity between a pair of observations needs to be extended to a pair of groups of observations. This extension is achieved by developing the notion of linkage, which defnes the dissimilarity between two groups of observa- linkage tions. The four most common types of linkage—complete, average, single, and centroid—are briefy described in Table 12.3. Average, complete, and single linkage are most popular among statisticians. Average and complete linkage are generally preferred over single linkage, as they tend to yield more balanced dendrograms. Centroid linkage is often used in genomics, but sufers from a major drawback in that an inversion can occur, whereby inversion two clusters are fused at a height below either of the individual clusters in the dendrogram. This can lead to difculties in visualization as well as in interpretation of the dendrogram. The dissimilarities computed in Step 2(b)
| Linkage | Description | ||
|---|---|---|---|
| Complete | Maximal intercluster dissimilarity. Compute all pairwise dissimilarities between the observations in cluster A and the observations in cluster B, and record the largest of these dis similarities. |
||
| Single | Minimal intercluster dissimilarity. Compute all pairwise dis similarities between the observations in cluster A and the observations in cluster B, and record the smallest of these dissimilarities. Single linkage can result in extended, trailing clusters in which single observations are fused one-at-a-time. |
||
| Average | Mean intercluster dissimilarity. Compute all pairwise dis similarities between the observations in cluster A and the observations in cluster B, and record the average of these dissimilarities. |
||
| Centroid | Dissimilarity between the centroid for cluster A (a mean vector of length p) and the centroid for cluster B. Centroid linkage can result in undesirable inversions. |
TABLE 12.3. A summary of the four most commonly-used types of linkage in hierarchical clustering.
of the hierarchical clustering algorithm will depend on the type of linkage used, as well as on the choice of dissimilarity measure. Hence, the resulting dendrogram typically depends quite strongly on the type of linkage used, as is shown in Figure 12.14.
Choice of Dissimilarity Measure
Thus far, the examples in this chapter have used Euclidean distance as the dissimilarity measure. But sometimes other dissimilarity measures might be preferred. For example, correlation-based distance considers two observations to be similar if their features are highly correlated, even though the observed values may be far apart in terms of Euclidean distance. This is an unusual use of correlation, which is normally computed between variables; here it is computed between the observation profles for each pair of observations. Figure 12.15 illustrates the diference between Euclidean and correlation-based distance. Correlation-based distance focuses on the shapes of observation profles rather than their magnitudes.
The choice of dissimilarity measure is very important, as it has a strong efect on the resulting dendrogram. In general, careful attention should be paid to the type of data being clustered and the scientifc question at hand. These considerations should determine what type of dissimilarity measure is used for hierarchical clustering.
For instance, consider an online retailer interested in clustering shoppers based on their past shopping histories. The goal is to identify subgroups of similar shoppers, so that shoppers within each subgroup can be shown items and advertisements that are particularly likely to interest them. Suppose the data takes the form of a matrix where the rows are the shoppers and the columns are the items available for purchase; the elements of the data matrix indicate the number of times a given shopper has purchased a
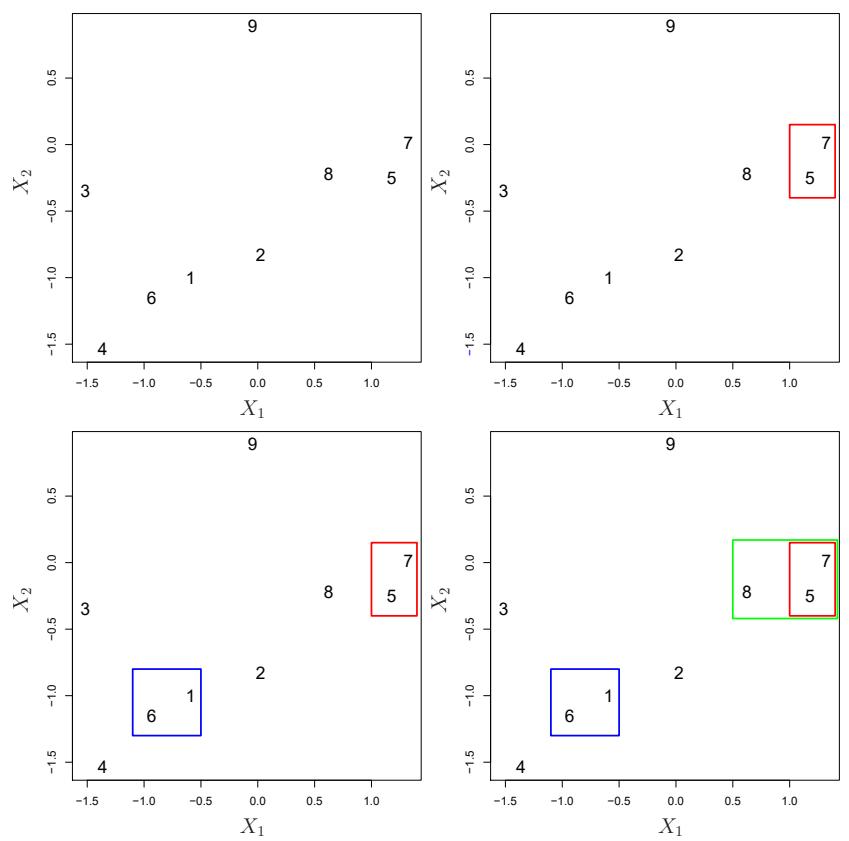
FIGURE 12.13. An illustration of the frst few steps of the hierarchical clustering algorithm, using the data from Figure 12.12, with complete linkage and Euclidean distance. Top Left: initially, there are nine distinct clusters, {1}, {2},…, {9}. Top Right: the two clusters that are closest together, {5} and {7}, are fused into a single cluster. Bottom Left: the two clusters that are closest together, {6} and {1}, are fused into a single cluster. Bottom Right: the two clusters that are closest together using complete linkage, {8} and the cluster {5, 7}, are fused into a single cluster.
given item (i.e. a 0 if the shopper has never purchased this item, a 1 if the shopper has purchased it once, etc.) What type of dissimilarity measure should be used to cluster the shoppers? If Euclidean distance is used, then shoppers who have bought very few items overall (i.e. infrequent users of the online shopping site) will be clustered together. This may not be desirable. On the other hand, if correlation-based distance is used, then shoppers with similar preferences (e.g. shoppers who have bought items A and B but never items C or D) will be clustered together, even if some shoppers with these preferences are higher-volume shoppers than others. Therefore, for this application, correlation-based distance may be a better choice.
In addition to carefully selecting the dissimilarity measure used, one must also consider whether or not the variables should be scaled to have standard deviation one before the dissimilarity between the observations is computed. To illustrate this point, we continue with the online shopping ex-
FIGURE 12.14. Average, complete, and single linkage applied to an example data set. Average and complete linkage tend to yield more balanced clusters.
ample just described. Some items may be purchased more frequently than others; for instance, a shopper might buy ten pairs of socks a year, but a computer very rarely. High-frequency purchases like socks therefore tend to have a much larger efect on the inter-shopper dissimilarities, and hence on the clustering ultimately obtained, than rare purchases like computers. This may not be desirable. If the variables are scaled to have standard deviation one before the inter-observation dissimilarities are computed, then each variable will in efect be given equal importance in the hierarchical clustering performed. We might also want to scale the variables to have standard deviation one if they are measured on diferent scales; otherwise, the choice of units (e.g. centimeters versus kilometers) for a particular variable will greatly afect the dissimilarity measure obtained. It should come as no surprise that whether or not it is a good decision to scale the variables before computing the dissimilarity measure depends on the application at hand. An example is shown in Figure 12.16. We note that the issue of whether or not to scale the variables before performing clustering applies to K-means clustering as well.
12.4.3 Practical Issues in Clustering
Clustering can be a very useful tool for data analysis in the unsupervised setting. However, there are a number of issues that arise in performing clustering. We describe some of these issues here.
Small Decisions with Big Consequences
In order to perform clustering, some decisions must be made.
FIGURE 12.15. Three observations with measurements on 20 variables are shown. Observations 1 and 3 have similar values for each variable and so there is a small Euclidean distance between them. But they are very weakly correlated, so they have a large correlation-based distance. On the other hand, observations 1 and 2 have quite diferent values for each variable, and so there is a large Euclidean distance between them. But they are highly correlated, so there is a small correlation-based distance between them.
- Should the observations or features frst be standardized in some way? For instance, maybe the variables should be scaled to have standard deviation one.
- In the case of hierarchical clustering,
- – What dissimilarity measure should be used?
- – What type of linkage should be used?
- – Where should we cut the dendrogram in order to obtain clusters?
- In the case of K-means clustering, how many clusters should we look for in the data?
Each of these decisions can have a strong impact on the results obtained. In practice, we try several diferent choices, and look for the one with the most useful or interpretable solution. With these methods, there is no single right answer—any solution that exposes some interesting aspects of the data should be considered.
Validating the Clusters Obtained
Any time clustering is performed on a data set we will fnd clusters. But we really want to know whether the clusters that have been found represent true subgroups in the data, or whether they are simply a result of clustering the noise. For instance, if we were to obtain an independent set of observations, then would those observations also display the same set of clusters? This is a hard question to answer. There exist a number of techniques for assigning a p-value to a cluster in order to assess whether there is more
FIGURE 12.16. An eclectic online retailer sells two items: socks and computers. Left: the number of pairs of socks, and computers, purchased by eight online shoppers is displayed. Each shopper is shown in a diferent color. If inter-observation dissimilarities are computed using Euclidean distance on the raw variables, then the number of socks purchased by an individual will drive the dissimilarities obtained, and the number of computers purchased will have little efect. This might be undesirable, since (1) computers are more expensive than socks and so the online retailer may be more interested in encouraging shoppers to buy computers than socks, and (2) a large diference in the number of socks purchased by two shoppers may be less informative about the shoppers’ overall shopping preferences than a small diference in the number of computers purchased. Center: the same data are shown, after scaling each variable by its standard deviation. Now the two products will have a comparable efect on the inter-observation dissimilarities obtained. Right: the same data are displayed, but now the y-axis represents the number of dollars spent by each online shopper on socks and on computers. Since computers are much more expensive than socks, now computer purchase history will drive the inter-observation dissimilarities obtained.
evidence for the cluster than one would expect due to chance. However, there has been no consensus on a single best approach. More details can be found in ESL.8
Other Considerations in Clustering
Both K-means and hierarchical clustering will assign each observation to a cluster. However, sometimes this might not be appropriate. For instance, suppose that most of the observations truly belong to a small number of (unknown) subgroups, and a small subset of the observations are quite diferent from each other and from all other observations. Then since Kmeans and hierarchical clustering force every observation into a cluster, the clusters found may be heavily distorted due to the presence of outliers that do not belong to any cluster. Mixture models are an attractive approach for accommodating the presence of such outliers. These amount to a soft version of K-means clustering, and are described in ESL.
8ESL: The Elements of Statistical Learning by Hastie, Tibshirani and Friedman.
In addition, clustering methods generally are not very robust to perturbations to the data. For instance, suppose that we cluster n observations, and then cluster the observations again after removing a subset of the n observations at random. One would hope that the two sets of clusters obtained would be quite similar, but often this is not the case!
A Tempered Approach to Interpreting the Results of Clustering
We have described some of the issues associated with clustering. However, clustering can be a very useful and valid statistical tool if used properly. We mentioned that small decisions in how clustering is performed, such as how the data are standardized and what type of linkage is used, can have a large efect on the results. Therefore, we recommend performing clustering with diferent choices of these parameters, and looking at the full set of results in order to see what patterns consistently emerge. Since clustering can be non-robust, we recommend clustering subsets of the data in order to get a sense of the robustness of the clusters obtained. Most importantly, we must be careful about how the results of a clustering analysis are reported. These results should not be taken as the absolute truth about a data set. Rather, they should constitute a starting point for the development of a scientifc hypothesis and further study, preferably on an independent data set.
12.5 Lab: Unsupervised Learning
In this lab we demonstrate PCA and clustering on several datasets. As in other labs, we import some of our libraries at this top level. This makes the code more readable, as scanning the frst few lines of the notebook tell us what libraries are used in this notebook.
In [1]: import numpy as npimport pandas as pd
import matplotlib.pyplot as plt
from statsmodels.datasets import get_rdataset
from sklearn.decomposition import PCA
from sklearn.preprocessing import StandardScaler
from ISLP import load_dataWe also collect the new imports needed for this lab.
In [2]: from sklearn.cluster import \
(KMeans,
AgglomerativeClustering)
from scipy.cluster.hierarchy import \
(dendrogram,
cut_tree)
from ISLP.cluster import compute_linkage12.5.1 Principal Components Analysis
In this lab, we perform PCA on USArrests, a data set in the R computing environment. We retrieve the data using get_rdataset(), which can fetch get_
rdataset()
536 12. Unsupervised Learning
data from many standard R packages.
The rows of the data set contain the 50 states, in alphabetical order.
In [3]: USArrests = get_rdataset('USArrests').data
USArrests
Out[3]: Murder Assault UrbanPop Rape
Alabama 13.2 236 58 21.2
Alaska 10.0 263 48 44.5
Arizona 8.1 294 80 31.0
... ... ... ... ...
Wisconsin 2.6 53 66 10.8
Wyoming 6.8 161 60 15.6The columns of the data set contain the four variables.
In [4]: USArrests.columnsOut[4]: Index(['Murder', 'Assault', 'UrbanPop', 'Rape'],
dtype='object')We frst briefy examine the data. We notice that the variables have vastly diferent means.
In [5]: USArrests.mean()Out[5]: Murder 7.788
Assault 170.760
UrbanPop 65.540
Rape 21.232
dtype: float64Dataframes have several useful methods for computing column-wise summaries. We can also examine the variance of the four variables using the var() method.
In [6]: USArrests.var()Out[6]: Murder 18.970465
Assault 6945.165714
UrbanPop 209.518776
Rape 87.729159
dtype: float64Not surprisingly, the variables also have vastly diferent variances. The UrbanPop variable measures the percentage of the population in each state living in an urban area, which is not a comparable number to the number of rapes in each state per 100,000 individuals. PCA looks for derived variables that account for most of the variance in the data set. If we do not scale the variables before performing PCA, then the principal components would mostly be driven by the Assault variable, since it has by far the largest variance. So if the variables are measured in diferent units or vary widely in scale, it is recommended to standardize the variables to have standard deviation one before performing PCA. Typically we set the means to zero as well.
This scaling can be done via the StandardScaler() transform imported above. We frst fit the scaler, which computes the necessary means and standard deviations and then apply it to our data using the transform method. As before, we combine these steps using the fit_transform() method.
In [7]: scaler = StandardScaler(with_std=True,
with_mean=True)
USArrests_scaled = scaler.fit_transform(USArrests)Having scaled the data, we can then perform principal components analysis using the PCA() transform from the sklearn.decomposition package. PCA()
In [8]: pcaUS = PCA()
(By default, the PCA() transform centers the variables to have mean zero though it does not scale them.) The transform pcaUS can be used to fnd the PCA scores returned by fit(). Once the fit method has been called, the pcaUS object also contains a number of useful quantities.
In [9]: pcaUS.fit(USArrests_scaled)After ftting, the mean_ attribute corresponds to the means of the variables. In this case, since we centered and scaled the data with scaler() the means will all be 0.
In [10]: pcaUS.mean_Out[10]: array([-0., 0., -0., 0.])The scores can be computed using the transform() method of pcaUS after it has been ft.
In [11]: scores = pcaUS.transform(USArrests_scaled)We will plot these scores a bit further down. The components_ attribute provides the principal component loadings: each row of pcaUS.components_ contains the corresponding principal component loading vector.
In [12]: pcaUS.components_Out[12]: array([[ 0.53589947, 0.58318363, 0.27819087, 0.54343209],
[ 0.41818087, 0.1879856 , -0.87280619, -0.16731864],
[-0.34123273, -0.26814843, -0.37801579, 0.81777791],
[ 0.6492278 , -0.74340748, 0.13387773, 0.08902432]])The biplot is a common visualization method used with PCA. It is not built in as a standard part of sklearn, though there are python packages that do produce such plots. Here we make a simple biplot manually.
In [13]: i, j = 0, 1 # which components
fig, ax = plt.subplots(1, 1, figsize=(8, 8))
ax.scatter(scores[:,0], scores[:,1])
ax.set_xlabel('PC%d' % (i+1))
ax.set_ylabel('PC%d' % (j+1))
for k in range(pcaUS.components_.shape[1]):538 12. Unsupervised Learning
ax.arrow(0, 0, pcaUS.components_[i,k], pcaUS.components_[j,k])
ax.text(pcaUS.components_[i,k],
pcaUS.components_[j,k],
USArrests.columns[k])Notice that this fgure is a refection of Figure 12.1 through the y-axis. Recall that the principal components are only unique up to a sign change, so we can reproduce that fgure by fipping the signs of the second set of scores and loadings. We also increase the length of the arrows to emphasize the loadings.
In [14]: scale_arrow = s_ = 2
scores[:,1] *= -1
pcaUS.components_[1] *= -1 # flip the y-axis
fig, ax = plt.subplots(1, 1, figsize=(8, 8))
ax.scatter(scores[:,0], scores[:,1])
ax.set_xlabel('PC%d' % (i+1))
ax.set_ylabel('PC%d' % (j+1))
for k in range(pcaUS.components_.shape[1]):
ax.arrow(0, 0, s_*pcaUS.components_[i,k], s_*pcaUS.components_[
j,k])
ax.text(s_*pcaUS.components_[i,k],
s_*pcaUS.components_[j,k],
USArrests.columns[k])The standard deviations of the principal component scores are as follows:
In [15]: scores.std(0, ddof=1)Out[15]: array([1.5909, 1.0050, 0.6032, 0.4207])The variance of each score can be extracted directly from the pcaUS object via the explained_variance_ attribute.
In [16]: pcaUS.explained_variance_Out[16]: array([2.5309, 1.01 , 0.3638, 0.177 ])The proportion of variance explained by each principal component (PVE) is stored as explained_variance_ratio_:
In [17]: pcaUS.explained_variance_ratio_Out[17]: array([0.6201, 0.2474, 0.0891, 0.0434])We see that the frst principal component explains 62.0% of the variance in the data, the next principal component explains 24.7% of the variance, and so forth. We can plot the PVE explained by each component, as well as the cumulative PVE. We frst plot the proportion of variance explained.
In [18]: %%capture
fig, axes = plt.subplots(1, 2, figsize=(15, 6))
ticks = np.arange(pcaUS.n_components_)+1
ax = axes[0]
ax.plot(ticks,
pcaUS.explained_variance_ratio_,
marker='o')ax.set_xlabel('Principal Component');
ax.set_ylabel('Proportion of Variance Explained')
ax.set_ylim([0,1])
ax.set_xticks(ticks)Notice the use of %%capture, which suppresses the displaying of the partially completed fgure.
In [19]: ax = axes[1]
ax.plot(ticks,
pcaUS.explained_variance_ratio_.cumsum(),
marker='o')
ax.set_xlabel('Principal Component')
ax.set_ylabel('Cumulative Proportion of Variance Explained')
ax.set_ylim([0, 1])
ax.set_xticks(ticks)
figThe result is similar to that shown in Figure 12.3. Note that the method cumsum() computes the cumulative sum of the elements of a numeric vector. cumsum() For instance:
In [20]: a = np.array([1,2,8,-3]) np.cumsum(a)
Out[20]: array([ 1, 3, 11, 8])Out[21]: ((50, 4), (4,), (4, 4))
12.5.2 Matrix Completion
We now re-create the analysis carried out on the USArrests data in Section 12.3.
We saw in Section 12.2.2 that solving the optimization problem (12.6) on a centered data matrix X is equivalent to computing the frst M principal components of the data. We use our scaled and centered USArrests data as X below. The singular value decomposition (SVD) is a general algorithm singular for solving (12.6).
value decomposition svd()
In [21]: X = USArrests_scaled
U, D, V = np.linalg.svd(X, full_matrices=False)
U.shape, D.shape, V.shapeThe np.linalg.svd() function returns three components, U, D and V. The np.linalg. matrix svd() V is equivalent to the loading matrix from principal components (up
to an unimportant sign fip). Using the full_matrices=False option ensures
that for a tall matrix the shape of U is the same as the shape of X.
In [22]: VOut[22]: array([[-0.53589947, -0.58318363, -0.27819087, -0.54343209],
[ 0.41818087, 0.1879856 , -0.87280619, -0.16731864],
[-0.34123273, -0.26814843, -0.37801579, 0.81777791],
[ 0.6492278 , -0.74340748, 0.13387773, 0.08902432]])540 12. Unsupervised Learning
In [23]: pcaUS.components_
Out[23]: array([[ 0.53589947, 0.58318363, 0.27819087, 0.54343209],
[ 0.41818087, 0.1879856 , -0.87280619, -0.16731864],
[-0.34123273, -0.26814843, -0.37801579, 0.81777791],The matrix U corresponds to a standardized version of the PCA score matrix (each column standardized to have sum-of-squares one). If we multiply each column of U by the corresponding element of D, we recover the PCA scores exactly (up to a meaningless sign fip).
[ 0.6492278 , -0.74340748, 0.13387773, 0.08902432]])
In [24]: (U * D[None,:])[:3]Out[24]: array([[-0.9856, 1.1334, -0.4443, 0.1563],
[-1.9501, 1.0732, 2.04 , -0.4386],
[-1.7632, -0.746 , 0.0548, -0.8347]])In [25]: scores[:3]Out[25]: array([[ 0.9856, -1.1334, -0.4443, 0.1563],
[ 1.9501, -1.0732, 2.04 , -0.4386],
[ 1.7632, 0.746 , 0.0548, -0.8347]])While it would be possible to carry out this lab using the PCA() estimator, here we use the np.linalg.svd() function in order to illustrate its use.
We now omit 20 entries in the 50 × 4 data matrix at random. We do so by frst selecting 20 rows (states) at random, and then selecting one of the four entries in each row at random. This ensures that every row has at least three observed values.
In [26]: n_omit = 20
np.random.seed(15)
r_idx = np.random.choice(np.arange(X.shape[0]),
n_omit,
replace=False)
c_idx = np.random.choice(np.arange(X.shape[1]),
n_omit,
replace=True)
Xna = X.copy()
Xna[r_idx, c_idx] = np.nanHere the array r_idx contains 20 integers from 0 to 49; this represents the states (rows of X) that are selected to contain missing values. And c_idx contains 20 integers from 0 to 3, representing the features (columns in X) that contain the missing values for each of the selected states.
We now write some code to implement Algorithm 12.1. We frst write a function that takes in a matrix, and returns an approximation to the matrix using the svd() function. This will be needed in Step 2 of Algorithm 12.1.
In [27]: def low_rank(X, M=1):
U, D, V = np.linalg.svd(X)
L = U[:,:M] * D[None,:M]
return L.dot(V[:M])To conduct Step 1 of the algorithm, we initialize Xhat — this is X˜ in Algorithm 12.1 — by replacing the missing values with the column means of the non-missing entries. These are stored in Xbar below after running np.nanmean() over the row axis. We make a copy so that when we assign np.nanmean() values to Xhat below we do not also overwrite the values in Xna.
In [28]: Xhat = Xna.copy()
Xbar = np.nanmean(Xhat, axis=0)
Xhat[r_idx, c_idx] = Xbar[c_idx]Before we begin Step 2, we set ourselves up to measure the progress of our iterations:
In [29]: thresh = 1e-7
rel_err = 1
count = 0
ismiss = np.isnan(Xna)
mssold = np.mean(Xhat[∼ismiss]**2)
mss0 = np.mean(Xna[∼ismiss]**2)Here ismiss is a logical matrix with the same dimensions as Xna; a given element is True if the corresponding matrix element is missing. The notation ∼ismiss negates this boolean vector. This is useful because it allows us to access both the missing and non-missing entries. We store the mean of the squared non-missing elements in mss0. We store the mean squared error of the non-missing elements of the old version of Xhat in mssold (which currently agrees with mss0). We plan to store the mean squared error of the non-missing elements of the current version of Xhat in mss, and will then iterate Step 2 of Algorithm 12.1 until the relative error, defned as (mssold - mss) / mss0, falls below thresh = 1e-7. 9
In Step 2(a) of Algorithm 12.1, we approximate Xhat using low_rank(); we call this Xapp. In Step 2(b), we use Xapp to update the estimates for elements in Xhat that are missing in Xna. Finally, in Step 2(c), we compute the relative error. These three steps are contained in the following while loop:
In [30]: while rel_err > thresh:
count += 1
# Step 2(a)
Xapp = low_rank(Xhat, M=1)
# Step 2(b)
Xhat[ismiss] = Xapp[ismiss]
# Step 2(c)
mss = np.mean(((Xna - Xapp)[∼ismiss])**2)
rel_err = (mssold - mss) / mss0
mssold = mss
print("Iteration: {0}, MSS:{1:.3f}, Rel.Err {2:.2e}"
.format(count, mss, rel_err))9Algorithm 12.1 tells us to iterate Step 2 until (12.14) is no longer decreasing. Determining whether (12.14) is decreasing requires us only to keep track of mssold - mss. However, in practice, we keep track of (mssold - mss) / mss0 instead: this makes it so that the number of iterations required for Algorithm 12.1 to converge does not depend on whether we multiplied the raw data X by a constant factor.
542 12. Unsupervised Learning
Iteration: 1, MSS:0.395, Rel.Err 5.99e-01
Iteration: 2, MSS:0.382, Rel.Err 1.33e-02
Iteration: 3, MSS:0.381, Rel.Err 1.44e-03
Iteration: 4, MSS:0.381, Rel.Err 1.79e-04
Iteration: 5, MSS:0.381, Rel.Err 2.58e-05
Iteration: 6, MSS:0.381, Rel.Err 4.22e-06
Iteration: 7, MSS:0.381, Rel.Err 7.65e-07
Iteration: 8, MSS:0.381, Rel.Err 1.48e-07
Iteration: 9, MSS:0.381, Rel.Err 2.95e-08We see that after eight iterations, the relative error has fallen below thresh = 1e-7, and so the algorithm terminates. When this happens, the mean squared error of the non-missing elements equals 0.381.
Finally, we compute the correlation between the 20 imputed values and the actual values:
In [31]: np.corrcoef(Xapp[ismiss], X[ismiss])[0,1]
Out[31]: 0.711
In this lab, we implemented Algorithm 12.1 ourselves for didactic purposes. However, a reader who wishes to apply matrix completion to their data might look to more specialized Python implementations.
12.5.3 Clustering
K-Means Clustering
The estimator sklearn.cluster.KMeans() performs K-means clustering in Kmeans() Python. We begin with a simple simulated example in which there truly are two clusters in the data: the frst 25 observations have a mean shift relative to the next 25 observations.
In [32]: np.random.seed(0);
X = np.random.standard_normal((50,2));
X[:25,0] += 3;
X[:25,1] -= 4;We now perform K-means clustering with K = 2.
In [33]: kmeans = KMeans(n_clusters=2,
random_state=2,n_init=20).fit(X) We specify random_state to make the results reproducible. The cluster as-
signments of the 50 observations are contained in kmeans.labels_.
In [34]: kmeans.labels_Out[34]: array([1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 0, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], dtype=int32)The K-means clustering perfectly separated the observations into two clusters even though we did not supply any group information to KMeans(). We can plot the data, with each observation colored according to its cluster assignment.
In [35]: fig, ax = plt.subplots(1, 1, figsize=(8,8))
ax.scatter(X[:,0], X[:,1], c=kmeans.labels_)
ax.set_title("K-Means Clustering Results with K=2");Here the observations can be easily plotted because they are two-dimensional. If there were more than two variables then we could instead perform PCA and plot the frst two principal component score vectors to represent the clusters.
In this example, we knew that there really were two clusters because we generated the data. However, for real data, we do not know the true number of clusters, nor whether they exist in any precise way. We could instead have performed K-means clustering on this example with K = 3.
In [36]: kmeans = KMeans(n_clusters=3,random_state=3,
n_init=20).fit(X)
fig, ax = plt.subplots(figsize=(8,8))
ax.scatter(X[:,0], X[:,1], c=kmeans.labels_)
ax.set_title("K-Means Clustering Results with K=3");When K = 3, K-means clustering splits up the two clusters. We have used the n_init argument to run the K-means with 20 initial cluster assignments (the default is 10). If a value of n_init greater than one is used, then Kmeans clustering will be performed using multiple random assignments in Step 1 of Algorithm 12.2, and the KMeans() function will report only the best results. Here we compare using n_init=1 to n_init=20.
In [37]: kmeans1 = KMeans(n_clusters=3,
random_state=3,
n_init=1).fit(X)
kmeans20 = KMeans(n_clusters=3,
random_state=3,
n_init=20).fit(X);
kmeans1.inertia_, kmeans20.inertia_Out[37]: (78.06, 75.04)
Note that kmeans.inertia_ is the total within-cluster sum of squares, which we seek to minimize by performing K-means clustering (12.17).
We strongly recommend always running K-means clustering with a large value of n_init, such as 20 or 50, since otherwise an undesirable local optimum may be obtained.
When performing K-means clustering, in addition to using multiple initial cluster assignments, it is also important to set a random seed using the random_state argument to KMeans(). This way, the initial cluster assignments in Step 1 can be replicated, and the K-means output will be fully reproducible.
Hierarchical Clustering
The AgglomerativeClustering() class from the sklearn.clustering pack- Agglomerative Clustering() age implements hierarchical clustering. As its name is long, we use the short hand HClust for hierarchical clustering. Note that this will not change
the return type when using this method, so instances will still be of class AgglomerativeClustering. In the following example we use the data from the previous lab to plot the hierarchical clustering dendrogram using complete, single, and average linkage clustering with Euclidean distance as the dissimilarity measure. We begin by clustering observations using complete linkage.
In [38]: HClust = AgglomerativeClustering
hc_comp = HClust(distance_threshold=0,
n_clusters=None,
linkage='complete')
hc_comp.fit(X)This computes the entire dendrogram. We could just as easily perform hierarchical clustering with average or single linkage instead:
In [39]: hc_avg = HClust(distance_threshold=0,
n_clusters=None,
linkage='average');
hc_avg.fit(X)
hc_sing = HClust(distance_threshold=0,
n_clusters=None,
linkage='single');
hc_sing.fit(X);To use a precomputed distance matrix, we provide an additional argument metric=“precomputed”. In the code below, the frst four lines computes the 50 × 50 pairwise-distance matrix.
In [40]: D = np.zeros((X.shape[0], X.shape[0]));
for i in range(X.shape[0]):
x_ = np.multiply.outer(np.ones(X.shape[0]), X[i])
D[i] = np.sqrt(np.sum((X - x_)**2, 1));
hc_sing_pre = HClust(distance_threshold=0,
n_clusters=None,
metric='precomputed',
linkage='single')
hc_sing_pre.fit(D)We use dendrogram() from scipy.cluster.hierarchy to plot the dendro- dendrogram() gram. However, dendrogram() expects a so-called linkage-matrix representation of the clustering, which is not provided by AgglomerativeClustering(), but can be computed. The function compute_linkage() in the ISLP.cluster compute_ package is provided for this purpose.
linkage() ISLP.cluster
We can now plot the dendrograms. The numbers at the bottom of the plot identify each observation. The dendrogram() function has a default method to color diferent branches of the tree that suggests a pre-defned cut of the tree at a particular depth. We prefer to overwrite this default by setting this threshold to be infnite. Since we want this behavior for many dendrograms, we store these values in a dictionary cargs and pass this as keyword arguments using the notation **cargs.
In [41]: cargs = {'color_threshold':-np.inf,
'above_threshold_color':'black'}
linkage_comp = compute_linkage(hc_comp)
fig, ax = plt.subplots(1, 1, figsize=(8, 8))dendrogram(linkage_comp,
ax=ax,
**cargs);We may want to color branches of the tree above and below a cutthreshold diferently. This can be achieved by changing the color_threshold. Let’s cut the tree at a height of 4, coloring links that merge above 4 in black.
In [42]: fig, ax = plt.subplots(1, 1, figsize=(8, 8))
dendrogram(linkage_comp,
ax=ax,
color_threshold=4,
above_threshold_color='black');To determine the cluster labels for each observation associated with a given cut of the dendrogram, we can use the cut_tree() function from cut_tree() scipy.cluster.hierarchy:
In [43]: cut_tree(linkage_comp, n_clusters=4).TOut[43]: array([[0, 1, 0, 0, 1, 1, 0, 1, 0, 0, 2, 0, 0, 0, 1, 1, 0, 0, 1,
0, 0, 2, 0, 2, 2, 3, 2, 3, 3, 3, 3, 2, 3, 3, 3, 3, 2, 3,
3, 3, 3, 2, 3, 3, 3, 3, 3, 3, 3, 3]])This can also be achieved by providing an argument n_clusters to HClust(); however each cut would require recomputing the clustering. Similarly, trees may be cut by distance threshold with an argument of distance_threshold to HClust() or height to cut_tree().
In [44]: cut_tree(linkage_comp, height=5)Out[44]: array([[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 1, 1, 2, 1, 2, 2, 2, 2, 1, 2, 2, 2, 2, 1, 2, 2, 2, 2, 1, 2, 2, 2, 2, 2, 2, 2, 2]])
To scale the variables before performing hierarchical clustering of the observations, we use StandardScaler() as in our PCA example:
In [45]: scaler = StandardScaler()
X_scale = scaler.fit_transform(X)
hc_comp_scale = HClust(distance_threshold=0,
n_clusters=None,
linkage='complete').fit(X_scale)
linkage_comp_scale = compute_linkage(hc_comp_scale)
fig, ax = plt.subplots(1, 1, figsize=(8, 8))
dendrogram(linkage_comp_scale , ax=ax, **cargs)
ax.set_title("Hierarchical Clustering with Scaled Features");Correlation-based distances between observations can be used for clustering. The correlation between two observations measures the similarity of their feature values.10 With n observations, the n×n correlation matrix
10Suppose each observation has p features, each a single numerical value. We measure the similarity of two such observations by computing the correlation of these p pairs of numbers.
can then be used as a similarity (or afnity) matrix, i.e. so that one minus the correlation matrix is the dissimilarity matrix used for clustering.
Note that using correlation only makes sense for data with at least three features since the absolute correlation between any two observations with measurements on two features is always one. Hence, we will cluster a threedimensional data set.
In [46]: X = np.random.standard_normal((30, 3))
corD = 1 - np.corrcoef(X)
hc_cor = HClust(linkage='complete',
distance_threshold=0,
n_clusters=None,
metric='precomputed')
hc_cor.fit(corD)
linkage_cor = compute_linkage(hc_cor)
fig, ax = plt.subplots(1, 1, figsize=(8, 8))
dendrogram(linkage_cor , ax=ax, **cargs)
ax.set_title("Complete Linkage with Correlation-Based Dissimilarity
");12.5.4 NCI60 Data Example
Unsupervised techniques are often used in the analysis of genomic data. In particular, PCA and hierarchical clustering are popular tools. We illustrate these techniques on the NCI60 cancer cell line microarray data, which consists of 6830 gene expression measurements on 64 cancer cell lines.
In [47]: NCI60 = load_data('NCI60')
nci_labs = NCI60['labels']
nci_data = NCI60['data']Each cell line is labeled with a cancer type. We do not make use of the cancer types in performing PCA and clustering, as these are unsupervised techniques. But after performing PCA and clustering, we will check to see the extent to which these cancer types agree with the results of these unsupervised techniques.
The data has 64 rows and 6830 columns.
In [48]: nci_data.shape
Out[48]: (64, 6830)
We begin by examining the cancer types for the cell lines.
In [49]: nci_labs.value_counts()
Out[49]: label
NSCLC 9
RENAL 9
MELANOMA 8
BREAST 7
COLON 7
LEUKEMIA 6
OVARIAN 6CNS 5
PROSTATE 2
K562A-repro 1
K562B-repro 1
MCF7A-repro 1
MCF7D-repro 1
UNKNOWN 1
dtype: int64PCA on the NCI60 Data
We frst perform PCA on the data after scaling the variables (genes) to have standard deviation one, although here one could reasonably argue that it is better not to scale the genes as they are measured in the same units.
In [50]: scaler = StandardScaler()
nci_scaled = scaler.fit_transform(nci_data)
nci_pca = PCA()
nci_scores = nci_pca.fit_transform(nci_scaled)We now plot the frst few principal component score vectors, in order to visualize the data. The observations (cell lines) corresponding to a given cancer type will be plotted in the same color, so that we can see to what extent the observations within a cancer type are similar to each other.
In [51]: cancer_types = list(np.unique(nci_labs))
nci_groups = np.array([cancer_types.index(lab)
for lab in nci_labs.values])
fig, axes = plt.subplots(1, 2, figsize=(15,6))
ax = axes[0]
ax.scatter(nci_scores[:,0],
nci_scores[:,1],
c=nci_groups,
marker='o',
s=50)
ax.set_xlabel('PC1'); ax.set_ylabel('PC2')
ax = axes[1]
ax.scatter(nci_scores[:,0],
nci_scores[:,2],
c=nci_groups,
marker='o',
s=50)
ax.set_xlabel('PC1'); ax.set_ylabel('PC3');The resulting plots are shown in Figure 12.17. On the whole, cell lines corresponding to a single cancer type do tend to have similar values on the frst few principal component score vectors. This indicates that cell lines from the same cancer type tend to have pretty similar gene expression levels.
We can also plot the percent variance explained by the principal components as well as the cumulative percent variance explained. This is similar to the plots we made earlier for the USArrests data.
In [52]: fig, axes = plt.subplots(1, 2, figsize=(15,6))
ax = axes[0]
ticks = np.arange(nci_pca.n_components_)+1
FIGURE 12.17. Projections of the NCI60 cancer cell lines onto the frst three principal components (in other words, the scores for the frst three principal components). On the whole, observations belonging to a single cancer type tend to lie near each other in this low-dimensional space. It would not have been possible to visualize the data without using a dimension reduction method such as PCA, since based on the full data set there are (6,830 2 ) possible scatterplots, none of which would have been particularly informative.
ax.plot(ticks,
nci_pca.explained_variance_ratio_,
marker='o')
ax.set_xlabel('Principal Component');
ax.set_ylabel('PVE')
ax = axes[1]
ax.plot(ticks,
nci_pca.explained_variance_ratio_.cumsum(),
marker='o');
ax.set_xlabel('Principal Component')
ax.set_ylabel('Cumulative PVE');The resulting plots are shown in Figure 12.18.
We see that together, the frst seven principal components explain around 40% of the variance in the data. This is not a huge amount of the variance. However, looking at the scree plot, we see that while each of the frst seven principal components explain a substantial amount of variance, there is a marked decrease in the variance explained by further principal components. That is, there is an elbow in the plot after approximately the seventh principal component. This suggests that there may be little beneft to examining more than seven or so principal components (though even examining seven principal components may be difcult).
Clustering the Observations of the NCI60 Data
We now perform hierarchical clustering of the cell lines in the NCI60 data using complete, single, and average linkage. Once again, the goal is to fnd out whether or not the observations cluster into distinct types of cancer. Euclidean distance is used as the dissimilarity measure. We frst write a short function to produce the three dendrograms.
FIGURE 12.18. The PVE of the principal components of the NCI60 cancer cell line microarray data set. Left: the PVE of each principal component is shown. Right: the cumulative PVE of the principal components is shown. Together, all principal components explain 100,% of the variance.
In [53]: def plot_nci(linkage , ax, cut=-np.inf):
cargs = {'above_threshold_color':'black',
'color_threshold':cut}
hc = HClust(n_clusters=None,
distance_threshold=0,
linkage=linkage.lower()).fit(nci_scaled)
linkage_ = compute_linkage(hc)
dendrogram(linkage_,
ax=ax,
labels=np.asarray(nci_labs),
leaf_font_size=10,
**cargs)
ax.set_title('%s Linkage' % linkage)
return hcLet’s plot our results.
In [54]: fig, axes = plt.subplots(3, 1, figsize=(15,30))
ax = axes[0]; hc_comp = plot_nci('Complete', ax)
ax = axes[1]; hc_avg = plot_nci('Average', ax)
ax = axes[2]; hc_sing = plot_nci('Single', ax)The results are shown in Figure 12.19. We see that the choice of linkage certainly does afect the results obtained. Typically, single linkage will tend to yield trailing clusters: very large clusters onto which individual observations attach one-by-one. On the other hand, complete and average linkage tend to yield more balanced, attractive clusters. For this reason, complete and average linkage are generally preferred to single linkage. Clearly cell lines within a single cancer type do tend to cluster together, although the clustering is not perfect. We will use complete linkage hierarchical clustering for the analysis that follows.
FIGURE 12.19. The NCI60 cancer cell line microarray data, clustered with average, complete, and single linkage, and using Euclidean distance as the dissimilarity measure. Complete and average linkage tend to yield evenly sized clusters whereas single linkage tends to yield extended clusters to which single leaves are fused one by one.
We can cut the dendrogram at the height that will yield a particular number of clusters, say four:
In [55]: linkage_comp = compute_linkage(hc_comp)
comp_cut = cut_tree(linkage_comp , n_clusters=4).reshape(-1)
pd.crosstab(nci_labs['label'],
pd.Series(comp_cut.reshape(-1), name='Complete'))There are some clear patterns. All the leukemia cell lines fall in one cluster, while the breast cancer cell lines are spread out over three diferent clusters.
We can plot a cut on the dendrogram that produces these four clusters:
In [56]: fig, ax = plt.subplots(figsize=(10,10))
plot_nci('Complete', ax, cut=140)
ax.axhline(140, c='r', linewidth=4);The axhline() function draws a horizontal line line on top of any existing set of axes. The argument 140 plots a horizontal line at height 140 on the dendrogram; this is a height that results in four distinct clusters. It is easy to verify that the resulting clusters are the same as the ones we obtained in comp_cut.
We claimed earlier in Section 12.4.2 that K-means clustering and hierarchical clustering with the dendrogram cut to obtain the same number of clusters can yield very diferent results. How do these NCI60 hierarchical clustering results compare to what we get if we perform K-means clustering with K = 4?
In [57]: nci_kmeans = KMeans(n_clusters=4,
random_state=0,
n_init=20).fit(nci_scaled)
pd.crosstab(pd.Series(comp_cut, name='HClust'),
pd.Series(nci_kmeans.labels_, name='K-means'))Out[57]: K-means 0 1 2 3
HClust
0 28 3 9 0
1 7000
2 0008
3 0900We see that the four clusters obtained using hierarchical clustering and K-means clustering are somewhat diferent. First we note that the labels in the two clusterings are arbitrary. That is, swapping the identifer of the cluster does not change the clustering. We see here Cluster 3 in K-means clustering is identical to cluster 2 in hierarchical clustering. However, the other clusters difer: for instance, cluster 0 in K-means clustering contains a portion of the observations assigned to cluster 0 by hierarchical clustering, as well as all of the observations assigned to cluster 1 by hierarchical clustering.
Rather than performing hierarchical clustering on the entire data matrix, we can also perform hierarchical clustering on the frst few principal component score vectors, regarding these frst few components as a less noisy version of the data.
552 12. Unsupervised Learning
In [58]: hc_pca = HClust(n_clusters=None,
distance_threshold=0,
linkage='complete'
).fit(nci_scores[:,:5])
linkage_pca = compute_linkage(hc_pca)
fig, ax = plt.subplots(figsize=(8,8))
dendrogram(linkage_pca,
labels=np.asarray(nci_labs),
leaf_font_size=10,
ax=ax,
**cargs)
ax.set_title("Hier. Clust. on First Five Score Vectors")
pca_labels = pd.Series(cut_tree(linkage_pca,
n_clusters=4).reshape(-1),
name='Complete-PCA')
pd.crosstab(nci_labs['label'], pca_labels)12.6 Exercises
Conceptual
- This problem involves the K-means clustering algorithm.
- Suppose that we have four observations, for which we compute a dissimilarity matrix, given by
| ⎡ | 0.3 | 0.4 | 0.7 | ⎤ | |
|---|---|---|---|---|---|
| ⎢ | 0.3 | 0.5 | 0.8 | ⎥ | |
| ⎢ ⎣ |
0.4 | 0.5 | 0.45 | ⎥ ⎦ |
|
| 0.7 | 0.8 | 0.45 |
For instance, the dissimilarity between the frst and second observations is 0.3, and the dissimilarity between the second and fourth observations is 0.8.
- On the basis of this dissimilarity matrix, sketch the dendrogram that results from hierarchically clustering these four observations using complete linkage. Be sure to indicate on the plot the height at which each fusion occurs, as well as the observations corresponding to each leaf in the dendrogram.
- Repeat (a), this time using single linkage clustering.
- Suppose that we cut the dendrogram obtained in (a) such that two clusters result. Which observations are in each cluster?
- Suppose that we cut the dendrogram obtained in (b) such that two clusters result. Which observations are in each cluster?
- It is mentioned in this chapter that at each fusion in the dendrogram, the position of the two clusters being fused can be swapped without changing the meaning of the dendrogram. Draw a dendrogram that is equivalent to the dendrogram in (a), for which two or more of the leaves are repositioned, but for which the meaning of the dendrogram is the same.
- In this problem, you will perform K-means clustering manually, with K = 2, on a small example with n = 6 observations and p = 2 features. The observations are as follows.
| Obs. | X1 | X2 |
|---|---|---|
| 1 | 1 | 4 |
| 2 | 1 | 3 |
| 3 | 0 | 4 |
| 4 | 5 | 1 |
| 5 | 6 | 2 |
| 6 | 4 | 0 |
- Plot the observations.
- Randomly assign a cluster label to each observation. You can use the np.random.choice() function to do this. Report the cluster labels for each observation.
- Compute the centroid for each cluster.
- Assign each observation to the centroid to which it is closest, in terms of Euclidean distance. Report the cluster labels for each observation.
- Repeat (c) and (d) until the answers obtained stop changing.
- In your plot from (a), color the observations according to the cluster labels obtained.
- Suppose that for a particular data set, we perform hierarchical clustering using single linkage and using complete linkage. We obtain two dendrograms.
- At a certain point on the single linkage dendrogram, the clusters {1, 2, 3} and {4, 5} fuse. On the complete linkage dendrogram, the clusters {1, 2, 3} and {4, 5} also fuse at a certain point. Which fusion will occur higher on the tree, or will they fuse at the same height, or is there not enough information to tell?
- At a certain point on the single linkage dendrogram, the clusters {5} and {6} fuse. On the complete linkage dendrogram, the clusters {5} and {6} also fuse at a certain point. Which fusion will occur higher on the tree, or will they fuse at the same height, or is there not enough information to tell?
- In words, describe the results that you would expect if you performed K-means clustering of the eight shoppers in Figure 12.16, on the basis of their sock and computer purchases, with K = 2. Give three answers, one for each of the variable scalings displayed. Explain.
- We saw in Section 12.2.2 that the principal component loading and score vectors provide an approximation to a matrix, in the sense of (12.5). Specifcally, the principal component score and loading vectors solve the optimization problem given in (12.6).
Now, suppose that the M principal component score vectors zim, m = 1,…,M, are known. Using (12.6), explain that each of the frst M principal component loading vectors φjm, m = 1,…,M, can be obtained by performing p separate least squares linear regressions. In each regression, the principal component score vectors are the predictors, and one of the features of the data matrix is the response.
Applied
- In this chapter, we mentioned the use of correlation-based distance and Euclidean distance as dissimilarity measures for hierarchical clustering. It turns out that these two measures are almost equivalent: if each observation has been centered to have mean zero and standard deviation one, and if we let rij denote the correlation between the ith and jth observations, then the quantity 1 − rij is proportional to the squared Euclidean distance between the ith and jth observations.
On the USArrests data, show that this proportionality holds.
Hint: The Euclidean distance can be calculated using the pairwise_distances() function from the sklearn.metrics module, and pairwise_ distances() correlations can be calculated using the np.corrcoef() function.
- In Section 12.2.3, a formula for calculating PVE was given in Equation 12.10. We also saw that the PVE can be obtained using the explained_variance_ratio_ attribute of a ftted PCA() estimator.
On the USArrests data, calculate PVE in two ways:
- Using the explained_variance_ratio_ output of the ftted PCA() estimator, as was done in Section 12.2.3.
These two approaches should give the same results.
Hint: You will only obtain the same results in (a) and (b) if the same data is used in both cases. For instance, if in (a) you performed PCA() using centered and scaled variables, then you must center and scale the variables before applying Equation 12.10 in (b).
- Consider the USArrests data. We will now perform hierarchical clustering on the states.
- Using hierarchical clustering with complete linkage and Euclidean distance, cluster the states.
- Cut the dendrogram at a height that results in three distinct clusters. Which states belong to which clusters?
- Hierarchically cluster the states using complete linkage and Euclidean distance, after scaling the variables to have standard deviation one.
- What efect does scaling the variables have on the hierarchical clustering obtained? In your opinion, should the variables be scaled before the inter-observation dissimilarities are computed? Provide a justifcation for your answer.
- In this problem, you will generate simulated data, and then perform PCA and K-means clustering on the data.
- Generate a simulated data set with 20 observations in each of three classes (i.e. 60 observations total), and 50 variables. Hint: There are a number of functions in Python that you can use to generate data. One example is the normal() method of the random() function in numpy; the uniform() method is another option. Be sure to add a mean shift to the observations in each class so that there are three distinct classes.
- Perform PCA on the 60 observations and plot the frst two principal component score vectors. Use a diferent color to indicate the observations in each of the three classes. If the three classes appear separated in this plot, then continue on to part (c). If not, then return to part (a) and modify the simulation so that there is greater separation between the three classes. Do not continue to part (c) until the three classes show at least some separation in the frst two principal component score vectors.
- Perform K-means clustering of the observations with K = 3. How well do the clusters that you obtained in K-means clustering compare to the true class labels?
Hint: You can use the pd.crosstab() function in Python to compare the true class labels to the class labels obtained by clustering. Be careful how you interpret the results: K-means clustering will arbitrarily number the clusters, so you cannot simply check whether the true class labels and clustering labels are the same.
- Perform K-means clustering with K = 2. Describe your results.
- Now perform K-means clustering with K = 4, and describe your results.
- Now perform K-means clustering with K = 3 on the frst two principal component score vectors, rather than on the raw data. That is, perform K-means clustering on the 60 × 2 matrix of which the frst column is the frst principal component score vector, and the second column is the second principal component score vector. Comment on the results.
- Using the StandardScaler() estimator, perform K-means clustering with K = 3 on the data after scaling each variable to have standard deviation one. How do these results compare to those obtained in (b)? Explain.
- Write a Python function to perform matrix completion as in Algorithm 12.1, and as outlined in Section 12.5.2. In each iteration, the function should keep track of the relative error, as well as the iteration count. Iterations should continue until the relative error is small enough or until some maximum number of iterations is reached (set a default value for this maximum number). Furthermore, there should be an option to print out the progress in each iteration.
Test your function on the Boston data. First, standardize the features to have mean zero and standard deviation one using the StandardScaler() function. Run an experiment where you randomly leave out an increasing (and nested) number of observations from 5% to 30%, in steps of 5%. Apply Algorithm 12.1 with M = 1, 2,…, 8. Display the approximation error as a function of the fraction of observations that are missing, and the value of M, averaged over 10 repetitions of the experiment.
- In Section 12.5.2, Algorithm 12.1 was implemented using the svd() function from the np.linalg module. However, given the connection between the svd() function and the PCA() estimator highlighted in the lab, we could have instead implemented the algorithm using PCA().
Write a function to implement Algorithm 12.1 that makes use of PCA() rather than svd().
- On the book website, www.statlearning.com, there is a gene expression data set (Ch12Ex13.csv) that consists of 40 tissue samples with measurements on 1,000 genes. The frst 20 samples are from healthy patients, while the second 20 are from a diseased group.
- Load in the data using pd.read_csv(). You will need to select header = None.
- Apply hierarchical clustering to the samples using correlationbased distance, and plot the dendrogram. Do the genes separate the samples into the two groups? Do your results depend on the type of linkage used?
- Your collaborator wants to know which genes difer the most across the two groups. Suggest a way to answer this question, and apply it here.
13 Multiple Testing

Thus far, this textbook has mostly focused on estimation and its close cousin, prediction. In this chapter, we instead focus on hypothesis testing, which is key to conducting inference. We remind the reader that inference was briefy discussed in Chapter 2.
While Section 13.1 provides a brief review of null hypotheses, p-values, test statistics, and other key ideas in hypothesis testing, this chapter assumes that the reader has had previous exposure to these topics. In particular, we will not focus on why or how to conduct a hypothesis test — a topic on which entire books can be (and have been) written! Instead, we will assume that the reader is interested in testing some particular set of null hypotheses, and has a specifc plan in mind for how to conduct the tests and obtain p-values.
Much of the emphasis in classical statistics focuses on testing a single null hypothesis, such as H0: the expected blood pressure of mice in the control group equals the expected blood pressure of mice in the treatment group. Of course, we would probably like to discover that there is a diference between the mean blood pressure in the two groups. But for reasons that will become clear, we construct a null hypothesis corresponding to no diference.
In contemporary settings, we are often faced with huge amounts of data, and consequently may wish to test a great many null hypotheses. For instance, rather than simply testing H0, we might want to test m null hypotheses, H01,…,H0m, where H0j : the expected value of the jth biomarker among mice in the control group equals the expected value of the jth biomarker among mice in the treatment group. When conducting multiple testing, we need to be very careful about how we interpret the results, in order to avoid erroneously rejecting far too many null hypotheses.
This chapter discusses classical as well as more contemporary ways to conduct multiple testing in a big-data setting. In Section 13.2, we highlight the challenges associated with multiple testing. Classical solutions to these
© Springer Nature Switzerland AG 2023
challenges are presented in Section 13.3, and more contemporary solutions in Sections 13.4 and 13.5.
In particular, Section 13.4 focuses on the false discovery rate. The notion of the false discovery rate dates back to the 1990s. It quickly rose in popularity in the early 2000s, when large-scale data sets began to come out of genomics. These datasets were unique not only because of their large size,1 but also because they were typically collected for exploratory purposes: researchers collected these datasets in order to test a huge number of null hypotheses, rather than just a very small number of pre-specifed null hypotheses. Today, of course, huge datasets are collected without a pre-specifed null hypothesis across virtually all felds. As we will see, the false discovery rate is perfectly-suited for this modern-day reality.
This chapter naturally centers upon the classical statistical technique of p-values, used to quantify the results of hypothesis tests. At the time of writing of this book (2020), p-values have recently been the topic of extensive commentary in the social science research community, to the extent that some social science journals have gone so far as to ban the use of p-values altogether! We will simply comment that when properly understood and applied, p-values provide a powerful tool for drawing inferential conclusions from our data.
13.1 A Quick Review of Hypothesis Testing
Hypothesis tests provide a rigorous statistical framework for answering simple “yes-or-no” questions about data, such as the following:
- Is the true coefcient βj in a linear regression of Y onto X1,…,Xp equal to zero?2
- Is there a diference in the expected blood pressure of laboratory mice in the control group and laboratory mice in the treatment group?3
In Section 13.1.1, we briefy review the steps involved in hypothesis testing. Section 13.1.2 discusses the diferent types of mistakes, or errors, that can occur in hypothesis testing.
13.1.1 Testing a Hypothesis
Conducting a hypothesis test typically proceeds in four steps. First, we defne the null and alternative hypotheses. Next, we construct a test statistic that summarizes the strength of evidence against the null hypothesis. We then compute a p-value that quantifes the probability of having obtained
1Microarray data was viewed as “big data” at the time, although by today’s standards, this label seems quaint: a microarray dataset can be (and typically was) stored in a Microsoft Excel spreadsheet!
2This hypothesis test was discussed on page 76 of Chapter 3.
3The “treatment group” refers to the set of mice that receive an experimental treatment, and the “control group” refers to those that do not.
a comparable or more extreme value of the test statistic under the null hypothesis. Finally, based on the p-value, we decide whether to reject the null hypothesis. We now briefy discuss each of these steps in turn.
Step 1: Defne the Null and Alternative Hypotheses
In hypothesis testing, we divide the world into two possibilities: the null hypothesis and the alternative hypothesis. The null hypothesis, denoted H0, null is the default state of belief about the world.4 For instance, null hypotheses associated with the two questions posed earlier in this chapter are as follows:
hypothesis alternative hypothesis
- The true coefcient βj in a linear regression of Y onto X1,…,Xp equals zero.
- There is no diference between the expected blood pressure of mice in the control and treatment groups.
The null hypothesis is boring by construction: it may well be true, but we might hope that our data will tell us otherwise.
The alternative hypothesis, denoted Ha, represents something diferent and unexpected: for instance, that there is a diference between the expected blood pressure of the mice in the two groups. Typically, the alternative hypothesis simply posits that the null hypothesis does not hold: if the null hypothesis states that there is no diference between A and B, then the alternative hypothesis states that there is a diference between A and B.
It is important to note that the treatment of H0 and Ha is asymmetric. H0 is treated as the default state of the world, and we focus on using data to reject H0. If we reject H0, then this provides evidence in favor of Ha. We can think of rejecting H0 as making a discovery about our data: namely, we are discovering that H0 does not hold! By contrast, if we fail to reject H0, then our fndings are more nebulous: we will not know whether we failed to reject H0 because our sample size was too small (in which case testing H0 again on a larger or higher-quality dataset might lead to rejection), or whether we failed to reject H0 because H0 really holds.
Step 2: Construct the Test Statistic
Next, we wish to use our data in order to fnd evidence for or against the null hypothesis. In order to do this, we must compute a test statistic, test statistic denoted T, which summarizes the extent to which our data are consistent with H0. The way in which we construct T depends on the nature of the null hypothesis that we are testing.
To make things concrete, let xt 1,…,xt nt denote the blood pressure measurements for the nt mice in the treatment group, and let xc 1,…,xc nc denote the blood pressure measurements for the nc mice in the control group, and µt = E(Xt ), µc = E(Xc). To test H0 : µt = µc, we make use of a two-sample t-statistic, 5 defned as two-sample
t-statistic
4H0 is pronounced “H naught” or “H zero”.
FIGURE 13.1. The density function for the N(0, 1) distribution, with the vertical line indicating a value of 2.33. 1% of the area under the curve falls to the right of the vertical line, so there is only a 2% chance of observing a N(0, 1) value that is greater than 2.33 or less than −2.33. Therefore, if a test statistic has a N(0, 1) null distribution, then an observed test statistic of T = 2.33 leads to a p-value of 0.02.
\[T = \frac{\hat{\mu}\_t - \hat{\mu}\_c}{s\sqrt{\frac{1}{n\_t} + \frac{1}{n\_c}}}\tag{13.1}\]
where µˆt = 1 nt #nt i=1 xt i, µˆc = 1 nc #nc i=1 xc i , and
\[s = \sqrt{\frac{(n\_t - 1)s\_t^2 + (n\_c - 1)s\_c^2}{n\_t + n\_c - 2}}\tag{13.2}\]
is an estimator of the pooled standard deviation of the two samples.6 Here, s2 t and s2 c are unbiased estimators of the variance of the blood pressure in the treatment and control groups, respectively. A large (absolute) value of T provides evidence against H0 : µt = µc, and hence evidence in support of Ha : µt ≠ µc.
Step 3: Compute the p-Value
In the previous section, we noted that a large (absolute) value of a twosample t-statistic provides evidence against H0. This begs the question: how large is large? In other words, how much evidence against H0 is provided by a given value of the test statistic?
The notion of a p-value provides us with a way to formalize as well as p-value answer this question. The p-value is defned as the probability of observing a test statistic equal to or more extreme than the observed statistic, under the assumption that H0 is in fact true. Therefore, a small p-value provides evidence against H0.
5The t-statistic derives its name from the fact that, under H0, it follows a tdistribution.
6Note that (13.2) assumes that the control and treatment groups have equal variance. Without this assumption, (13.2) would take a slightly diferent form.
To make this concrete, suppose that T = 2.33 for the test statistic in (13.1). Then, we can ask: what is the probability of having observed such a large value of T, if indeed H0 holds? It turns out that under H0, the distribution of T in (13.1) follows approximately a N(0, 1) distribution7 that is, a normal distribution with mean 0 and variance 1. This distribution is displayed in Figure 13.1. We see that the vast majority — 98% — of the N(0, 1) distribution falls between −2.33 and 2.33. This means that under H0, we would expect to see such a large value of |T| only 2% of the time. Therefore, the p-value corresponding to T = 2.33 is 0.02.
The distribution of the test statistic under H0 (also known as the test statistic’s null distribution) will depend on the details of what type of null distribution null hypothesis is being tested, and what type of test statistic is used. In general, most commonly-used test statistics follow a well-known statistical distribution under the null hypothesis — such as a normal distribution, a t-distribution, a χ2-distribution, or an F-distribution — provided that the sample size is sufciently large and that some other assumptions hold. Typically, the R function that is used to compute a test statistic will make use of this null distribution in order to output a p-value. In Section 13.5, we will see an approach to estimate the null distribution of a test statistic using re-sampling; in many contemporary settings, this is a very attractive option, as it exploits the availability of fast computers in order to avoid having to make potentially problematic assumptions about the data.
The p-value is perhaps one of the most used and abused notions in all of statistics. In particular, it is sometimes said that the p-value is the probability that H0 holds, i.e., that the null hypothesis is true. This is not correct! The one and only correct interpretation of the p-value is as the fraction of the time that we would expect to see such an extreme value of the test statistic8 if we repeated the experiment many many times, provided H0 holds.
In Step 2 we computed a test statistic, and noted that a large (absolute) value of the test statistic provides evidence against H0. In Step 3 the test statistic was converted to a p-value, with small p-values providing evidence against H0. What, then, did we accomplish by converting the test statistic from Step 2 into a p-value in Step 3? To answer this question, suppose a data analyst conducts a statistical test, and reports a test statistic of T = 17.3. Does this provide strong evidence against H0? It’s impossible to know, without more information: in particular, we would need to know
7More precisely, assuming that the observations are drawn from a normal distribution, then T follows a t-distribution with nt + nc − 2 degrees of freedom. Provided that nt + nc − 2 is larger than around 40, this is very well-approximated by a N(0, 1) distribution. In Section 13.5, we will see an alternative and often more attractive way to approximate the null distribution of T, which avoids making stringent assumptions about the data.
8A one-sided p-value is the probability of seeing such an extreme value of the test statistic; e.g. the probability of seeing a test statistic greater than or equal to T = 2.33. A two-sided p-value is the probability of seeing such an extreme value of the absolute test statistic; e.g. the probability of seeing a test statistic greater than or equal to 2.33 or less than or equal to −2.33. The default recommendation is to report a two-sided p-value rather than a one-sided p-value, unless there is a clear and compelling reason that only one direction of the test statistic is of scientifc interest.
562 13. Multiple Testing
| Truth | ||||
|---|---|---|---|---|
| H0 | Ha | |||
| Decision | Reject H0 |
Type I Error | Correct | |
| Do Not Reject H0 |
Correct | Type II Error |
TABLE 13.1. A summary of the possible scenarios associated with testing the null hypothesis H0. Type I errors are also known as false positives, and Type II errors as false negatives.
what value of the test statistic should be expected, under H0. This is exactly what a p-value gives us. In other words, a p-value allows us to transform our test statistic, which is measured on some arbitrary and uninterpretable scale, into a number between 0 and 1 that can be more easily interpreted.
Step 4: Decide Whether to Reject the Null Hypothesis
Once we have computed a p-value corresponding to H0, it remains for us to decide whether or not to reject H0. (We do not usually talk about “accepting” H0: instead, we talk about “failing to reject” H0.) A small pvalue indicates that such a large value of the test statistic is unlikely to occur under H0, and thereby provides evidence against H0. If the p-value is sufciently small, then we will want to reject H0 (and, therefore, make a “discovery”). But how small is small enough to reject H0?
It turns out that the answer to this question is very much in the eyes of the beholder, or more specifcally, the data analyst. The smaller the pvalue, the stronger the evidence against H0. In some felds, it is typical to reject H0 if the p-value is below 0.05; this means that, if H0 holds, we would expect to see such a small p-value no more than 5% of the time.9 However, in other felds, a much higher burden of proof is required: for example, in some areas of physics, it is typical to reject H0 only if the p-value is below 10−9!
In the example displayed in Figure 13.1, if we use a threshold of 0.05 as our cut-of for rejecting the null hypothesis, then we will reject the null. By contrast, if we use a threshold of 0.01, then we will fail to reject the null. These ideas are formalized in the next section.
13.1.2 Type I and Type II Errors
If the null hypothesis holds, then we say that it is a true null hypothesis; true null hypothesis otherwise, it is a false null hypothesis. For instance, if we test H0 : µt = µc as in Section 13.1.1, and there is indeed no diference in the population mean blood pressure for mice in the treatment group and mice in the control group, then H0 is true; otherwise, it is false. Of course, we do not know a priori whether H0 is true or whether it is false: this is why we need to conduct a hypothesis test!
false null hypothesis
9Though a threshold of 0.05 to reject H0 is ubiquitous in some areas of science, we advise against blind adherence to this arbitrary choice. Furthermore, a data analyst should typically report the p-value itself, rather than just whether or not it exceeds a specifed threshold value.
Table 13.1 summarizes the possible scenarios associated with testing the null hypothesis H0. 10 Once the hypothesis test is performed, the row of the table is known (based on whether or not we have rejected H0); however, it is impossible for us to know which column we are in. If we reject H0 when H0 is false (i.e., when Ha is true), or if we do not reject H0 when it is true, then we arrived at the correct result. However, if we erroneously reject H0 when H0 is in fact true, then we have committed a Type I error. The Type I Type I error error rate is defned as the probability of making a Type I error given that Type I error H rate 0 holds, i.e., the probability of incorrectly rejecting H0. Alternatively, if we do not reject H0 when H0 is in fact false, then we have committed a Type II error. The power of the hypothesis test is defned as the probability Type II of not making a Type II error given that Ha holds, i.e., the probability of correctly rejecting H0.
error power
Ideally we would like both the Type I and Type II error rates to be small. But in practice, this is hard to achieve! There typically is a trade-of: we can make the Type I error small by only rejecting H0 if we are quite sure that it doesn’t hold; however, this will result in an increase in the Type II error. Alternatively, we can make the Type II error small by rejecting H0 in the presence of even modest evidence that it does not hold, but this will cause the Type I error to be large. In practice, we typically view Type I errors as more “serious” than Type II errors, because the former involves declaring a scientifc fnding that is not correct. Hence, when we perform hypothesis testing, we typically require a low Type I error rate — e.g., at most α = 0.05 — while trying to make the Type II error small (or, equivalently, the power large).
It turns out that there is a direct correspondence between the p-value threshold that causes us to reject H0, and the Type I error rate. By only rejecting H0 when the p-value is below α, we ensure that the Type I error rate will be less than or equal to α.
13.2 The Challenge of Multiple Testing
In the previous section, we saw that rejecting H0 if the p-value is below (say) 0.01 provides us with a simple way to control the Type I error for H0 at level 0.01: if H0 is true, then there is no more than a 1% probability that we will reject it. But now suppose that we wish to test m null hypotheses, H01,…,H0m. Will it do to simply reject all null hypotheses for which the corresponding p-value falls below (say) 0.01? Stated another way, if we reject all null hypotheses for which the p-value falls below 0.01, then how many Type I errors should we expect to make?
As a frst step towards answering this question, consider a stockbroker who wishes to drum up new clients by convincing them of her trading
10There are parallels between Table 13.1 and Table 4.6, which has to do with the output of a binary classifer. In particular, recall from Table 4.6 that a false positive results from predicting a positive (non-null) label when the true label is in fact negative (null). This is closely related to a Type I error, which results from rejecting the null hypothesis when in fact the null hypothesis holds.
acumen. She tells 1,024 (1,024 = 210) potential new clients that she can correctly predict whether Apple’s stock price will increase or decrease for 10 days running. There are 210 possibilities for how Apple’s stock price might change over the course of these 10 days. Therefore, she emails each client one of these 210 possibilities. The vast majority of her potential clients will fnd that the stockbroker’s predictions are no better than chance (and many will fnd them to be even worse than chance). But a broken clock is right twice a day, and one of her potential clients will be really impressed to fnd that her predictions were correct for all 10 of the days! And so the stockbroker gains a new client.
What happened here? Does the stockbroker have any actual insight into whether Apple’s stock price will increase or decrease? No. How, then, did she manage to predict Apple’s stock price perfectly for 10 days running? The answer is that she made a lot of guesses, and one of them happened to be exactly right.
How does this relate to multiple testing? Suppose that we fip 1,024 fair coins11 ten times each. Then we would expect (on average) one coin to come up all tails. (There’s a 1/210 = 1/1,024 chance that any single coin will come up all tails. So if we fip 1,024 coins, then we expect one coin to come up all tails, on average.) If one of our coins comes up all tails, then we might therefore conclude that this particular coin is not fair. In fact, a standard hypothesis test for the null hypothesis that this particular coin is fair would lead to a p-value below 0.002! 12 But it would be incorrect to conclude that the coin is not fair: in fact, the null hypothesis holds, and we just happen to have gotten ten tails in a row by chance.
These examples illustrate the main challenge of multiple testing: when multiple testing testing a huge number of null hypotheses, we are bound to get some very small p-values by chance. If we make a decision about whether to reject each null hypothesis without accounting for the fact that we have performed a very large number of tests, then we may end up rejecting a great number of true null hypotheses — that is, making a large number of Type I errors.
How severe is the problem? Recall from the previous section that if we reject a single null hypothesis, H0, if its p-value is less than, say, α = 0.01, then there is a 1% chance of making a false rejection if H0 is in fact true. Now what if we test m null hypotheses, H01,…,H0m, all of which are true? There’s a 1% chance of rejecting any individual null hypothesis; therefore, we expect to falsely reject approximately 0.01 × m null hypotheses. If m = 10,000, then that means that we expect to falsely reject 100 null hypotheses by chance! That is a lot of Type I errors.
The crux of the issue is as follows: rejecting a null hypothesis if the p-value is below α controls the probability of falsely rejecting that null hypothesis at level α. However, if we do this for m null hypotheses, then the chance of falsely rejecting at least one of the m null hypotheses is quite a bit higher!
11A fair coin is one that has an equal chance of landing heads or tails.
12Recall that the p-value is the probability of observing data at least this extreme, under the null hypothesis. If the coin is fair, then the probability of observing at least ten tails is (1/2)10 = 1/1,024 < 0.001. The p-value is therefore 2/1,024 < 0.002, since this is the probability of observing ten heads or ten tails.
| is True H0 |
is False H0 |
Total | |
|---|---|---|---|
| Reject H0 |
V | S | R |
| Do Not Reject H0 |
U | W | m − R |
| Total | m0 | m − m0 |
m |
TABLE 13.2. A summary of the results of testing m null hypotheses. A given null hypothesis is either true or false, and a test of that null hypothesis can either reject or fail to reject it. In practice, the individual values of V , S, U, and W are unknown. However, we do have access to V + S = R and U + W = m − R, which are the numbers of null hypotheses rejected and not rejected, respectively.
We will investigate this issue in greater detail, and pose a solution to it, in Section 13.3.
13.3 The Family-Wise Error Rate
In the following sections, we will discuss testing multiple hypotheses while controlling the probability of making at least one Type I error.
13.3.1 What is the Family-Wise Error Rate?
Recall that the Type I error rate is the probability of rejecting H0 if H0 is true. The family-wise error rate (FWER) generalizes this notion to the set- family-wise error rate ting of m null hypotheses, H01,…,H0m, and is defned as the probability of making at least one Type I error. To state this idea more formally, consider Table 13.2, which summarizes the possible outcomes when performing m hypothesis tests. Here, V represents the number of Type I errors (also known as false positives or false discoveries), S the number of true positives, U the number of true negatives, and W the number of Type II errors (also known as false negatives). Then the family-wise error rate is given by
\[\text{FWER} = \Pr(V \ge 1). \tag{13.3}\]
A strategy of rejecting any null hypothesis for which the p-value is below α (i.e. controlling the Type I error for each null hypothesis at level α) leads to a FWER of
\[\begin{aligned} \text{FWER}(\alpha) &= 1 - \Pr(V = 0) \\ &= 1 - \Pr(\text{do not falsely reject any null hypothesis}) \\ &= 1 - \Pr\left(\bigcap\_{j=1}^{m} \{\text{do not falsely reject } H\_{0j}\}\right). \end{aligned} \tag{13.4}\]
Recall from basic probability that if two events A and B are independent, then Pr(A∩B) = Pr(A) Pr(B). Therefore, if we make the additional rather strong assumptions that the m tests are independent and that all m null hypotheses are true, then
\[\text{FWER}(\alpha) = 1 - \prod\_{j=1}^{m} (1 - \alpha) = 1 - (1 - \alpha)^m. \tag{13.5}\]
FIGURE 13.2. The family-wise error rate, as a function of the number of hypotheses tested (displayed on the log scale), for three values of α: α = 0.05 (orange), α = 0.01 (blue), and α = 0.001 (purple). The dashed line indicates 0.05. For example, in order to control the FWER at 0.05 when testing m = 50 null hypotheses, we must control the Type I error for each null hypothesis at level α = 0.001.
Hence, if we test only one null hypothesis, then FWER(α)=1−(1−α)1 = α, so the Type I error rate and the FWER are equal. However, if we perform m = 100 independent tests, then FWER(α)=1 − (1 − α)100. For instance, taking α = 0.05 leads to a FWER of 1 − (1 − 0.05)100 = 0.994. In other words, we are virtually guaranteed to make at least one Type I error!
Figure 13.2 displays (13.5) for various values of m, the number of hypotheses, and α, the Type I error. We see that setting α = 0.05 results in a high FWER even for moderate m. With α = 0.01, we can test no more than fve null hypotheses before the FWER exceeds 0.05. Only for very small values, such as α = 0.001, do we manage to ensure a small FWER, at least for moderately-sized m.
We now briefy return to the example in Section 13.1.1, in which we consider testing a single null hypothesis of the form H0 : µt = µc using a two-sample t-statistic. Recall from Figure 13.1 that in order to guarantee that the Type I error does not exceed 0.02, we decide whether or not to reject H0 using a cutpoint of 2.33 (i.e. we reject H0 if |T| ≥ 2.33). Now, what if we wish to test 10 null hypotheses using two-sample t-statistics, instead of just one? We will see in Section 13.3.2 that we can guarantee that the FWER does not exceed 0.02 by rejecting only null hypotheses for which the p-value falls below 0.002. This corresponds to a much more stringent cutpoint of 3.09 (i.e. we should reject H0j only if its test statistic |Tj | ≥ 3.09, for j = 1,…, 10). In other words, controlling the FWER at level α amounts to a much higher bar, in terms of evidence required to reject any given null hypothesis, than simply controlling the Type I error for each null hypothesis at level α.
| Manager | Mean, x¯ |
Standard Deviation, s |
t-statistic | p-value |
|---|---|---|---|---|
| One | 3.0 | 7.4 | 2.86 | 0.006 |
| Two | -0.1 | 6.9 | -0.10 | 0.918 |
| Three | 2.8 | 7.5 | 2.62 | 0.012 |
| Four | 0.5 | 6.7 | 0.53 | 0.601 |
| Five | 0.3 | 6.8 | 0.31 | 0.756 |
TABLE 13.3. The frst two columns correspond to the sample mean and sample standard deviation of the percentage excess return, over n = 50 months, for the frst fve managers in the Fund dataset. The last two columns provide the t-statistic ( √n · X/S ¯ ) and associated p-value for testing H0j : µj = 0, the null hypothesis that the (population) mean return for the jth hedge fund manager equals zero.
13.3.2 Approaches to Control the Family-Wise Error Rate
In this section, we briefy survey some approaches to control the FWER. We will illustrate these approaches on the Fund dataset, which records the monthly percentage excess returns for 2,000 fund managers over n = 50 months.13 Table 13.3 provides relevant summary statistics for the frst fve managers.
We frst present the Bonferroni method and Holm’s step-down procedure, which are very general-purpose approaches for controlling the FWER that can be applied whenever m p-values have been computed, regardless of the form of the null hypotheses, the choice of test statistics, or the (in)dependence of the p-values. We then briefy discuss Tukey’s method and Schefé’s method in order to illustrate the fact that, in certain situations, more specialized approaches for controlling the FWER may be preferable.
The Bonferroni Method
As in the previous section, suppose we wish to test H01,…,H0m. Let Aj denote the event that we make a Type I error for the jth null hypothesis, for j = 1,…,m. Then
\[\begin{split} \text{FWER} &= \Pr(\text{falesly reject at least one null hypothesis}) \\ &= \Pr(\cup\_{j=1}^{m} A\_j) \\ &\leq \sum\_{j=1}^{m} \Pr(A\_j). \end{split} \tag{13.6}\]
In (13.6), the inequality results from the fact that for any two events A and B, Pr(A ∪ B) ≤ Pr(A) + Pr(B), regardless of whether A and B are independent. The Bonferroni method, or Bonferroni correction, sets the threshold for rejecting each hypothesis test to α/m, so that Pr(Aj ) ≤ α/m. Equation 13.6 implies that
\[\text{FWER}(\alpha/m) \le m \times \frac{\alpha}{m} = \alpha,\]
13Excess returns correspond to the additional return the fund manager achieves beyond the market’s overall return. So if the market increases by 5% during a given period and the fund manager achieves a 7% return, their excess return would be 7% − 5% = 2%.
so this procedure controls the FWER at level α. For instance, in order to control the FWER at level 0.1 while testing m = 100 null hypotheses, the Bonferroni procedure requires us to control the Type I error for each null hypothesis at level 0.1/100 = 0.001, i.e. to reject all null hypotheses for which the p-value is below 0.001.
We now consider the Fund dataset in Table 13.3. If we control the Type I error at level α = 0.05 for each fund manager separately, then we will conclude that the frst and third managers have signifcantly non-zero excess returns; in other words, we will reject H01 : µ1 = 0 and H03 : µ3 = 0. However, as discussed in previous sections, this procedure does not account for the fact that we have tested multiple hypotheses, and therefore it will lead to a FWER greater than 0.05. If we instead wish to control the FWER at level 0.05, then, using a Bonferroni correction, we must control the Type I error for each individual manager at level α/m = 0.05/5=0.01. Consequently, we will reject the null hypothesis only for the frst manager, since the p-values for all other managers exceed 0.01. The Bonferroni correction gives us peace of mind that we have not falsely rejected too many null hypotheses, but for a price: we reject few null hypotheses, and thus will typically make quite a few Type II errors.
The Bonferroni correction is by far the best-known and most commonlyused multiplicity correction in all of statistics. Its ubiquity is due in large part to the fact that it is very easy to understand and simple to implement, and also from the fact that it successfully controls Type I error regardless of whether the m hypothesis tests are independent. However, as we will see, it is typically neither the most powerful nor the best approach for multiple testing correction. In particular, the Bonferroni correction can be quite conservative, in the sense that the true FWER is often quite a bit lower than the nominal (or target) FWER; this results from the inequality in (13.6). By contrast, a less conservative procedure might allow us to control the FWER while rejecting more null hypotheses, and therefore making fewer Type II errors.
Holm’s Step-Down Procedure
Holm’s method, also known as Holm’s step-down procedure or the Holm– Holm’s method Bonferroni method, is an alternative to the Bonferroni procedure. Holm’s method controls the FWER, but it is less conservative than Bonferroni, in the sense that it will reject more null hypotheses, typically resulting in fewer Type II errors and hence greater power. The procedure is summarized in Algorithm 13.1. The proof that this method controls the FWER is similar to, but slightly more complicated than, the argument in (13.6) that the Bonferroni method controls the FWER. It is worth noting that in Holm’s procedure, the threshold that we use to reject each null hypothesis — p(L) in Step 5 — actually depends on the values of all m of the p-values. (See the defnition of L in (13.7).) This is in contrast to the Bonferroni procedure, in which to control the FWER at level α, we reject any null hypotheses for which the p-value is below α/m, regardless of the other p-values. Holm’s method makes no independence assumptions about the m hypothesis tests, and is uniformly more powerful than the Bonferroni method — it will
Algorithm 13.1 Holm’s Step-Down Procedure to Control the FWER
- Specify α, the level at which to control the FWER.
- Compute p-values, p1,…,pm, for the m null hypotheses H01,…,H0m.
- Order the m p-values so that p(1) ≤ p(2) ≤ ··· ≤ p(m).
- Defne
\[L = \min\left\{ j : p\_{(j)} > \frac{\alpha}{m + 1 - j} \right\}.\tag{13.7}\]
- Reject all null hypotheses H0j for which pj < p(L).
always reject at least as many null hypotheses as Bonferroni — and so it should always be preferred.
We now consider applying Holm’s method to the frst fve fund managers in the Fund dataset in Table 13.3, while controlling the FWER at level 0.05. The ordered p-values are p(1) = 0.006, p(2) = 0.012, p(3) = 0.601, p(4) = 0.756 and p(5) = 0.918. The Holm procedure rejects the frst two null hypotheses, because p(1) = 0.006 < 0.05/(5 + 1 − 1) = 0.01 and p(2) = 0.012 < 0.05/(5 + 1 − 2) = 0.0125, but p(3) = 0.601 > 0.05/(5 + 1 − 3) = 0.0167, which implies that L = 3. We note that, in this setting, Holm is more powerful than Bonferroni: the former rejects the null hypotheses for the frst and third managers, whereas the latter rejects the null hypothesis only for the frst manager.
Figure 13.3 provides an illustration of the Bonferroni and Holm methods on three simulated data sets in a setting involving m = 10 hypothesis tests, of which m0 = 2 of the null hypotheses are true. Each panel displays the ten corresponding p-values, ordered from smallest to largest, and plotted on a log scale. The eight red points represent the false null hypotheses, and the two black points represent the true null hypotheses. We wish to control the FWER at level 0.05. The Bonferroni procedure requires us to reject all null hypotheses for which the p-value is below 0.005; this is represented by the black horizontal line. The Holm procedure requires us to reject all null hypotheses that fall below the blue line. The blue line always lies above the black line, so Holm will always reject more tests than Bonferroni; the region between the two lines corresponds to the hypotheses that are only rejected by Holm. In the left-hand panel, both Bonferroni and Holm successfully reject seven of the eight false null hypotheses. In the center panel, Holm successfully rejects all eight of the false null hypotheses, while Bonferroni fails to reject one. In the right-hand panel, Bonferroni only rejects three of the false null hypotheses, while Holm rejects all eight. Neither Bonferroni nor Holm makes any Type I errors in these examples.
Two Special Cases: Tukey’s Method and Schefé’s Method
Bonferroni’s method and Holm’s method can be used in virtually any setting in which we wish to control the FWER for m null hypotheses: they
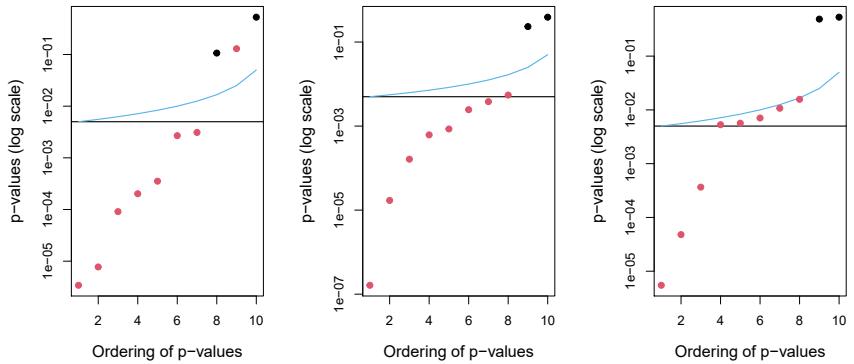
FIGURE 13.3. Each panel displays, for a separate simulation, the sorted p-values for tests of m = 10 null hypotheses. The p-values corresponding to the m0 = 2 true null hypotheses are displayed in black, and the rest are in red. When controlling the FWER at level 0.05, the Bonferroni procedure rejects all null hypotheses that fall below the black line, and the Holm procedure rejects all null hypotheses that fall below the blue line. The region between the blue and black lines indicates null hypotheses that are rejected using the Holm procedure but not using the Bonferroni procedure. In the center panel, the Holm procedure rejects one more null hypothesis than the Bonferroni procedure. In the right-hand panel, it rejects fve more null hypotheses.
make no assumptions about the nature of the null hypotheses, the type of test statistic used, or the (in)dependence of the p-values. However, in certain very specifc settings, we can achieve higher power by controlling the FWER using approaches that are more tailored to the task at hand. Tukey’s method and Schefé’s method provide two such examples.
Table 13.3 indicates that for the Fund dataset, Managers One and Two have the greatest diference in their sample mean returns. This fnding might motivate us to test the null hypothesis H0 : µ1 = µ2, where µj is the (population) mean return for the jth fund manager. A two-sample t-test (13.1) for H0 yields a p-value of 0.0349, suggesting modest evidence against H0. However, this p-value is misleading, since we decided to compare the average returns of Managers One and Two only after having examined the returns for all fve managers; this essentially amounts to having performed m = 5 × (5 − 1)/2 = 10 hypothesis tests, and selecting the one with the smallest p-value. This suggests that in order to control the FWER at level 0.05, we should make a Bonferroni correction for m = 10 hypothesis tests, and therefore should only reject a null hypothesis for which the p-value is below 0.005. If we do this, then we will be unable to reject the null hypothesis that Managers One and Two have identical performance.
However, in this setting, a Bonferroni correction is actually a bit too stringent, since it fails to consider the fact that the m = 10 hypothesis tests are all somewhat related: for instance, Managers Two and Five have similar mean returns, as do Managers Two and Four; this guarantees that the mean returns of Managers Four and Five are similar. Stated another way, the m p-values for the m pairwise comparisons are not independent. Therefore, it should be possible to control the FWER in a way that is
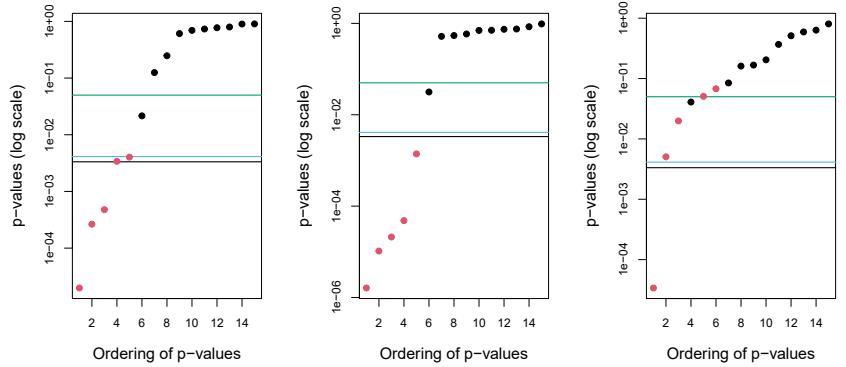
FIGURE 13.4. Each panel displays, for a separate simulation, the sorted p-values for tests of m = 15 hypotheses, corresponding to pairwise tests for the equality of G = 6 means. The m0 = 10 true null hypotheses are displayed in black, and the rest are in red. When controlling the FWER at level 0.05, the Bonferroni procedure rejects all null hypotheses that fall below the black line, whereas Tukey rejects all those that fall below the blue line. Thus, Tukey’s method has slightly higher power than Bonferroni’s method. Controlling the Type I error without adjusting for multiple testing involves rejecting all those that fall below the green line.
less conservative. This is exactly the idea behind Tukey’s method: when Tukey’s method performing m = G(G − 1)/2 pairwise comparisons of G means, it allows us to control the FWER at level α while rejecting all null hypotheses for which the p-value falls below αT , for some αT > α/m.
Figure 13.4 illustrates Tukey’s method on three simulated data sets in a setting with G = 6 means, with µ1 = µ2 = µ3 = µ4 = µ5 ≠ µ6. Therefore, of the m = G(G − 1)/2 = 15 null hypotheses of the form H0 : µj = µk, ten are true and fve are false. In each panel, the true null hypotheses are displayed in black, and the false ones are in red. The horizontal lines indicate that Tukey’s method always results in at least as many rejections as Bonferroni’s method. In the left-hand panel, Tukey correctly rejects two more null hypotheses than Bonferroni.
Now, suppose that we once again examine the data in Table 13.3, and notice that Managers One and Three have higher mean returns than Managers Two, Four, and Five. This might motivate us to test the null hypothesis
\[H\_0: \frac{1}{2} \left(\mu\_1 + \mu\_3\right) = \frac{1}{3} \left(\mu\_2 + \mu\_4 + \mu\_5\right). \tag{13.8}\]
(Recall that µj is the population mean return for the jth hedge fund manager.) It turns out that we could test (13.8) using a variant of the twosample t-test presented in (13.1), leading to a p-value of 0.004. This suggests strong evidence of a diference between Managers One and Three compared to Managers Two, Four, and Five. However, there is a problem: we decided to test the null hypothesis in (13.8) only after peeking at the data in Table 13.3. In a sense, this means that we have conducted multiple testing. In this setting, using Bonferroni to control the FWER at level α would require a p-value threshold of α/m, for an extremely large value of m14.
Schefé’s method is designed for exactly this setting. It allows us to com- Schefé’s method pute a value αS such that rejecting the null hypothesis H0 in (13.8) if the p-value is below αS will control the Type I error at level α. It turns out that for the Fund example, in order to control the Type I error at level α = 0.05, we must set αS = 0.002. Therefore, we are unable to reject H0 in (13.8), despite the apparently very small p-value of 0.004. An important advantage of Schefé’s method is that we can use this same threshold of αS = 0.002 in order to perform a pairwise comparison of any split of the managers into two groups: for instance, we could also test H0 : 1 3 (µ1 + µ2 + µ3) = 1 2 (µ4 + µ5) and H0 : 1 4 (µ1 + µ2 + µ3 + µ4) = µ5 using the same threshold of 0.002, without needing to further adjust for multiple testing.
To summarize, Holm’s procedure and Bonferroni’s procedure are very general approaches for multiple testing correction that can be applied under all circumstances. However, in certain special cases, more powerful procedures for multiple testing correction may be available, in order to control the FWER while achieving higher power (i.e. committing fewer Type II errors) than would be possible using Holm or Bonferroni. In this section, we have illustrated two such examples.
13.3.3 Trade-Of Between the FWER and Power
In general, there is a trade-of between the FWER threshold that we choose, and our power to reject the null hypotheses. Recall that power is defned as the number of false null hypotheses that we reject divided by the total number of false null hypotheses, i.e. S/(m − m0) using the notation of Table 13.2. Figure 13.5 illustrates the results of a simulation setting involving m null hypotheses, of which 90% are true and the remaining 10% are false; power is displayed as a function of the FWER. In this particular simulation setting, when m = 10, a FWER of 0.05 corresponds to power of approximately 60%. However, as m increases, the power decreases. With m = 500, the power is below 0.2 at a FWER of 0.05, so that we successfully reject only 20% of the false null hypotheses.
Figure 13.5 indicates that it is reasonable to control the FWER when m takes on a small value, like 5 or 10. However, for m = 100 or m = 1,000, attempting to control the FWER will make it almost impossible to reject any of the false null hypotheses. In other words, the power will be extremely low.
Why is this the case? Recall that, using the notation in Table 13.2, the FWER is defned as Pr(V ≥ 1) (13.3). In other other words, controlling the FWER at level α guarantees that the data analyst is very unlikely (with probability no more than α) to reject any true null hypotheses, i.e. to have any false positives. In order to make good on this guarantee when m is large, the data analyst may be forced to reject very few null hypotheses, or perhaps even none at all (since if R = 0 then also V = 0; see Table 13.2).
14In fact, calculating the “correct” value of m is quite technical, and outside the scope of this book.
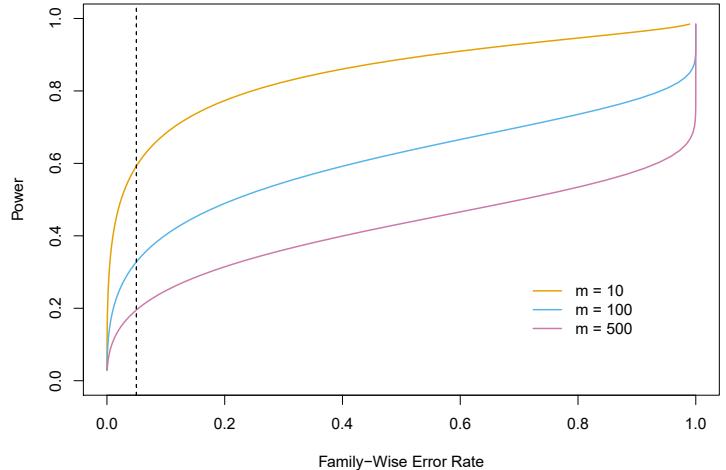
FIGURE 13.5. In a simulation setting in which 90% of the m null hypotheses are true, we display the power (the fraction of false null hypotheses that we successfully reject) as a function of the family-wise error rate. The curves correspond to m = 10 (orange), m = 100 (blue), and m = 500 (purple). As the value of m increases, the power decreases. The vertical dashed line indicates a FWER of 0.05.
This is scientifcally uninteresting, and typically results in very low power, as in Figure 13.5.
In practice, when m is large, we may be willing to tolerate a few false positives, in the interest of making more discoveries, i.e. more rejections of the null hypothesis. This is the motivation behind the false discovery rate, which we present next.
13.4 The False Discovery Rate
13.4.1 Intuition for the False Discovery Rate
As we just discussed, when m is large, then trying to prevent any false positives (as in FWER control) is simply too stringent. Instead, we might try to make sure that the ratio of false positives (V ) to total positives (V + S = R) is sufciently low, so that most of the rejected null hypotheses are not false positives. The ratio V /R is known as the false discovery proportion false (FDP).
discovery proportion
It might be tempting to ask the data analyst to control the FDP: to make sure that no more than, say, 20% of the rejected null hypotheses are false positives. However, in practice, controlling the FDP is an impossible task for the data analyst, since she has no way to be certain, on any particular dataset, which hypotheses are true and which are false. This is very similar to the fact that the data analyst can control the FWER, i.e. she can guarantee that Pr(V ≥ 1) ≤ α for any pre-specifed α, but she cannot guarantee that V = 0 on any particular dataset (short of failing to reject any null hypotheses, i.e. setting R = 0).
Therefore, we instead control the false discovery rate (FDR)15, defned false as
\[\text{FDR} = \text{E(FDP)} = \text{E(V/R)}.\tag{13.9} \stackrel{\text{discovery}}{\text{rate}}\]
When we control the FDR at (say) level q = 20%, we are rejecting as many null hypotheses as possible while guaranteeing that no more than 20% of those rejected null hypotheses are false positives, on average.
In the defnition of the FDR in (13.9), the expectation is taken over the population from which the data are generated. For instance, suppose we control the FDR for m null hypotheses at q = 0.2. This means that if we repeat this experiment a huge number of times, and each time control the FDR at q = 0.2, then we should expect that, on average, 20% of the rejected null hypotheses will be false positives. On a given dataset, the fraction of false positives among the rejected hypotheses may be greater than or less than 20%.
Thus far, we have motivated the use of the FDR from a pragmatic perspective, by arguing that when m is large, controlling the FWER is simply too stringent, and will not lead to “enough” discoveries. An additional motivation for the use of the FDR is that it aligns well with the way that data are often collected in contemporary applications. As datasets continue to grow in size across a variety of felds, it is increasingly common to conduct a huge number of hypothesis tests for exploratory, rather than confrmatory, purposes. For instance, a genomic researcher might sequence the genomes of individuals with and without some particular medical condition, and then, for each of 20,000 genes, test whether sequence variants in that gene are associated with the medical condition of interest. This amounts to performing m = 20,000 hypothesis tests. The analysis is exploratory in nature, in the sense that the researcher does not have any particular hypothesis in mind; instead she wishes to see whether there is modest evidence for the association between each gene and the disease, with a plan to further investigate any genes for which there is such evidence. She is likely willing to tolerate some number of false positives in the set of genes that she will investigate further; thus, the FWER is not an appropriate choice. However, some correction for multiple testing is required: it would not be a good idea for her to simply investigate all genes with p-values less than (say) 0.05, since we would expect 1,000 genes to have such small p-values simply by chance, even if no genes are associated with the disease (since 0.05 × 20,000 = 1,000). Controlling the FDR for her exploratory analysis at 20% guarantees that — on average — no more than 20% of the genes that she investigates further are false positives.
It is worth noting that unlike p-values, for which a threshold of 0.05 is typically viewed as the minimum standard of evidence for a “positive” result, and a threshold of 0.01 or even 0.001 is viewed as much more compelling, there is no standard accepted threshold for FDR control. Instead, the choice of FDR threshold is typically context-dependent, or even datasetdependent. For instance, the genomic researcher in the previous example might seek to control the FDR at a threshold of 10% if the planned follow-
15If R = 0, then we replace the ratio V /R with 0, to avoid computing 0/0. Formally, FDR = E(V /R|R > 0) Pr(R > 0).
up analysis is time-consuming or expensive. Alternatively, a much larger threshold of 30% might be suitable if she plans an inexpensive follow-up analysis.
13.4.2 The Benjamini–Hochberg Procedure
We now focus on the task of controlling the FDR: that is, deciding which null hypotheses to reject while guaranteeing that the FDR, E(V /R), is less than or equal to some pre-specifed value q. In order to do this, we need some way to connect the p-values, p1,…,pm, from the m null hypotheses to the desired FDR value, q. It turns out that a very simple procedure, outlined in Algorithm 13.2, can be used to control the FDR.
Algorithm 13.2 Benjamini–Hochberg Procedure to Control the FDR
- Specify q, the level at which to control the FDR.
- Compute p-values, p1,…,pm, for the m null hypotheses H01,…,H0m.
- Order the m p-values so that p(1) ≤ p(2) ≤ ··· ≤ p(m).
- Defne
\[L = \max\{j : p\_{(j)} < qj/m\}.\tag{13.10}\]
- Reject all null hypotheses H0j for which pj ≤ p(L).
Algorithm 13.2 is known as the Benjamini–Hochberg procedure. The crux Benjamini– Hochberg procedure of this procedure lies in (13.10). For example, consider again the frst fve managers in the Fund dataset, presented in Table 13.3. (In this example, m = 5, although typically we control the FDR in settings involving a much greater number of null hypotheses.) We see that p(1) = 0.006 < 0.05 × 1/5, p(2) = 0.012 < 0.05 × 2/5, p(3) = 0.601 > 0.05 × 3/5, p(4) = 0.756 > 0.05 × 4/5, and p(5) = 0.918 > 0.05 × 5/5. Therefore, to control the FDR at 5%, we reject the null hypotheses that the frst and third fund managers perform no better than chance.
As long as the m p-values are independent or only mildly dependent, then the Benjamini–Hochberg procedure guarantees16 that
\[\text{FDR} \le q.\]
In other words, this procedure ensures that, on average, no more than a fraction q of the rejected null hypotheses are false positives. Remarkably, this holds regardless of how many null hypotheses are true, and regardless of the distribution of the p-values for the null hypotheses that are false. Therefore, the Benjamini–Hochberg procedure gives us a very easy way to determine, given a set of m p-values, which null hypotheses to reject in order to control the FDR at any pre-specifed level q.
16However, the proof is well beyond the scope of this book.
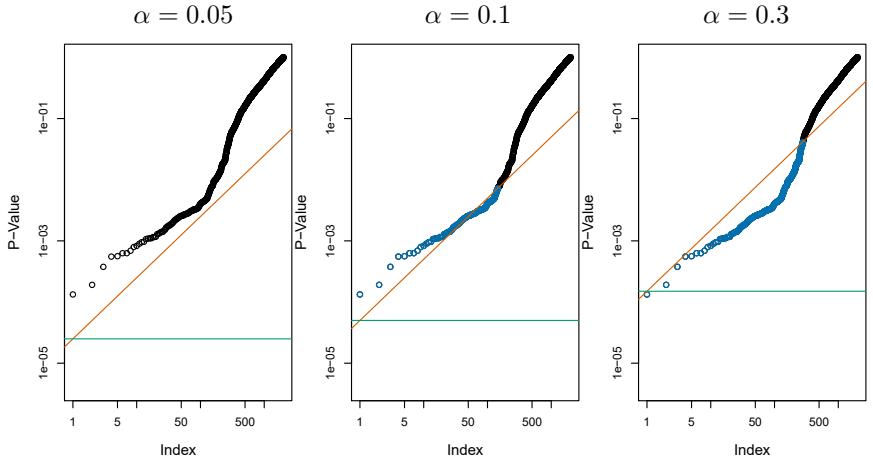
FIGURE 13.6. Each panel displays the same set of m = 2,000 ordered p-values for the Fund data. The green lines indicate the p-value thresholds corresponding to FWER control, via the Bonferroni procedure, at levels α = 0.05 (left), α = 0.1 (center), and α = 0.3 (right). The orange lines indicate the p-value thresholds corresponding to FDR control, via Benjamini–Hochberg, at levels q = 0.05 (left), q = 0.1 (center), and q = 0.3 (right). When the FDR is controlled at level q = 0.1, 146 null hypotheses are rejected (center); the corresponding p-values are shown in blue. When the FDR is controlled at level q = 0.3, 279 null hypotheses are rejected (right); the corresponding p-values are shown in blue.
There is a fundamental diference between the Bonferroni procedure of Section 13.3.2 and the Benjamini–Hochberg procedure. In the Bonferroni procedure, in order to control the FWER for m null hypotheses at level α, we must simply reject null hypotheses for which the p-value is below α/m. This threshold of α/m does not depend on anything about the data (beyond the value of m), and certainly does not depend on the p-values themselves. By contrast, the rejection threshold used in the Benjamini– Hochberg procedure is more complicated: we reject all null hypotheses for which the p-value is less than or equal to the Lth smallest p-value, where L is itself a function of all m p-values, as in (13.10). Therefore, when conducting the Benjamini–Hochberg procedure, we cannot plan out in advance what threshold we will use to reject p-values; we need to frst see our data. For instance, in the abstract, there is no way to know whether we will reject a null hypothesis corresponding to a p-value of 0.01 when using an FDR threshold of 0.1 with m = 100; the answer depends on the values of the other m − 1 p-values. This property of the Benjamini–Hochberg procedure is shared by the Holm procedure, which also involves a data-dependent p-value threshold.
Figure 13.6 displays the results of applying the Bonferroni and Benjamini– Hochberg procedures on the Fund data set, using the full set of m = 2,000 fund managers, of which the frst fve were displayed in Table 13.3. When the FWER is controlled at level 0.3 using Bonferroni, only one null hypothesis is rejected; that is, we can conclude only that a single fund manager is beating the market. This is despite the fact that a substantial portion of
the m = 2,000 fund managers appear to have beaten the market without performing correction for multiple testing — for instance, 13 of them have p-values below 0.001. By contrast, when the FDR is controlled at level 0.3, we can conclude that 279 fund managers are beating the market: we expect that no more than around 279×0.3 = 83.7 of these fund managers had good performance only due to chance. Thus, we see that FDR control is much milder — and more powerful — than FWER control, in the sense that it allows us to reject many more null hypotheses, with a cost of substantially more false positives.
The Benjamini–Hochberg procedure has been around since the mid-1990s. While a great many papers have been published since then proposing alternative approaches for FDR control that can perform better in particular scenarios, the Benjamini–Hochberg procedure remains a very useful and widely-applicable approach.
13.5 A Re-Sampling Approach to p-Values and False Discovery Rates
Thus far, the discussion in this chapter has assumed that we are interested in testing a particular null hypothesis H0 using a test statistic T, which has some known (or assumed) distribution under H0, such as a normal distribution, a t-distribution, a χ2-distribution, or an F-distribution. This is referred to as the theoretical null distribution. We typically rely upon theoretical the availability of a theoretical null distribution in order to obtain a pvalue associated with our test statistic. Indeed, for most of the types of null hypotheses that we might be interested in testing, a theoretical null distribution is available, provided that we are willing to make stringent assumptions about our data.
null distribution
However, if our null hypothesis H0 or test statistic T is somewhat unusual, then it may be the case that no theoretical null distribution is available. Alternatively, even if a theoretical null distribution exists, then we may be wary of relying upon it, perhaps because some assumption that is required for it to hold is violated. For instance, maybe the sample size is too small.
In this section, we present a framework for performing inference in this setting, which exploits the availability of fast computers in order to approximate the null distribution of T, and thereby to obtain a p-value. While this framework is very general, it must be carefully instantiated for a specifc problem of interest. Therefore, in what follows, we consider a specifc example in which we wish to test whether the means of two random variables are equal, using a two-sample t-test.
The discussion in this section is more challenging than the preceding sections in this chapter, and can be safely skipped by a reader who is content to use the theoretical null distribution to compute p-values for his or her test statistics.
13.5.1 A Re-Sampling Approach to the p-Value
We return to the example of Section 13.1.1, in which we wish to test whether the mean of a random variable X equals the mean of a random variable Y , i.e. H0 : E(X) = E(Y ), against the alternative Ha : E(X) = E( ̸ Y ). Given nX independent observations from X and nY independent observations from Y , the two-sample t-statistic takes the form
\[T = \frac{\hat{\mu}\_X - \hat{\mu}\_Y}{s\sqrt{\frac{1}{n\_X} + \frac{1}{n\_Y}}}\tag{13.11}\]
where µˆX = 1 nX #nX i=1 xi, µˆY = 1 nY #nY i=1 yi, s = L(nX−1)s2 X+(nY −1)s2 Y nX+nY −2 , and s2 X and s2 Y are unbiased estimators of the variances in the two groups. A large (absolute) value of T provides evidence against H0.
If nX and nY are large, then T in (13.11) approximately follows a N(0, 1) distribution. But if nX and nY are small, then in the absence of a strong assumption about the distribution of X and Y , we do not know the theoretical null distribution of T. 17 In this case, it turns out that we can approximate the null distribution of T using a re-sampling approach, or re-sampling more specifcally, a permutation approach. permutation To do this, we conduct a thought experiment. If H0 holds, so that E(X) =
E(Y ), and we make the stronger assumption that the distributions of X and Y are the same, then the distribution of T is invariant under swapping observations of X with observations of Y . That is, if we randomly swap some of the observations in X with the observations in Y , then the test statistic T in (13.11) computed based on this swapped data has the same distribution as T based on the original data. This is true only if H0 holds, and the distributions of X and Y are the same.
This suggests that in order to approximate the null distribution of T, we can take the following approach. We randomly permute the nX + nY observations B times, for some large value of B, and each time we compute (13.11). We let T ∗1,…,T ∗B denote the values of (13.11) on the permuted data. These can be viewed as an approximation of the null distribution of T under H0. Recall that by defnition, a p-value is the probability of observing a test statistic at least this extreme under H0. Therefore, to compute a p-value for T, we can simply compute
\[p\text{-value} = \frac{\sum\_{b=1}^{B} \mathbf{1}\_{\left( \left| T^{\*b} \right| \ge \left| T \right| \right)}}{B},\tag{13.12}\]
the fraction of permuted datasets for which the value of the test statistic is at least as extreme as the value observed on the original data. This procedure is summarized in Algorithm 13.3.
17If we assume that X and Y are normally distributed, then T in (13.11) follows a t-distribution with nX + nY − 2 degrees of freedom under H0. However, in practice, the distribution of random variables is rarely known, and so it can be preferable to perform a re-sampling approach instead of making strong and unjustifed assumptions. If the results of the re-sampling approach disagree with the results of assuming a theoretical null distribution, then the results of the re-sampling approach are more trustworthy.
Algorithm 13.3 Re-Sampling p-Value for a Two-Sample t-Test
- Compute T, defned in (13.11), on the original data x1,…,xnX and y1,…,ynY .
- For b = 1,…,B, where B is a large number (e.g. B = 10,000):
- Permute the nX + nY observations at random. Call the frst nX permuted observations x∗ 1,…,x∗ nX , and call the remaining nY observations y∗ 1,…,y∗ nY .
- Compute (13.11) on the permuted data x∗ 1,…,x∗ nX and y∗ 1,…,y∗ nY , and call the result T ∗b.
- The p-value is given by !B b=1 1(|T ∗b|≥|T |) B .
We try out this procedure on the Khan dataset, which consists of expression measurements for 2,308 genes in four sub-types of small round blood cell tumors, a type of cancer typically seen in children. This dataset is part of the ISLR2 package. We restrict our attention to the two sub-types for which the most observations are available: rhabdomyosarcoma (nX = 29) and Burkitt’s lymphoma (nY = 25).
A two-sample t-test for the null hypothesis that the 11th gene’s mean expression values are equal in the two groups yields T = −2.09. Using the theoretical null distribution, which is a t52 distribution (since nX + nY − 2 = 52), we obtain a p-value of 0.041. (Note that a t52 distribution is virtually indistinguishable from a N(0, 1) distribution.) If we instead apply Algorithm 13.3 with B = 10,000, then we obtain a p-value of 0.042. Figure 13.7 displays the theoretical null distribution, the re-sampling null distribution, and the actual value of the test statistic (T = −2.09) for this gene. In this example, we see very little diference between the p-values obtained using the theoretical null distribution and the re-sampling null distribution.
By contrast, Figure 13.8 shows an analogous set of results for the 877th gene. In this case, there is a substantial diference between the theoretical and re-sampling null distributions, which results in a diference between their p-values.
In general, in settings with a smaller sample size or a more skewed data distribution (so that the theoretical null distribution is less accurate), the diference between the re-sampling and theoretical p-values will tend to be more pronounced. In fact, the substantial diference between the resampling and theoretical null distributions in Figure 13.8 is due to the fact that a single observation in the 877th gene is very far from the other observations, leading to a very skewed distribution.
13.5.2 A Re-Sampling Approach to the False Discovery Rate
Now, suppose that we wish to control the FDR for m null hypotheses, H01,…,H0m, in a setting in which either no theoretical null distribution is available, or else we simply prefer to avoid the use of a theoretical null
FIGURE 13.7. The 11th gene in the Khan dataset has a test statistic of T = −2.09. Its theoretical and re-sampling null distributions are almost identical. The theoretical p-value equals 0.041 and the re-sampling p-value equals 0.042.
FIGURE 13.8. The 877th gene in the Khan dataset has a test statistic of T = −0.57. Its theoretical and re-sampling null distributions are quite diferent. The theoretical p-value equals 0.571, and the re-sampling p-value equals 0.673.
distribution. As in Section 13.5.1, we make use of a two-sample t-statistic for each hypothesis, leading to the test statistics T1,…,Tm. We could simply compute a p-value for each of the m null hypotheses, as in Section 13.5.1, and then apply the Benjamini–Hochberg procedure of Section 13.4.2 to these p-values. However, it turns out that we can do this in a more direct way, without even needing to compute p-values.
Recall from Section 13.4 that the FDR is defned as E(V /R), using the notation in Table 13.2. In order to estimate the FDR via re-sampling, we frst make the following approximation:
\[\text{FDR} = E\left(\frac{V}{R}\right) \approx \frac{\text{E}(V)}{R}.\tag{13.13}\]
Now suppose we reject any null hypothesis for which the test statistic exceeds c in absolute value. Then computing R in the denominator on the right-hand side of (13.13) is straightforward: R = #m j=1 1(|Tj |≥c).
However, the numerator E(V ) on the right-hand side of (13.13) is more challenging. This is the expected number of false positives associated with rejecting any null hypothesis for which the test statistic exceeds c in absolute value. At the risk of stating the obvious, estimating V is challenging because we do not know which of H01,…,H0m are really true, and so we do not know which rejected hypotheses are false positives. To overcome this problem, we take a re-sampling approach, in which we simulate data under H01,…,H0m, and then compute the resulting test statistics. The number of re-sampled test statistics that exceed c provides an estimate of V .
In greater detail, in the case of a two-sample t-statistic (13.11) for each of the null hypotheses H01,…,H0m, we can estimate E(V ) as follows. Let x(j) 1 ,…,x(j) nX and y(j) 1 ,…,y(j) nY denote the data associated with the jth null hypothesis, j = 1,…,m. We permute these nX + nY observations at random, and then compute the t-statistic on the permuted data. For this permuted data, we know that all of the null hypotheses H01,…,H0m hold; therefore, the number of permuted t-statistics that exceed the threshold c in absolute value provides an estimate for E(V ). This estimate can be further improved by repeating the permutation process B times, for a large value of B, and averaging the results.
Algorithm 13.4 details this procedure.18 It provides what is known as a plug-in estimate of the FDR, because the approximation in (13.13) allows us to estimate the FDR by plugging R into the denominator and an estimate for E(V ) into the numerator.
We apply the re-sampling approach to the FDR from Algorithm 13.4, as well as the Benjamini–Hochberg approach from Algorithm 13.2 using theoretical p-values, to the m = 2,308 genes in the Khan dataset. Results are shown in Figure 13.9. We see that for a given number of rejected hypotheses, the estimated FDRs are almost identical for the two methods.
We began this section by noting that in order to control the FDR for m hypothesis tests using a re-sampling approach, we could simply compute m re-sampling p-values as in Section 13.5.1, and then apply the Benjamini– Hochberg procedure of Section 13.4.2 to these p-values. It turns out that if we defne the jth re-sampling p-value as
\[p\_j = \frac{\sum\_{j'=1}^m \sum\_{b=1}^B \mathbf{1}\_{\left(|T\_{j'}^{\*b}| \ge |T\_j|\right)}}{Bm} \tag{13.14}\]
for j = 1,…,m, instead of as in (13.12), then applying the Benjamini– Hochberg procedure to these re-sampled p-values is exactly equivalent to Algorithm 13.4. Note that (13.14) is an alternative to (13.12) that pools the information across all m hypothesis tests in approximating the null distribution.
13.5.3 When Are Re-Sampling Approaches Useful?
In Sections 13.5.1 and 13.5.2, we considered testing null hypotheses of the form H0 : E(X) = E(Y ) using a two-sample t-statistic (13.11), for which we
18To implement Algorithm 13.4 efciently, the same set of permutations in Step 2(b)i. should be used for all m null hypotheses.
Algorithm 13.4 Plug-In FDR for a Two-Sample T-Test
- Select a threshold c, where c > 0.
- For j = 1,…,m:
- Compute T(j) , the two-sample t-statistic (13.11) for the null hypothesis H0j on the basis of the original data, x(j) 1 ,…,x(j) nX and y(j) 1 ,…,y(j) nY .
- For b = 1,…,B, where B is a large number (e.g. B = 10,000):
- Permute the nX +nY observations at random. Call the frst nX observations x∗(j) 1 ,…,x∗(j) nX , and call the remaining observations y∗(j) 1 ,…,y∗(j) nY .
- Compute (13.11) on the permuted data x∗(j) 1 ,…,x∗(j) nX and y∗(j) 1 ,…,y∗(j) nY , and call the result T(j),∗b.
- Compute R = #m j=1 1(|T(j)|≥c).
\[4.\text{ Compute }\widehat{V} = \frac{\sum\_{b=1}^{B} \sum\_{j=1}^{m} 1\_{\left(\left\lfloor T^{\left(j\right)}, \star b\right\rfloor \ge c}}}{B}.\]
- The estimated FDR associated with the threshold c is V /R I .
approximated the null distribution via a re-sampling approach. We saw that using the re-sampling approach gave us substantially diferent results from using the theoretical p-value approach in Figure 13.8, but not in Figure 13.7.
In general, there are two settings in which a re-sampling approach is particularly useful:
- Perhaps no theoretical null distribution is available. This may be the case if you are testing an unusual null hypothesis H0, or using an unsual test statistic T.
- Perhaps a theoretical null distribution is available, but the assumptions required for its validity do not hold. For instance, the twosample t-statistic in (13.11) follows a tnX+nY −2 distribution only if the observations are normally distributed. Furthermore, it follows a N(0, 1) distribution only if nX and nY are quite large. If the data are non-normal and nX and nY are small, then p-values that make use of the theoretical null distribution will not be valid (i.e. they will not properly control the Type I error).
In general, if you can come up with a way to re-sample or permute your observations in order to generate data that follow the null distribution, then you can compute p-values or estimate the FDR using variants of Algorithms 13.3 and 13.4. In many real-world settings, this provides a powerful tool for hypothesis testing when no out-of-box hypothesis tests are available, or when the key assumptions underlying those out-of-box tests are violated.
FIGURE 13.9. For j = 1,…,m = 2,308, we tested the null hypothesis that for the jth gene in the Khan dataset, the mean expression in Burkitt’s lymphoma equals the mean expression in rhabdomyosarcoma. For each value of k from 1 to 2,308, the y-axis displays the estimated FDR associated with rejecting the null hypotheses corresponding to the k smallest p-values. The orange dashed curve shows the FDR obtained using the Benjamini–Hochberg procedure, whereas the blue solid curve shows the FDR obtained using the re-sampling approach of Algorithm 13.4, with B = 10,000. There is very little diference between the two FDR estimates. According to either estimate, rejecting the null hypothesis for the 500 genes with the smallest p-values corresponds to an FDR of around 17.7%.
13.6 Lab: Multiple Testing
We include our usual imports seen in earlier labs.
In [1]: import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import statsmodels.api as sm
from ISLP import load_dataWe also collect the new imports needed for this lab.
In [2]: from scipy.stats import \
(ttest_1samp,
ttest_rel,
ttest_ind,
t as t_dbn)
from statsmodels.stats.multicomp import \
pairwise_tukeyhsd
from statsmodels.stats.multitest import \
multipletests as mult_test13.6.1 Review of Hypothesis Tests
We begin by performing some one-sample t-tests. First we create 100 variables, each consisting of 10 observations. The frst 50 variables have mean 0.5 and variance 1, while the others have mean 0 and variance 1.
In [3]: rng = np.random.default_rng(12)
X = rng.standard_normal((10, 100))
true_mean = np.array([0.5]*50 + [0]*50)
X += true_mean[None,:]584 13. Multiple Testing
To begin, we use ttest_1samp() from the scipy.stats module to test H0 : ttest_1samp() µ1 = 0, the null hypothesis that the frst variable has mean zero.
In [4]: result = ttest_1samp(X[:,0], 0)
result.pvalueOut[4]: 0.931
The p-value comes out to 0.931, which is not low enough to reject the null hypothesis at level α = 0.05. In this case, µ1 = 0.5, so the null hypothesis is false. Therefore, we have made a Type II error by failing to reject the null hypothesis when the null hypothesis is false.
We now test H0,j : µj = 0 for j = 1,…, 100. We compute the 100 pvalues, and then construct a vector recording whether the jth p-value is less than or equal to 0.05, in which case we reject H0j , or greater than 0.05, in which case we do not reject H0j , for j = 1,…, 100.
In [5]: p_values = np.empty(100)for i in range(100):
p_values[i] = ttest_1samp(X[:,i], 0).pvalue
decision = pd.cut(p_values,
[0, 0.05, 1],
labels=['Reject H0',
'Do not reject H0'])
truth = pd.Categorical(true_mean == 0,
categories=[True, False],
ordered=True)Since this is a simulated data set, we can create a 2 × 2 table similar to Table 13.2.
In [6]: pd.crosstab(decision,
truth,
rownames=['Decision'],
colnames=['H0'])| Out[6]: | H0 | True | False | |||
|---|---|---|---|---|---|---|
| Decision | ||||||
| Reject | H0 | 5 | 15 | |||
| Do | not | reject | H0 | 45 | 35 |
Therefore, at level α = 0.05, we reject 15 of the 50 false null hypotheses, and we incorrectly reject 5 of the true null hypotheses. Using the notation from Section 13.3, we have V = 5, S = 15, U = 45 and W = 35. We have set α = 0.05, which means that we expect to reject around 5% of the true null hypotheses. This is in line with the 2 × 2 table above, which indicates that we rejected V = 5 of the 50 true null hypotheses.
In the simulation above, for the false null hypotheses, the ratio of the mean to the standard deviation was only 0.5/1=0.5. This amounts to quite a weak signal, and it resulted in a high number of Type II errors. Let’s instead simulate data with a stronger signal, so that the ratio of the mean to the standard deviation for the false null hypotheses equals 1. We make only 10 Type II errors.
In [7]: true_mean = np.array([1]*50 + [0]*50)
X = rng.standard_normal((10, 100))
X += true_mean[None,:]
for i in range(100):
p_values[i] = ttest_1samp(X[:,i], 0).pvalue
decision = pd.cut(p_values,
[0, 0.05, 1],
labels=['Reject H0',
'Do not reject H0'])
truth = pd.Categorical(true_mean == 0,
categories=[True, False],
ordered=True)
pd.crosstab(decision,
truth,
rownames=['Decision'],
colnames=['H0'])| Out[7]: | H0 | True | False | |||
|---|---|---|---|---|---|---|
| Decision | ||||||
| Reject | H0 | 2 | 40 | |||
| Do | not | reject | H0 | 48 | 10 |
13.6.2 Family-Wise Error Rate
Recall from (13.5) that if the null hypothesis is true for each of m independent hypothesis tests, then the FWER is equal to 1 − (1 − α)m. We can use this expression to compute the FWER for m = 1,…, 500 and α = 0.05, 0.01, and 0.001. We plot the FWER for these values of α in order to reproduce Figure 13.2.
In [8]: m = np.linspace(1, 501)
fig, ax = plt.subplots()
[ax.plot(m,
1 - (1 - alpha)**m,
label=r'$\alpha=%s$' % str(alpha))
for alpha in [0.05, 0.01, 0.001]]
ax.set_xscale('log')
ax.set_xlabel('Number of Hypotheses')
ax.set_ylabel('Family-Wise Error Rate')
ax.legend()
ax.axhline(0.05, c='k', ls='--');As discussed previously, even for moderate values of m such as 50, the FWER exceeds 0.05 unless α is set to a very low value, such as 0.001. Of course, the problem with setting α to such a low value is that we are likely to make a number of Type II errors: in other words, our power is very low.
We now conduct a one-sample t-test for each of the frst fve managers in the Fund dataset, in order to test the null hypothesis that the jth fund manager’s mean return equals zero, H0,j : µj = 0.
In [9]: Fund = load_data('Fund')
fund_mini = Fund.iloc[:,:5]
fund_mini_pvals = np.empty(5)
for i in range(5):586 13. Multiple Testing
fund_mini_pvals[i] = ttest_1samp(fund_mini.iloc[:,i], 0).pvalue
fund_mini_pvalsOut[9]: array([0.006, 0.918, 0.012, 0.601, 0.756])
The p-values are low for Managers One and Three, and high for the other three managers. However, we cannot simply reject H0,1 and H0,3, since this would fail to account for the multiple testing that we have performed. Instead, we will conduct Bonferroni’s method and Holm’s method to control the FWER.
To do this, we use the multipletests() function from the statsmodels multiple- module (abbreviated to tests() mult_test()). Given the p-values, for methods like Holm and Bonferroni the function outputs adjusted p-values, which can be adjusted p-values thought of as a new set of p-values that have been corrected for multiple testing. If the adjusted p-value for a given hypothesis is less than or equal to α, then that hypothesis can be rejected while maintaining a FWER of no more than α. In other words, for such methods, the adjusted p-values resulting from the multipletests() function can simply be compared to the desired FWER in order to determine whether or not to reject each hypothesis. We will later see that we can use the same function to control FDR as well.
The mult_test() function takes p-values and a method argument, as well as an optional alpha argument. It returns the decisions (reject below) as well as the adjusted p-values (bonf).
In [10]: reject, bonf = mult_test(fund_mini_pvals, method = "bonferroni")[:2]
rejectOut[10]: array([ True, False, False, False, False])
The p-values bonf are simply the fund_mini_pvalues multiplied by 5 and truncated to be less than or equal to 1.
In [11]: bonf, np.minimum(fund_mini_pvals * 5, 1)
Out[11]: (array([0.03, 1. , 0.06, 1. , 1. ]),
array([0.03, 1. , 0.06, 1. , 1. ]))Therefore, using Bonferroni’s method, we are able to reject the null hypothesis only for Manager One while controlling FWER at 0.05.
By contrast, using Holm’s method, the adjusted p-values indicate that we can reject the null hypotheses for Managers One and Three at a FWER of 0.05.
In [12]: mult_test(fund_mini_pvals, method = "holm", alpha=0.05)[:2]Out[12]: (array([ True, False, True, False, False]),
array([0.03, 1. , 0.05, 1. , 1. ]))As discussed previously, Manager One seems to perform particularly well, whereas Manager Two has poor performance.
In [13]: fund_mini.mean()Out[13]: Manager1 3.0
Manager2 -0.1
Manager3 2.8
Manager4 0.5
Manager5 0.3
dtype: float64Is there evidence of a meaningful diference in performance between these two managers? We can check this by performing a paired t-test using the paired t-test ttest_rel() function from scipy.stats: ttest_rel()
In [14]: ttest_rel(fund_mini['Manager1'],
fund_mini['Manager2']).pvalueOut[14]: 0.038
The test results in a p-value of 0.038, suggesting a statistically signifcant diference.
However, we decided to perform this test only after examining the data and noting that Managers One and Two had the highest and lowest mean performances. In a sense, this means that we have implicitly performed 55 2 6 = 5(5 − 1)/2 = 10 hypothesis tests, rather than just one, as discussed in Section 13.3.2. Hence, we use the pairwise_tukeyhsd() function from pairwise_ tukeyhsd() statsmodels.stats.multicomp to apply Tukey’s method in order to adjust for multiple testing. This function takes as input a ftted ANOVA regres- ANOVA sion model, which is essentially just a linear regression in which all of the predictors are qualitative. In this case, the response consists of the monthly excess returns achieved by each manager, and the predictor indicates the manager to which each return corresponds.
In [15]: returns = np.hstack([fund_mini.iloc[:,i] for i in range(5)])
managers = np.hstack([[i+1]*50 for i in range(5)])
tukey = pairwise_tukeyhsd(returns, managers)
print(tukey.summary())Multiple Comparison of Means - Tukey HSD, FWER=0.05
===================================================
group1 group2 meandiff p-adj lower upper reject
---------------------------------------------------
1 2 -3.1 0.1862 -6.9865 0.7865 False
1 3 -0.2 0.9999 -4.0865 3.6865 False
1 4 -2.5 0.3948 -6.3865 1.3865 False
1 5 -2.7 0.3152 -6.5865 1.1865 False
2 3 2.9 0.2453 -0.9865 6.7865 False
2 4 0.6 0.9932 -3.2865 4.4865 False
2 5 0.4 0.9986 -3.4865 4.2865 False
3 4 -2.3 0.482 -6.1865 1.5865 False
3 5 -2.5 0.3948 -6.3865 1.3865 False
4 5 -0.2 0.9999 -4.0865 3.6865 False
---------------------------------------------------The pairwise_tukeyhsd() function provides confdence intervals for the diference between each pair of managers (lower and upper), as well as a
FIGURE 13.10. 95% confdence intervals for each manager on the Fund data, using Tukey’s method to adjust for multiple testing. All of the confdence intervals overlap, so none of the diferences among managers are statistically signifcant when controlling FWER at level 0.05.
p-value. All of these quantities have been adjusted for multiple testing. Notice that the p-value for the diference between Managers One and Two has increased from 0.038 to 0.186, so there is no longer clear evidence of a diference between the managers’ performances. We can plot the confdence intervals for the pairwise comparisons using the plot_simultaneous() method of tukey. Any pair of intervals that don’t overlap indicates a signifcant diference at the nominal level of 0.05. In this case, no diferences are considered signifcant as reported in the table above.
In [16]: fig, ax = plt.subplots(figsize=(8,8))
tukey.plot_simultaneous(ax=ax);13.6.3 False Discovery Rate
Now we perform hypothesis tests for all 2,000 fund managers in the Fund dataset. We perform a one-sample t-test of H0,j : µj = 0, which states that the jth fund manager’s mean return is zero.
In [17]: fund_pvalues = np.empty(2000)
for i, manager in enumerate(Fund.columns):
fund_pvalues[i] = ttest_1samp(Fund[manager], 0).pvalueThere are far too many managers to consider trying to control the FWER. Instead, we focus on controlling the FDR: that is, the expected fraction of rejected null hypotheses that are actually false positives. The
19Traditionally this plot shows intervals for each paired diference. With many groups it is more convenient and equivalent to display one interval per group, as is done here. By “diferencing” all pairs of intervals displayed here you recover the traditional plot.
multipletests() function (abbreviated mult_test()) can be used to carry out the Benjamini–Hochberg procedure.
In [18]: fund_qvalues = mult_test(fund_pvalues, method = "fdr_bh")[1]
fund_qvalues[:10]Out[18]: array([0.09, 0.99, 0.12, 0.92, 0.96, 0.08, 0.08, 0.08, 0.08,
0.08])The q-values output by the Benjamini–Hochberg procedure can be inter- q-values preted as the smallest FDR threshold at which we would reject a particular null hypothesis. For instance, a q-value of 0.1 indicates that we can reject the corresponding null hypothesis at an FDR of 10% or greater, but that we cannot reject the null hypothesis at an FDR below 10%.
If we control the FDR at 10%, then for how many of the fund managers can we reject H0,j : µj = 0?
In [19]: (fund_qvalues <= 0.1).sum()
Out[19]: 146
We fnd that 146 of the 2,000 fund managers have a q-value below 0.1; therefore, we are able to conclude that 146 of the fund managers beat the market at an FDR of 10%. Only about 15 (10% of 146) of these fund managers are likely to be false discoveries.
By contrast, if we had instead used Bonferroni’s method to control the FWER at level α = 0.1, then we would have failed to reject any null hypotheses!
In [20]: (fund_pvalues <= 0.1 / 2000).sum()
Out[20]: 0
Figure 13.6 displays the ordered p-values, p(1) ≤ p(2) ≤ ··· ≤ p(2000), for the Fund dataset, as well as the threshold for rejection by the Benjamini– Hochberg procedure. Recall that the Benjamini–Hochberg procedure identifes the largest p-value such that p(j) < qj/m, and rejects all hypotheses for which the p-value is less than or equal to p(j). In the code below, we implement the Benjamini–Hochberg procedure ourselves, in order to illustrate how it works. We frst order the p-values. We then identify all p-values that satisfy p(j) < qj/m (sorted_set_). Finally, selected_ is a boolean array indicating which p-values are less than or equal to the largest p-value in sorted_[sorted_set_]. Therefore, selected_ indexes the p-values rejected by the Benjamini–Hochberg procedure.
In [21]: sorted_ = np.sort(fund_pvalues)
m = fund_pvalues.shape[0]
q = 0.1
sorted_set_ = np.where(sorted_ < q * np.linspace(1, m, m) / m)[0]
if sorted_set_.shape[0] > 0:
selected_ = fund_pvalues < sorted_[sorted_set_].max()
sorted_set_ = np.arange(sorted_set_.max())
else:
selected_ = []
sorted_set_ = []590 13. Multiple Testing
We now reproduce the middle panel of Figure 13.6.
In [22]: fig, ax = plt.subplots()
ax.scatter(np.arange(0, sorted_.shape[0]) + 1,
sorted_, s=10)
ax.set_yscale('log')
ax.set_xscale('log')
ax.set_ylabel('P-Value')
ax.set_xlabel('Index')
ax.scatter(sorted_set_+1, sorted_[sorted_set_], c='r', s=20)
ax.axline((0, 0), (1,q/m), c='k', ls='--', linewidth=3);13.6.4 A Re-Sampling Approach
Here, we implement the re-sampling approach to hypothesis testing using the Khan dataset, which we investigated in Section 13.5. First, we merge the training and testing data, which results in observations on 83 patients for 2,308 genes.
In [23]: Khan = load_data('Khan')
D = pd.concat([Khan['xtrain'], Khan['xtest']])
D['Y'] = pd.concat([Khan['ytrain'], Khan['ytest']])
D['Y'].value_counts()Out[23]: 2 29
4 25
3 18
1 11
Name: Y, dtype: int64There are four classes of cancer. For each gene, we compare the mean expression in the second class (rhabdomyosarcoma) to the mean expression in the fourth class (Burkitt’s lymphoma). Performing a standard two-sample t-test using ttest_ind() from scipy.stats on the 11th gene produces a ttest_ind() test-statistic of -2.09 and an associated p-value of 0.0412, suggesting modest evidence of a diference in mean expression levels between the two cancer types.
In [24]: D2 = D[lambda df:df['Y'] == 2]
D4 = D[lambda df:df['Y'] == 4]
gene_11 = 'G0011'
observedT, pvalue = ttest_ind(D2[gene_11],
D4[gene_11],
equal_var=True)
observedT, pvalueOut[24]: (-2.094, 0.041)
However, this p-value relies on the assumption that under the null hypothesis of no diference between the two groups, the test statistic follows a t-distribution with 29 + 25 − 2 = 52 degrees of freedom. Instead of using this theoretical null distribution, we can randomly split the 54 patients into two groups of 29 and 25, and compute a new test statistic. Under the null hypothesis of no diference between the groups, this new test statistic should have the same distribution as our original one. Repeating this process 10,000 times allows us to approximate the null distribution of the test statistic. We compute the fraction of the time that our observed test statistic exceeds the test statistics obtained via re-sampling.
In [25]: B = 10000
Tnull = np.empty(B)
D_ = np.hstack([D2[gene_11], D4[gene_11]])
n_ = D2[gene_11].shape[0]
D_null = D_.copy()
for b in range(B):
rng.shuffle(D_null)
ttest_ = ttest_ind(D_null[:n_],
D_null[n_:],
equal_var=True)
Tnull[b] = ttest_.statistic
(np.abs(Tnull) > np.abs(observedT)).mean()Out[25]: 0.0398
This fraction, 0.0398, is our re-sampling-based p-value. It is almost identical to the p-value of 0.0412 obtained using the theoretical null distribution. We can plot a histogram of the re-sampling-based test statistics in order to reproduce Figure 13.7.
In [26]: fig, ax = plt.subplots(figsize=(8,8))
ax.hist(Tnull,
bins=100,
density=True,
facecolor='y',
label='Null')
xval = np.linspace(-4.2, 4.2, 1001)
ax.plot(xval,
t_dbn.pdf(xval, D_.shape[0]-2),
c='r')
ax.axvline(observedT,
c='b',
label='Observed')
ax.legend()
ax.set_xlabel("Null Distribution of Test Statistic");The re-sampling-based null distribution is almost identical to the theoretical null distribution, which is displayed in red.
Finally, we implement the plug-in re-sampling FDR approach outlined in Algorithm 13.4. Depending on the speed of your computer, calculating the FDR for all 2,308 genes in the Khan dataset may take a while. Hence, we will illustrate the approach on a random subset of 100 genes. For each gene, we frst compute the observed test statistic, and then produce 10,000 re-sampled test statistics. This may take a few minutes to run. If you are in a rush, then you could set B equal to a smaller value (e.g. B=500).
In [27]: m, B = 100, 10000idx = rng.choice(Khan['xtest'].columns, m, replace=False)
T_vals = np.empty(m)
Tnull_vals = np.empty((m, B))
for j in range(m):
col = idx[j]592 13. Multiple Testing
T_vals[j] = ttest_ind(D2[col],
D4[col],
equal_var=True).statistic
D_ = np.hstack([D2[col], D4[col]])
D_null = D_.copy()
for b in range(B):
rng.shuffle(D_null)
ttest_ = ttest_ind(D_null[:n_],
D_null[n_:],
equal_var=True)
Tnull_vals[j,b] = ttest_.statisticNext, we compute the number of rejected null hypotheses R, the estimated number of false positives VI, and the estimated FDR, for a range of threshold values c in Algorithm 13.4. The threshold values are chosen using the absolute values of the test statistics from the 100 genes.
In [28]: cutoffs = np.sort(np.abs(T_vals))
FDRs, Rs, Vs = np.empty((3, m))
for j in range(m):
R = np.sum(np.abs(T_vals) >= cutoffs[j])
V = np.sum(np.abs(Tnull_vals) >= cutoffs[j]) / B
Rs[j] = R
Vs[j] = V
FDRs[j] = V / RNow, for any given FDR, we can fnd the genes that will be rejected. For example, with FDR controlled at 0.1, we reject 15 of the 100 null hypotheses. On average, we would expect about one or two of these genes (i.e. 10% of 15) to be false discoveries. At an FDR of 0.2, we can reject the null hypothesis for 28 genes, of which we expect around six to be false discoveries.
The variable idx stores which genes were included in our 100 randomlyselected genes. Let’s look at the genes whose estimated FDR is less than 0.1.
In [29]: sorted(idx[np.abs(T_vals) >= cutoffs[FDRs < 0.1].min()])At an FDR threshold of 0.2, more genes are selected, at the cost of having a higher expected proportion of false discoveries.
In [30]: sorted(idx[np.abs(T_vals) >= cutoffs[FDRs < 0.2].min()])
The next line generates Figure 13.11, which is similar to Figure 13.9, except that it is based on only a subset of the genes.
In [31]: fig, ax = plt.subplots()
ax.plot(Rs, FDRs, 'b', linewidth=3)
ax.set_xlabel("Number of Rejections")
ax.set_ylabel("False Discovery Rate");
FIGURE 13.11. The estimated false discovery rate versus the number of rejected null hypotheses, for 100 genes randomly selected from the Khan dataset.
13.7 Exercises
Conceptual
- Suppose we test m null hypotheses, all of which are true. We control the Type I error for each null hypothesis at level α. For each subproblem, justify your answer.
- In total, how many Type I errors do we expect to make?
- Suppose that the m tests that we perform are independent. What is the family-wise error rate associated with these m tests? Hint: If two events A and B are independent, then Pr(A ∩ B) = Pr(A) Pr(B).
- Suppose that m = 2, and that the p-values for the two tests are positively correlated, so that if one is small then the other will tend to be small as well, and if one is large then the other will tend to be large. How does the family-wise error rate associated with these m = 2 tests qualitatively compare to the answer in (b) with m = 2?
Hint: First, suppose that the two p-values are perfectly correlated.
- Suppose again that m = 2, but that now the p-values for the two tests are negatively correlated, so that if one is large then the other will tend to be small. How does the family-wise error rate associated with these m = 2 tests qualitatively compare to the answer in (b) with m = 2?
Hint: First, suppose that whenever one p-value is less than α, then the other will be greater than α. In other words, we can never reject both null hypotheses.
- Suppose that we test m hypotheses, and control the Type I error for each hypothesis at level α. Assume that all m p-values are independent, and that all null hypotheses are true.
- Let the random variable Aj equal 1 if the jth null hypothesis is rejected, and 0 otherwise. What is the distribution of Aj ?
- What is the distribution of #m j=1 Aj ?
- What is the standard deviation of the number of Type I errors that we will make?
- Suppose we test m null hypotheses, and control the Type I error for the jth null hypothesis at level αj , for j = 1,…,m. Argue that the family-wise error rate is no greater than #m j=1 αj .
| Null Hypothesis | p-value |
|---|---|
| H01 | 0.0011 |
| H02 | 0.031 |
| H03 | 0.017 |
| H04 | 0.32 |
| H05 | 0.11 |
| H06 | 0.90 |
| H07 | 0.07 |
| H08 | 0.006 |
| H09 | 0.004 |
| H10 | 0.0009 |
TABLE 13.4. p-values for Exercise 4.
- Suppose we test m = 10 hypotheses, and obtain the p-values shown in Table 13.4.
- Suppose that we wish to control the Type I error for each null hypothesis at level α = 0.05. Which null hypotheses will we reject?
- Now suppose that we wish to control the FWER at level α = 0.05. Which null hypotheses will we reject? Justify your answer.
- Now suppose that we wish to control the FDR at level q = 0.05. Which null hypotheses will we reject? Justify your answer.
- Now suppose that we wish to control the FDR at level q = 0.2. Which null hypotheses will we reject? Justify your answer.
- Of the null hypotheses rejected at FDR level q = 0.2, approximately how many are false positives? Justify your answer.
- For this problem, you will make up p-values that lead to a certain number of rejections using the Bonferroni and Holm procedures.
- Give an example of fve p-values (i.e. fve numbers between 0 and 1 which, for the purpose of this problem, we will interpret as pvalues) for which both Bonferroni’s method and Holm’s method
reject exactly one null hypothesis when controlling the FWER at level 0.1.
- Now give an example of fve p-values for which Bonferroni rejects one null hypothesis and Holm rejects more than one null hypothesis at level 0.1.
- For each of the three panels in Figure 13.3, answer the following questions:
- How many false positives, false negatives, true positives, true negatives, Type I errors, and Type II errors result from applying the Bonferroni procedure to control the FWER at level α = 0.05?
- How many false positives, false negatives, true positives, true negatives, Type I errors, and Type II errors result from applying the Holm procedure to control the FWER at level α = 0.05?
- What is the false discovery proportion associated with using the Bonferroni procedure to control the FWER at level α = 0.05?
- What is the false discovery proportion associated with using the Holm procedure to control the FWER at level α = 0.05?
- How would the answers to (a) and (c) change if we instead used the Bonferroni procedure to control the FWER at level α = 0.001?
Applied
- This problem makes use of the Carseats dataset in the ISLP package.
- For each quantitative variable in the dataset besides Sales, ft a linear model to predict Sales using that quantitative variable. Report the p-values associated with the coefcients for the variables. That is, for each model of the form Y = β0 + β1X + ϵ, report the p-value associated with the coefcient β1. Here, Y represents Sales and X represents one of the other quantitative variables.
- Suppose we control the Type I error at level α = 0.05 for the p-values obtained in (a). Which null hypotheses do we reject?
- Now suppose we control the FWER at level 0.05 for the p-values. Which null hypotheses do we reject?
- Finally, suppose we control the FDR at level 0.2 for the p-values. Which null hypotheses do we reject?
- In this problem, we will simulate data from m = 100 fund managers.
rng = np.random.default_rng(1)
n, m = 20, 100
X = rng.normal(size=(n, m))These data represent each fund manager’s percentage returns for each of n = 20 months. We wish to test the null hypothesis that each fund manager’s percentage returns have population mean equal to zero. Notice that we simulated the data in such a way that each fund manager’s percentage returns do have population mean zero; in other words, all m null hypotheses are true.
- Conduct a one-sample t-test for each fund manager, and plot a histogram of the p-values obtained.
- If we control Type I error for each null hypothesis at level α = 0.05, then how many null hypotheses do we reject?
- If we control the FWER at level 0.05, then how many null hypotheses do we reject?
- If we control the FDR at level 0.05, then how many null hypotheses do we reject?
- Now suppose we “cherry-pick” the 10 fund managers who perform the best in our data. If we control the FWER for just these 10 fund managers at level 0.05, then how many null hypotheses do we reject? If we control the FDR for just these 10 fund managers at level 0.05, then how many null hypotheses do we reject?
- Explain why the analysis in (e) is misleading. Hint: The standard approaches for controlling the FWER and FDR assume that all tested null hypotheses are adjusted for multiplicity, and that no “cherry-picking” of the smallest p-values has occurred. What goes wrong if we cherry-pick?
Index
accuracy, 415 activation, 400 activation function, 401 additive, 11, 94–98, 110–111 additivity, 305, 306 adjusted R2, 87, 231, 232, 236– 238 Advertising data set, 15, 16, 19, 69, 71–73, 77, 78, 80, 82, 83, 85, 87–90, 95, 96, 109– 111 agglomerative clustering, 525 Akaike information criterion, 87, 231, 232, 236–238 alternative hypothesis, 76, 559 analysis of variance, 312 ANOVA, 587 area under the curve, 155, 486– 487 argument, 40 array, 42 attribute, 42 AUC, 155 Auto data set, 12, 66, 98–101, 129, 197, 202–207, 327, 398 auto-correlation, 421 autoregression, 423 axes, 48
backpropagation, 429 backward stepwise selection, 87, 234–235 bag-of-n-grams, 415 bag-of-words, 414 bagging, 11, 24, 331, 343–346, 354, 360–361 BART, 343, 350, 353, 354, 362– 363 baseline, 93, 145, 161 basis function, 293–294, 296 Bayes classifer, 35–37, 147 decision boundary, 148 error, 35–37 Bayes’ theorem, 146, 250 Bayesian, 250–251, 353 Bayesian additive regression trees, 331, 343, 350, 350, 353, 354, 362–363 Bayesian information criterion, 87, 231, 232, 236–238 Benjamini–Hochberg procedure, 575– 577 Bernoulli distribution, 172 best subset selection, 231, 246 bias, 31–34, 74, 90, 159, 405 bias-variance decomposition, 32
© Springer Nature Switzerland AG 2023
G. James et al., An Introduction to Statistical Learning, Springer Texts in Statistics, https://doi.org/10.1007/978-3-031-38747-0
trade-of, 31–34, 38, 111–112, 157, 159, 163, 164, 242, 254, 263, 266, 301, 336, 376, 385 bidirectional, 425 Bikeshare data set, 12, 167–172 binary, 27, 138 biplot, 507, 508 Bonferroni method, 575–577, 585 Boolean, 53, 176 boosting, 11, 24, 331, 343, 347– 350, 354, 361–362 bootstrap, 11, 201, 212–214, 343 Boston data set, 12, 67, 117, 122, 133, 199, 227, 287, 327, 364, 556 bottom-up clustering, 525 boxplot, 62 BrainCancer data set, 12, 472– 474, 476, 482 branch, 333 burn-in, 352
C-index, 487 Caravan data set, 12, 184, 366 Carseats data set, 12, 126, 130, 364 categorical, 2, 27 censored data, 469–502 censoring independent, 471 interval, 471 left, 471 mechanism, 471 non-informative, 471 right, 471 time, 470 chain rule, 429 channel, 407 CIFAR100 data set, 406, 409–411, 448, 449 classifcation, 2, 11, 27, 34–39, 135– 199, 367–382 error rate, 338 tree, 337–341, 355–358 classifer, 135 cluster analysis, 25–26 clustering, 4, 25–26, 520–535 agglomerative, 525
bottom-up, 525 hierarchical, 521, 525–535 K-means, 11, 521–524 Cochran–Mantel–Haenszel test, 475 coefcient, 71 College data set, 12, 65, 286, 328 collinearity, 106–110 concatenation, 41 conditional probability, 35 confdence interval, 75–76, 90, 110, 292 confounding, 144 confusion matrix, 153, 176 continuous, 2 contour, 246 contour plot, 50 contrast, 94 convenience function, 53 convolution flter, 407 convolution layer, 407 convolutional neural network, 406– 413 correlation, 79, 82–83, 530 count data, 167, 170 Cox’s proportional hazards model, 480, 483–486 Cp, 87, 231, 232, 236–238 Credit data set, 12, 91, 92, 94, 97, 98, 106–109 cross-entropy, 405 cross-validation, 11, 31, 34, 201– 211, 231, 252, 270 k-fold, 206–209 leave-one-out, 204–206 curse of dimensionality, 115, 193, 266
data augmentation, 411 data frame, 55 Data sets Advertising, 15, 16, 19, 69, 71–73, 77, 78, 80, 82, 83, 85, 87–90, 95, 96, 109– 111 Auto, 12, 66, 98–101, 129, 197, 202–207, 327, 398 Bikeshare, 12, 167–172
Boston, 12, 67, 117, 122, 133, 199, 227, 287, 327, 364, 556 BrainCancer, 12, 472–474, 476, 482 Caravan, 12, 184, 366 Carseats, 12, 126, 130, 364 CIFAR100, 406, 409–411, 448, 449 College, 12, 65, 286, 328 Credit, 12, 91, 92, 94, 97, 98, 106–109 Default, 12, 136–139, 141– 144, 152–156, 160, 161, 225, 226, 466 Fund, 12, 567–570, 572, 575, 576, 585, 588, 589 Heart, 339, 340, 344–347, 352, 353, 382, 383 Hitters, 12, 332, 333, 336, 338, 339, 366, 425, 426, 437, 446 IMDb, 413, 415, 416, 418, 420, 437, 458, 467 Income, 16–18, 21–23 Khan, 12, 579–581, 583, 590, 593 MNIST, 402–404, 406, 430, 431, 441, 444, 445, 448 NCI60, 4, 5, 12, 546, 548–550 NYSE, 12, 422–424, 466, 467 OJ, 12, 365, 398 Portfolio, 12 Publication, 12, 482–487 Smarket, 2, 3, 12, 173, 184, 196 USArrests, 12, 507, 508, 510, 512, 513, 515, 516, 518, 519 Wage, 1, 2, 8, 9, 12, 290, 291, 293, 295, 297–300, 302– 306, 309, 315, 327 Weekly, 12, 196, 226 data type, 42 decision function, 387 decision tree, 11, 331–342 deep learning, 399
Default data set, 12, 136–139, 141– 144, 152–156, 160, 161, 225, 226, 466 degrees of freedom, 30, 266, 295, 296, 301 dendrogram, 521, 525–530 density function, 146 dependent variable, 15 derivative, 296, 300 detector layer, 410 deviance, 232 dictionary, 66 dimension reduction, 230, 253–262 discriminant function, 149 discriminant method, 146–161 dissimilarity, 530–532 distance correlation-based, 530–532, 554 Euclidean, 509, 522, 523, 529– 532 double descent, 431–435 double-exponential distribution, 251 dropout, 406, 431 dummy variable, 91–94, 138, 142, 292 early stopping, 430 efective degrees of freedom, 301 eigen decomposition, 506, 516 elbow, 548 embedding, 418 embedding layer, 419 ensemble, 343–354 entropy, 337–339, 363 epochs, 430 error irreducible, 17, 30 rate, 34 reducible, 17 term, 16 Euclidean distance, 509, 522, 523, 529–532, 554 event time, 470 exception, 45 expected value, 18 exploratory data analysis, 504 exponential, 173 exponential family, 173 F-statistic, 84
factor, 92 factorial, 170 failure time, 470 false discovery proportion, 155, 573 discovery rate, 558, 573–577, 579–582 negative, 155, 562 positive, 155, 562, 563 positive rate, 155, 156, 382 family-wise error rate, 565–573, 577 feature, 15 feature map, 406 feature selection, 230 featurize, 414 feed-forward neural network, 400 fgure, 48 ft, 21 ftted value, 101 fattening, 424 fexible, 21 foating point, 43 forward stepwise selection, 86, 87, 233–234, 268 function, 40 Fund data set, 12, 567–570, 572, 575, 576, 585, 588, 589 Gamma, 173 Gaussian (normal) distribution, 146, 147, 150, 172, 561 generalized additive model, 5, 24, 162, 289, 290, 305–309, 319 generalized linear model, 5, 135, 167–174, 217 generative model, 146–161 Gini index, 337–339, 345, 346, 363 global minimum, 427 gradient, 428 gradient descent, 427 Harrell’s concordance index, 487 hazard function, 476–478 baseline, 478 hazard rate, 476 Heart data set, 339, 340, 344–347, 352, 353, 382, 383 heatmap, 50 helper, 311
heteroscedasticity, 103, 168 hidden layer, 400 hidden units, 400 hierarchical clustering, 525–530 dendrogram, 525–528 inversion, 529 linkage, 529–530 hierarchical principle, 96 high-dimensional, 86, 234, 263 hinge loss, 385 Hitters data set, 12, 332, 333, 336, 338, 339, 366, 425, 426, 437, 446 hold-out set, 202 Holm’s method, 568, 576, 585 hypergeometric distribution, 501 hyperparameter, 187 hyperplane, 367–372 hypothesis test, 76–77, 84, 103, 558–583
IMDb data set, 413, 415, 416, 418, 420, 437, 458, 467 imputation, 515 Income data set, 16–18, 21–23 increment, 60 independent variable, 15 indexable, 186 indicator function, 292 inference, 17, 18 inner product, 379, 380 input layer, 400 input variable, 15 integral, 301 interaction, 70, 89, 95–98, 110– 111, 308 intercept, 71, 72 interpolate, 432 interpretability, 229 inversion, 529 irreducible error, 17, 36, 90, 110 iterator, 312
joint distribution, 158
K-means clustering, 11, 521–524 K-nearest neighbors, 135, 164–167 classifer, 11, 36–37 regression, 111–115
Kaplan–Meier survival curve, 472– 474, 483 kernel, 379–382, 384, 394 linear, 380 non-linear, 377–382 polynomial, 380, 382 radial, 381–383, 390 kernel density estimator, 159 keyword, 46 Khan data set, 12, 579–581, 583, 590, 593 knot, 290, 294, 296–299 ℓ1 norm, 244 ℓ2 norm, 242 lag, 422 Laplace distribution, 251 lasso, 11, 24, 244–251, 265–266, 336, 385, 484 leaf, 333, 526 learning rate, 429 least squares, 5, 21, 71–72, 140, 141, 229 line, 73 weighted, 103 level, 92 leverage, 104–106 likelihood function, 141 linear, 2, 69–115 linear combination, 128, 230, 253, 505 linear discriminant analysis, 5, 11, 135, 138, 147–155, 164– 167, 377, 382 linear kernel, 380 linear model, 20, 69–115 linear regression, 5, 11, 69–115, 172–173 multiple, 80–90 simple, 70–80 link function, 172, 173 linkage, 529–530, 548 average, 529–530 centroid, 529–530 complete, 526, 529–530 single, 529–530 list, 41 list comprehension, 123 local minimum, 427
local regression, 290 log odds, 145 log-rank test, 474–476, 483 logistic function, 139 logistic regression, 5, 11, 25, 135, 138–144, 164–167, 172– 173, 308–309, 377, 384– 385 multinomial, 145, 163 multiple, 142–144 logit, 140 loss function, 300, 385 low-dimensional, 262 LSTM RNN, 420 main efects, 96 majority vote, 344 Mallow’s Cp, 87, 231, 232, 236– 238 Mantel–Haenszel test, 475 margin, 370, 385 marginal distribution, 158 Markov chain Monte Carlo, 353 matrix completion, 515 matrix multiplication, 10 maximal margin classifer, 367–372 hyperplane, 370 maximum likelihood, 139–141, 143, 170 mean squared error, 28 mesh, 53 method, 43 minibatch, 429 misclassifcation error, 35 missing at random, 515 missing data, 56, 515–520 mixed selection, 87 MNIST data set, 402–404, 406, 430, 431, 441, 444, 445, 448 model assessment, 201 model selection, 201 module, 42 multicollinearity, 108, 266 multinomial logistic regression, 145, 163 multiple testing, 557–583 multi-task learning, 403 multivariate Gaussian, 150
multivariate normal, 150 naive Bayes, 135, 158–161, 164– 167 namespace, 116 natural spline, 297, 298, 301, 317 NCI60 data set, 4, 5, 12, 546, 548– 550 negative binomial, 173 negative predictive value, 155, 156 neural network, 5, 399 node internal, 333 purity, 337–339 terminal, 333 noise, 21, 252 non-linear, 2, 11, 289–329 decision boundary, 377–382 kernel, 377–382 non-parametric, 20, 22–23, 111– 115, 193 normal (Gaussian) distribution, 146, 147, 150, 172, 476, 561 notebook, 40 null, 152 distribution, 561, 578 hypothesis, 76, 559 model, 87, 231, 245 null rate, 186 NYSE data set, 12, 422–424, 466, 467 Occam’s razor, 426 odds, 140, 145, 195 OJ data set, 12, 365, 398 one-hot encoding, 92, 126, 403 one-standard-error rule, 240 one-versus-all, 384 one-versus-one, 384 one-versus-rest, 384 optimal separating hyperplane, 370 optimism of training error, 30 ordered categorical variable, 315 orthogonal, 257, 506 basis, 125 out-of-bag, 345 outlier, 103–104 output variable, 15 over-parametrized, 465 overdispersion, 172
overftting, 21, 23, 25, 30–31, 88, 152, 233, 371 p-value, 77, 82, 560–562, 578–579 adjusted, 586 package, 42 parameter, 71 parametric, 20–22, 111–115 partial least squares, 254, 260–262, 282 partial likelihood, 480 path algorithm, 249 permutation, 578 permutation approach, 577–582 perpendicular, 257 Poisson distribution, 169, 172 Poisson regression, 135, 167–173 polynomial kernel, 380, 382 regression, 98–99, 289–292, 294– 295 pooling, 410 population regression line, 73 Portfolio data set, 12 positive predictive value, 155, 156 posterior distribution, 251 mode, 251 probability, 147 power, 108, 155, 563 precision, 155 prediction, 17 interval, 90, 110 predictor, 15 principal components, 505 analysis, 11, 254–260, 504–515 loading vector, 505, 506 missing values, 515–520 proportion of variance explained, 510–515, 547 regression, 11, 254–260, 280– 282, 504, 515 score vector, 506 scree plot, 514–515 prior distribution, 251 probability, 146 probability density function, 477, 478
projection, 230 proportional hazards assumption, 478 pruning, 336 cost complexity, 336 weakest link, 336 Publication data set, 12, 482– 487 Python objects and functions %%capture, 458 iloc[], 58 loc[], 57 AgglomerativeClustering(), 543 anova(), 313 anova_lm(), 125, 129, 312, 313 axhline(), 122, 551 axline(), 121, 129, 329 BART(), 362 biplot, 537 boot_SE(), 223 boxplot(), 62, 66 bs(), 315, 327 BSpline(), 315 clone(), 222 columns.drop(), 122 compute_linkage(), 544 confusion_table(), 176 contour(), 50 corr(), 129, 174 cost_complexity_pruning_path(), 357 CoxPHFitter(), 491 cross_val_predict(), 270 cross_validate(), 218, 219, 226 cumsum(), 539 cut_tree(), 545 data.frame(), 227 Dataset, 440 decision_function(), 392 DecisionTreeClassifier(), 354, 355 DecisionTreeRegressor(), 354 def, 121 dendrogram(), 544 describe(), 62, 66 dir(), 116
drop(), 179 dropna(), 56, 268, 461 DTC(), see DecisionTreeClassifier() DTR(), see DecisionTreeRegressor() dtype, 43 ElasticNetCV(), 279 enumerate(), 217 export_text(), 356 export_tree(), 365 fit(), 118, 181, 218 fit_transform(), 119 for, 59 GaussianNB(), 182 GBR(), see GradientBoosting-Regressor() get_dummies(), 461 get_influence(), 121 get_prediction(), 120, 314 get_rdataset(), 535 glm(), 313 glob(), 437 GradientBoostingClassifier(), 361 GradientBoostingRegressor(), 354, 361 GridSearchCV(), 276 groupby(), 490 hist(), 62 iloc[], 58, 59 import, 42 imshow(), 50, 449 ISLP.bart, 362 ISLP.cluster, 544 json, 437 KaplanMeierFitter(), 502 keras, 437 KFold(), 219 KMeans(), 542, 543 Kmeans(), 542 KNeighborsClassifier(), 183 lambda, 58 LDA(), see LinearDiscriminant-Analysis() legend(), 132 lifelines, 490 LinearDiscriminantAnalysis(), 174, 179 LinearGAM(), 317 LinearRegression(), 280
load_data(), 117
loc[], 58, 59, 177
log_loss(), 355
LogisticGAM(), 323
logrank_test(), 490
lowess(), 324
matplotlib, 48
max(), 66
mean(), 48
median(), 197
min(), 66
MNIST(), 444
ModelSpec(), 116–118, 122,
124, 267
MS(), see ModelSpec()
mult_test(), see multipletests()
multipletests(), 586
multipletests(), 583, 589
multivariate_logrank_test(),
496
NaturalSpline(), 317, 319
ndim, 42
nn.RNN(), 461
normal(), 132, 286, 555
np, see numpy
np.all(), 54, 180
np.allclose(), 190
np.any(), 54
np.arange(), 51
np.argmax(), 122
np.array(), 42
np.concatenate(), 133
np.corrcoef(), 46, 554
np.empty(), 224
np.isnan(), 268
np.ix_(), 53
np.linalg.svd(), 539
np.linspace(), 50
np.logspace(), 318
np.mean(), 47, 176
np.nan, 60
np.nanmean(), 541
np.percentile(), 228
np.power(), 219
np.random.choice(), 553
np.random.default_rng(), 46,
47
np.random.normal(), 45
np.sqrt(), 45np.squeeze(), 457 np.std(), 47 np.sum(), 43 np.var(), 47 np.where(), 180 ns(), 317 numpy, 42, 555 os.chdir(), 55 outer(), 219 pairwise_distances(), 554 pairwise_tukeyhsd(), 587 pandas, 55 params, 175 partial(), 222, 269 PCA(), 280, 537, 540, 554 pd, see pandas pd.crosstab(), 555 pd.cut(), 315 pd.get_dummies(), 314 pd.plotting.scatter_matrix(), 62 pd.qcut(), 314, 315 pd.read_csv(), 55, 556 pd.Series(), 62 Pipeline(), 275 plot(), 48, 61, 356, 490 plot.scatter(), 120 plot_gam(), 321 plot_svm(), 398 PLSRegression(), 282 poly(), 125, 313, 327 predict(), 175, 178, 181, 216, 218, 323, 358 predict_survival_function(), 493 print(), 40 pvalues, 175 pygam, 307, 317 pytorch_lightning, 435 QDA(), see QuadraticDiscriminant-Analysis() QuadraticDiscriminantAnalysis(), 174, 181 random(), 555 RandomForestRegressor(), 354, 360 read_image(), 436 reindex(), 461 reshape(), 43
return, 198
RF(), see RandomForestRegressor()
rng, see np.random.default_rng()
rng.choice(), 60
rng.standard_normal(), 60
roc_curve(), 392
RocCurveDisplay.from_estimator(),
387
savefig(), 50
scatter(), 49, 61
scipy.interpolate, 315
score(), 218, 461
seed_everything(), 436
set_index(), 57
set_title(), 49
set_xlabel(), 49
set_xscale(), 198
set_ylabel(), 49
set_yscale(), 198
shape, 43
ShuffleSplit(), 219
sim_time(), 495
SimpleDataModule(), 441
SimpleModule.classification(),
446
SimpleModule.regression(),
442
skl, see sklearn.linear_model
skl.ElasticNet(), 273, 277
skl.ElasticNet.path, 274
skl.ElasticNet.path(), 273
sklearn, 118, 181
sklearn.ensemble, 360
sklearn.linear_model, 267
sklearn.model_selection, 267
sklearn_selected(), 269
sklearn_selection_path(),
270
sklearn_sm(), 218
skm, see sklearn.model_selection
skm.cross_val_predict(), 271
skm.KFold(), 271
skm.ShuffleSplit(), 272
slice(), 51, 462
sm, see statsmodels
sm.GLM(), 174, 192, 226
sm.Logit(), 174
sm.OLS(), 118, 129, 174, 319StandardScaler(), 185, 438,
537, 555
statsmodels, 116, 173
std(), 186
Stepwise(), 269
str.contains(), 59
subplots(), 48
sum(), 43, 268
summarize(), 118, 129, 223,
226
summary(), 119, 322, 587
super(), 440
SupportVectorClassifier(),
387, 389–391, 393
SupportVectorRegression(),
394
SVC(), see SupportVector-
Classifier()
svd(), 539
SVR(), see SupportVector-
Regression()
TensorDataset(), 441
to_numpy(), 437
torch, 435
torchinfo, 436
torchmetrics, 436
torchvision, 436
ToTensor(), 444
train_test_split(), 186, 216
transform(), 118, 119
ttest_1samp(), 584
ttest_ind(), 590
ttest_rel(), 587
tuple, 43
uniform(), 555
value_counts(), 66
var(), 536
variance_inflation_factor(),
116, 124
VIF(), see variance_inflation-
_factor()
where(), 355
zip(), 60, 312q-values, 589 quadratic, 98 quadratic discriminant analysis, 4, 135, 156–157, 164–167
qualitative, 2, 27, 91, 135, 167, 202 variable, 91–94 quantitative, 2, 27, 91, 135, 167, 202 radial kernel, 381, 383, 390 random forest, 11, 331, 343, 346– 347, 354, 360–361 random seed, 46 re-sampling, 577–582 recall, 155 receiver operating characteristic (ROC), 154, 382–383 recommender systems, 516 rectifed linear unit, 401 recurrent neural network, 416–427 recursive binary splitting, 334, 337, 338 reducible error, 17, 90 regression, 2, 11, 27 local, 289, 290, 304–305 piecewise polynomial, 294–295 polynomial, 289–292, 299 spline, 289, 294 tree, 331–337, 358–360 regularization, 230, 240, 406, 484– 486 ReLU, 401 resampling, 201–214 residual, 71, 81 plot, 100 standard error, 75, 77–78, 88– 89, 109 studentized, 104 sum of squares, 71, 79, 81 residuals, 263, 348 response, 15 ridge regression, 11, 240–244, 385, 484 risk set, 473 robust, 374, 376, 535 ROC curve, 154, 382–383, 486– 487 R2, 77–80, 88, 109, 238 rug plot, 314 scale equivariant, 242 Schefé’s method, 572 scree plot, 512, 514–515
elbow, 514 semi-supervised learning, 27 sensitivity, 153, 155, 156 separating hyperplane, 367–372 Seq2Seq, 425 sequence, 41 shrinkage, 230, 240, 484–486 penalty, 240 sigmoid, 401 signal, 252 signature, 45 singular value decomposition, 539 slack variable, 375 slice, 51 slope, 71, 72 Smarket data set, 2, 3, 12, 173, 184, 196 smoother, 308 smoothing spline, 290, 300–303 soft margin classifer, 372–374 soft-thresholding, 250 softmax, 145, 405 sparse, 244, 252 sparse matrix format, 414 sparsity, 244 specifcity, 153, 155, 156 spline, 289, 294–303 cubic, 296 linear, 296 natural, 297, 301 regression, 289, 294–299 smoothing, 30, 290, 300–303 thin-plate, 22 standard error, 75, 101 standardize, 185 statistical model, 1 step function, 111, 289, 292–293 stepwise model selection, 11, 231, 233 stochastic gradient descent, 429 string, 41 string interpolation, 490 stump, 349 subset selection, 230–240 subtree, 336 supervised learning, 25–27, 261 support vector, 371, 376, 385 classifer, 367, 372–377 machine, 5, 11, 24, 377–386
regression, 386 survival analysis, 469–502 curve, 472, 483 function, 472 time, 470 synergy, 70, 89, 95–98, 110–111 systematic, 16 t-distribution, 77, 165 t-statistic, 76 t-test one-sample, 583, 584, 588 paired, 587 two-sample, 559, 570, 571, 577– 581, 584, 590 test error, 35, 37, 176 MSE, 28–32 observations, 28 set, 30 statistic, 559 theoretical null distribution, 577 time series, 101 total sum of squares, 79 tracking, 102 train, 21 training data, 20 error, 35, 37, 176 MSE, 28–31 transformer, 311 tree, 331–342 tree-based method, 331 true negative, 155 true positive, 155 true positive rate, 155, 156, 382 truncated power basis, 296 Tukey’s method, 571, 585, 587 tuning parameter, 187, 240, 484 two-sample t-test, 474 Type I error, 155, 562–565 Type I error rate, 563 Type II error, 155, 563, 568, 584
unsupervised learning, 25–27, 255, 260, 503–552 USArrests data set, 12, 507, 508, 510, 512, 513, 515, 516, 518, 519 validation set, 202 approach, 202–204 variable, 15 dependent, 15 dummy, 91–94, 97–98 importance, 346, 360 independent, 15 indicator, 35 input, 15 output, 15 qualitative, 91–94, 97–98 selection, 86, 230, 244 variance, 18, 31–34, 159 infation factor, 108–110, 123 varying coefcient model, 305 Wage data set, 1, 2, 8, 9, 12, 290, 291, 293, 295, 297–300, 302–306, 309, 315, 327 weak learner, 343 weakest link pruning, 336 Weekly data set, 12, 196, 226 weight freezing, 412, 419 weight sharing, 418 weighted least squares, 103, 304 weights, 404 with replacement, 214 within class covariance, 150 wrapper, 217